

“The papers of Aristotle had suffered grievously and were in places illegible; but Apellicon occupied himself with copying and editing them. Tyrannion found that the editing of Apellicon was excessively bad. Ultimately, the peripatetic scholiarch Andronicus of Rhodes undertook the arrangement of the papers, the correction of the text, and the publication of the new edition.”
The papers of Charles Peirce may not have not suffered as grievously from damp and insects as those of Aristotle, but their general state of disorganization and partial subjection to arbitrary editing have long required peripatetic editors to undertake their arrangement and their correction in order to publish them in a new edition. Extensive information regarding the methods followed to produce the edition is given under the Methods tab.
As a selective but comprehensive chronological and critical edition, the Writings of Charles S. Peirce covers the full range of Peirce’s published and unpublished texts on any subject in a chronological sequence that reveals his often simultaneous work across many fields of study. Larger sequences of writings are grouped together within a volume if they represent a fairly concentrated period of work. The need for a chronological edition is especially strong in Peirce’s case; earlier editions were either topical or limited to a small selection of works, and provided little sense of his evolving thought or sufficient context for the massive body of his unpublished writings.
The core of the edition consists of several components:
“This new edition of Berkeley’s works is much superior to any of the former ones. It contains some writings not in any of the other editions, and the rest are given with a more carefully edited text. The editor has done his work well. The introductions to the several pieces contain analyses of their contents which will be found of the greatest service to the reader.”
This two-volume chronological edition makes available a comprehensive selection of Peirce’s most seminal philosophical writings. All the texts included are classics that will continue to influence the way philosophers think for centuries to come.
Work on this edition began in 1991 when Nathan Houser and Christian Kloesel agreed to prepare a two-volume collection of Peirce’s philosophical volumes suitable for university seminars. Houser and Kloesel completed Volume 1 in 1992 and made a preliminary selection for Volume 2, but were unable to carry that work through to completion. In January 1997, the Peirce Edition Project agreed to finish the selection and to undertake the editing for Volume 2. It appeared in the spring of 1998. Royalties for both volumes have been assigned to the Peirce Edition Project.
Volume 1 presents twenty-five key texts, chronologically arranged, beginning with Peirce’s “On a New List of Categories” of 1867, a groundbreaking historical alternative to Kantian philosophy, and ending with the first sustained and systematic presentation of his evolutionary metaphysics in the Monist Metaphysical Series of 1891-1893. The book features a clear introduction and informative headnotes to help readers grasp the nature and significance of Peirce’s systematic philosophy and its development.
Volume 2 provides the first comprehensive anthology of Peirce’s mature philosophy. During his later years Peirce worked unremittingly to integrate new insights and discoveries into his general system of philosophy and to make his major doctrines fully coherent within that system. A central focus of Volume 2 is Peirce’s evolving theory of signs and its application to pragmatism. Included are 31 pivotal texts, beginning with “Immortality in the Light of Synechism” (in which Peirce proposes synechism—the tendency to regard everything as continuous—as a key advance over materialism, idealism, and dualism) and ending with Peirce’s late and unfinished investigations of the relative merits of different kinds of reasoning. Peirce’s Harvard Lectures on Pragmatism and selections from A Syllabus of Certain Topics of Logic are among the texts included.
“To explain is to show the unity at the heart of the manifold.”
Volume 1 takes up Peirce’s early years and presents the seminal writings that laid the groundwork for Peirce’s future studies in logic and the sign theory of cognition.
The volume opens with a sampling of the more philosophical compositions Peirce wrote during his last three years at Harvard College, from 1857 to 1859—essays that reveal a variety of nascent themes being explored by a precocious young man busy initiating himself to the methods of logical argumentation and rigorous expression while reading such works as Schiller’s Aesthetic Letters and Kant’s Critique of Pure Reason. Beneath his exploration of esthetic, moral, and psychological topics, Peirce already manifests a penchant for working out the logical structures that underlie them. This includes especially his attempts to improve upon and extend Kant’s list of categories. His assiduous reading of Kant, tempered by his father Benjamin’s prodding questions and by his own training in scientific reasoning (as in chemistry) and his growing experience in field research, turns Peirce into a metaphysician eager to transcend at once transcendentalism (an abuse of psychology), rationalism (an abuse of logic), and dialectics (an abuse of dogmatism) thanks to the adoption of a trusting fideism that does not seek to justify what needs no critical justification nor seeks to doubt what needs no skeptical dismissal. Such philosophical growth occurs notably in the 1861–62 “Treatise on Metaphysics,” a daring piece of innovative speculation for a thinker in his early twenties.
The core of Volume 1 consists of two series of lectures: the nine extant Harvard Lectures of February-May 1865 on “The Logic of Science,” and the ten extant Lowell Lectures of September–November 1866 on “The Logic of Science; or Induction and Hypothesis.” Those sets of lectures exhibit a broadening command of the history of logic and philosophy.
Already well read in Aristotle’s major works, Peirce in the Harvard Lectures shows familiarity with the major thinkers of the modern period and has begun reading medieval treatises in logic with uncommon interest. Right away Peirce militates in favor of an “unpsychological view of logic” and argues powerfully about the advantages of doing so, partly on the basis of fundamentally semiotic considerations. He studies the intricacies of the interplay between extension and comprehension and their connection with different types of signs and syllogistic reasoning. He shares his cutting-edge forays into Boolean algebra and illustrates the benefits of its symbolical notation for the analysis of intricate propositions, quantified or not. He studies induction with the help of Whewell, Mill, and Comte, and identifies the insufficiencies of their positions. He turns back to Kant and grapples with the distinction between analytic and synthetic judgments, and between a priori and a posteriori knowledge. And he puzzles again about Kant’s table of the functions of judgment and criticizes them on the basis of new logical distinctions. The last Harvard lectures see Peirce return to induction, and also to hypothesis, and display multiple analyses of those inferences in a syllogistic context as well as from the standpoint of the logical quantity of propositions. A definite trichotomic method gets deeply rooted in those lectures, a direct consequence of Peirce’s natural attraction to the fundamental patterns of logical structures.
Many texts at the center of Volume 1 help trace out Peirce’s progress in framing a new theory of categories, a theory that sees him both redefine the very notion of category and work out the logical methodology in identifying and testing any concept that would be a candidate for such an elementary status among conceptions. Especially striking is Peirce’s early conviction that the method that discovers categories cannot be deductive, a priori, or transcendental, but must be inductive. Equally fascinating is his framing the categories as the fundamental logical steps that govern the passage from substance to being, a passage that can only be made out by navigating it back from being to substance.
In the Lowell Lectures, Peirce reprises all the themes of his Harvard Lectures, taking advantage of one year and a half of considerable further reading and logical research. He classifies all the forms of deductive reasoning and takes up Aristotelian and Theophrastean syllogisms. He tests the extent to which syllogistic can accommodate relative predicates and mathematical demonstrations. He returns to induction, but now explores it in the context of the calculus of probabilities, and also in the context of a criticism of J. S. Mill’s conception of the uniformity of nature. He develops his information theory based on both the multiplication of the extension and comprehension of a proposition and on the conception of the interpretant as an equivalent representation. He presents publicly for the first time (in the non-extant lecture 8) his new list of three categories (within the passage from substance to being), and returns to it in the ninth lecture in considerable detail. And he vividly suggests how logic can apply to metaphysics.
The volume closes with Peirce’s important “Memoranda Concerning the Aristotelean Syllogism,” in which he demonstrates that no syllogism of the second or third figure can be reduced to the first figure, and with [“On a Method of Searching for the Categories”], the most extensive (and illuminating) draft of the 1867 essay “On a New List of Categories.”
“A certain child who is rather backward in learning to speak . . . has got to use three words only; and what are these? Name, story, and matter. . . . Already he has made his list of categories, which is the principal part of any philosophy.”
| Preface | xi |
| Acknowledgments | xiv |
| Introduction |
xv |
| 1. My Life written for the Class-Book | 1 |
| 2. Private Thoughts principally on the conduct of life | 4 |
| 3. The Sense of Beauty never furthered the Performance of a single Act of Duty | 10 |
| 4. Raphael and Michael Angelo compared as men | 13 |
| 5. A Scientific book of Synonyms | 17 |
| 6. Think Again! | 20 |
| 7. Analysis of Genius | 25 |
| 8. The Axioms of Intuition. After Kant | 31 |
|
THREE ESSAYS ON INFINITY AND GOD |
|
| 9. An essay on the Limits of Religious thought written to prove that we can reason upon the nature of God | 37 |
| 10. [The Conception of Infinity] | 40 |
| 11. Why we can Reason on the Infinite | 42 |
| 12. Proof of the Infinite Nature of the Creator | 44 |
| 13. I, IT, and THOU: A book giving Instruction in some of the Elements of Thought | 45 |
| 14. The Modus of the IT | 47 |
| 15. Views of Chemistry: sketched for Young Ladies | 50 |
| 16. [A Treatise on Metaphysics] | 57 |
| 17. Analysis of Creation | 85 |
| 18. S P Q R | 91 |
| 19. The Chemical Theory of Interpenetration | 95 |
| 20. [The Place of Our Age in the History of Civilization] | 101 |
| 21. Letter Draft, Peirce to Pliny Earle Chase | 115 |
| 22. [Shakespearian Pronunciation] | 117 |
| 23. Analysis of the Ego | 144 |
| 24. A Treatise of the Major Premisses of Natural Science | 152 |
| 25. On the Doctrine of Immediate Perception | 153 |
| 26. Letter, Peirce to Francis E. Abbot | 156 |
|
ON THE LOGIC OF SCIENCE [HARVARD LECTURES OF 1865] |
|
| 27. Lecture I | 162 |
| 28. Lecture II | 175 |
| 29. Lecture III | 189 |
| 30. Lecture on the Theories of Whewell, Mill, and Compte | 205 |
| 31. Lecture VI: Boole's Calculus of Logic | 223 |
| 32. Lecture on Kant | 240 |
| 33. Lecture VIII: Forms of Induction and Hypothesis | 256 |
| 34. Lecture X: Grounds of Induction | 272 |
| 35. Lecture XI | 286 |
| 36. Teleological Logic | 303 |
| 37. An Unpsychological View of Logic to which are appended some applications of the theory to Psychology and other subjects | 305 |
| 38. Logic of the Sciences | 322 |
| 39. [The Logic Notebook] | 337 |
| 40. Logic Chapter I | 351 |
|
THE LOGIC OF SCIENCE; OR, INDUCTION AND HYPOTHESIS [LOWELL LECTURES OF 1866] |
|
| 41. Lecture I | 358 |
| 42. Lecture II | 376 |
| 43. Lecture III | 393 |
| 44. Lecture IV | 407 |
| 45. Lecture V | 423 |
| 46. [Lecture VI] | 440 |
| 47. Lecture VII | 454 |
| 48. Lecture IX | 471 |
| 49. Lecture X | 488 |
| 50. Lecture XI | 490 |
| 51. Memoranda Concerning the Aristotelean Syllogism | 505 |
| 52. [On a Method of Searching for the Categories] | 515 |
|
APPENDIX |
|
| 53. [Diagram of the IT] | 530 |
| Editorial Notes | 531 |
| Bibliography of Peirce’s References | 564 |
| Chronological List, 1849-1866 | 569 |
| Essay on Editorial Method | 578 |
| Explanation of Symbols | 586 |
| Textual Notes | 588 |
| Emendations | 591 |
| Word Division | 685 |
| Index | 688 |
When Peirce graduated from Harvard College in 1859, he was not yet twenty. Shortly before graduation, each member of his class wrote an entry in the Harvard Class Book of 1859. Peirce’s was a humorous autobiography-in-miniature, with a sub-entry for each of the years from 1839 through 1859. The last was: "1859. Wondered what I would do in life." In a private notebook, "My Life written for the Class-Book" is continued through 1861. The last sub-entry reads: "1861. No longer wondered what I would do in life but defined my object." What was the reason for the wonder of 1859, and what had happened by 1861 to dispel that wonder and define the object?
In the male line, Peirce was descended from a John Pers (ca. 1588-1661) who came from Norwich, England, in 1637, and settled in Watertown, Massachusetts. For four generations, the Peirces were craftsmen, shopkeepers, or farmers. Then Jerathmiel (1747-1827) married Sarah Ropes, settled in Salem, entered the East India shipping trade, prospered, and built the elegant Peirce-Nichols house at 80 Federal Street. His son Benjamin (1778-1831) graduated from Harvard College, married Lydia Ropes Nichols, entered the shipping trade with his father, became a state senator, and, when Salem's shipping trade declined, became Librarian at Harvard, published a four-volume Catalogue of the library's holdings, and wrote a history of the university, which was published shortly after his death. His son Benjamin (1809-1880) graduated from Harvard College in 1829, taught for a time at the Round Hill School at Northampton, Massachusetts, and married Sarah Hunt Mills, daughter of Elijah Hunt Mills, a lawyer, co-founder of a law school there, and immediate predecessor of Daniel Webster as United States senator from Massachusetts. This Benjamin Peirce, father of our Charles S. Peirce, became professor of astronomy and mathematics at Harvard, and was the leading American mathematician of his day. He was active in the Lazzaroni, an informal group of "beggars" for federal support of scientific research, and in the movement for a national university. He published several mathematical textbooks of high quality. His major works were Analytic Mechanics (1855-57) and Linear Associative Algebra (1870). He was president of the American Association for the Advancement of Science in 1853-54, and one of the founders of the National Academy of Sciences in 1863. Just beyond our period, he was superintendent of the U. S. Coast Survey from 1867 to 1874. His brother Charles Henry Peirce was a physician, and his sister Charlotte Elizabeth Peirce had kept school and taught privately, and was at home in German and French literature.
A sister of Benjamin Peirce’s wife married Charles Henry Davis, who after seventeen years in the Navy (1823-1840) took up residence in Cambridge, studied mathematics with Benjamin, joined the Coast Survey, and in 1849 became the first superintendent of the American Ephemeris and Nautical Almanac.
Benjamin and Sarah had five children: James Mills (1834-1906), Charles Sanders (1839-1914), Benjamin Mills (1844-1870), Helen Huntington (1845-1923), and Herbert Henry Davis (1849-1916). James Mills (Jem), after graduating from Harvard in 1853, spent a year in the Law School, was tutor in mathematics for several years, graduated from the Divinity School in 1859, spent two years in the ministry, returned to the teaching of mathematics, and eventually succeeded to his father's professorship. Benjamin Mills, after graduating from Harvard in 1865, studied at the Paris School of Mines and later at the Lawrence Scientific School, became a mining engineer, and compiled A Report on the Resources of Iceland and Greenland, which was published by the U.S. State Department in 1868; but he died early in 1870 at Ishpeming in northern Michigan. Helen married William Rogers Ellis, who went into the rolling mill business and eventually into real estate. Herbert, after some years in the interior decorating and other businesses, became a diplomat, was secretary of legation at the U.S. embassy in St. Petersburg, then Third Assistant Secretary of State, and later minister to Norway.
The full range of the learned professions of law, medicine, divinity, and higher education, as well as business, engineering, politics, and diplomacy, was represented in the immediate family or by near relatives. Literature, the theater, and other arts were cherished if not represented. Benjamin Peirce, Charles's father, was a member of the Saturday Club, along with Emerson, Longfellow, Lowell, Oliver Wendell Holmes, and other literary figures. The Peirces were devotees of the theater, attended plays in Boston, and entertained actors in their home. Amateur theatricals were a common form of home entertainment. But what stood out for Charles in looking back from later years was that he had grown up in the Cambridge "scientific circle." The biologist and geologist Louis Agassiz lived but a stone's throw from the Peirces, and was a frequent visitor. Peirce, Agassiz, and Davis were leading members of the Cambridge Scientific Club. That club had at least fifteen meetings in the Peirce home before Charles defined his object, and another five during the years 1861-66. The Cambridge Astronomical Society (1854-57), which met every two weeks, began with Benjamin Peirce as president and Joseph Winlock as recording secretary. It was succeeded by a Mathematics Club presided over by Benjamin Peirce, which met on Wednesday afternoons for several years. It was attended by all the members of the Nautical Almanac staff. To that club Charles himself presented a paper on the four-color problem in the 1860s.
The items in the Class Book entry that shed most light on Charles's intellectual development are all extra-curricular: (1) "taking up the subject of Chemistry" (1847); (2) "Wrote a 'History of Chemistry'" (1850); (3) "Worked at Mathematics for about six months" (1854); (4) "Read Schiller's AEsthetic Letters and began the study of Kant" (1855).
We begin where Charles began, with chemistry. His father was one of the moving spirits behind the establishment within Harvard University of the Lawrence Scientific School in 1847. Eben Norton Horsford had then recently returned from two years at Giessen studying chemistry under Liebig, who combined laboratory instruction with demonstration experiments during lectures. To Liebig more than to anybody else it was due that the experimental method of teaching was more highly developed in chemistry than in any other science, so that the study of chemistry offered at that time the best entry into experimental science in general. Horsford was now made professor of chemistry in the Lawrence Scientific School, where he established, on the Liebig model, the first laboratory in America for analytical chemistry. Charles's uncle, Charles Henry Peirce, until then a practicing physician in Salem, became Horsford's assistant and was encouraged by him to translate Stockhardt's Die Schule der Chemie for textbook use. Charles's aunt, Charlotte Elizabeth Peirce, whose German was excellent, did most of the actual work of translation. During the years in which the chemical laboratory was being established and the translation was in progress, Charles's uncle and aunt helped him set up a private laboratory at home and work his way through Liebig's hundred bottles of qualitative analysis. In 1850, when the translation appeared, Charles, then eleven, wrote a "History of Chemistry" (which has not been found) . In the same year, his uncle became federal inspector of drugs for the port of Boston, and two years later, in 1852, published Examinations of Drugs, Medicines, Chemicals, Etc., as to their Purity and Adulterations, giving some of the results of his official labors. Not long before Charles entered Harvard College in 1855, his uncle died, and Charles inherited his chemical and medical library. Charles's college teacher of chemistry was Josiah P. Cooke, the initiator of laboratory instruction at the undergraduate level. The textbook he used was Stockhardt's, as translated by Charles's aunt and uncle under the title Principles of Chemistry, Illustrated by Simple Experiments.
One episode not recorded in his Class Book entry, but more often recalled in later life than any that is recorded there, was that of his introduction to logic, within a week or two of his twelfth birthday, in 1851. His older brother Jem was about to enter upon his junior year at Harvard College and had bought his textbooks for the year. Among them was Whately's Elements of Logic. Charles dropped into Jem's room, picked up the Whately, asked what logic was, got a simple answer, stretched himself on the carpet with the book open before him, and over a period of several days absorbed its contents. Since that time, he often said late in life, it had never been possible for him to think of anything, including even chemistry, except as an exercise in logic. And so far as he knew, he was the only man since the Middle Ages who had completely devoted his life to logic.
In his freshman year at college, Charles began intensive private study of philosophy with Schiller's Aesthetic Letters. From that he moved on to Kant's Critic of the Pure Reason. In his later college years, while continuing with Kant, he added modern British philosophy. In his junior year, he had to recite on Whately's Elements of Logic, as Jem had done six years before him. But all the while, as he later said, he "retained . . . a decided preference for chemistry," and it was taken for granted in the family that he was headed for a career in that science. The obvious next step after graduating would have been to enter the Lawrence Scientific School. But he felt the need of experience at earning his own living, and he had suffered so from ill health during his senior year that an interval of outdoor employment in science seemed desirable before he proceeded further. His father's friend, Alexander Dallas Bache, superintendent of the Coast Survey, offered him a place in his own field party in Maine in the fall of 1859, and in another field party around the delta of the Mississippi in the winter and spring of 1860. In early August 1859, before joining Bache's party, Charles spent a week at Springfield reporting sessions of the American Association for the Advancement of Science for six issues of the Boston Daily Evening Traveler.
On 18 December 1859 Charles wrote Jem, who was then a minister, a long letter from Pascagoula, Mississippi, in which he sought Jem's counsel. A man's first business, thought Charles, is to earn a living for himself—and for his family if he has any. Scientific research is for such leisure as that may leave him; society cannot be expected to pay for what it may have for nothing. It would appear, then, that his wondering in the Class Book what he would do in life meant wondering how he would earn a living, whether he would marry, what leisure he would have for science and for the logic of science. Jem replied at great length on 10 January. Society does pay for science, he wrote, at least if the scientific man has a practical side to his profession. And if one has a strong preference for science one will never be happy in any other occupation. "I have often thought what a fine thing it would be if you & Benjy & I should go into different departments of science: Chemistry, Natural History, & Mathematics."
During Charles's absence in Maine and Louisiana, Darwin's Origin of Species appeared, and also a separate edition of Agassiz's Essay on Classification. Chemistry was an experimental but also a classificatory science. Biology was the chief other classificatory science. The differences between these two sciences were being brought into focus by the controversy between supporters of Darwin and supporters of Agassiz. In the latter half of 1860, while serving as proctor and tutor at Harvard College, Charles was for six months a private student of Agassiz's, to learn his method of classification. One of the tasks that Agassiz set him was sorting out fossil brachiopods.
In the spring of 1861 Charles at last entered the Lawrence Scientific School. Two and a half years later he graduated as a summa cum laude Bachelor of Science in Chemistry. But during his first term the Civil War had begun, and his father had lost, by resignation, the computing aide who assisted him in his chief service to the Coast Survey, that of determining the longitudes of American in relation to European stations from occultations of the Pleiades by the moon. Charles asked his father to obtain that appointment for him. His father wrote Superintendent Bache that he had at first urged his son to "keep to his profession and wait until he could get money by his chemistry—to which he replied that he wants to get the means to buy books and apparatus and devote himself longer to the study of his profession." Bache authorized Charles's appointment as aide beginning 1 July 1861, and he was launched on the career that occupied his next thirty and a half years and took him from chemistry into astronomy, geodesy, metrology, spectroscopy, and other sciences. Some measure of his attainments in them may be found in the facts that his father proposed him for the chair of physics at The Johns Hopkins University to which Henry Augustus Rowland was appointed, and that he was the first modern experimental psychologist on the American continent.
Throughout those thirty and a half years and on beyond them, however, when he had occasion to state his profession, or even his occupation, he continued to call himself a chemist. His first professional publication, in 1863 at the age of twenty-three, was on "The Chemical Theory of Interpenetration." In later years he found in Mendeleev's work on the periodic law and table of the elements the most complete illustration of the methods of inductive science. And he took satisfaction in having, in June 1869, when he was not yet thirty, published a table of the elements that went far in Mendeleev's direction, before Mendeleev's announcement of the law, a little earlier in the same year, became known in western Europe and America. At that year's meeting of the American Association for the Advancement of Science it was remarked that Peirce "had greatly added to the illustration of the fact of pairing by representing in a diagram the elements in positions determined by ordinates representing the atomic numbers."
At the end of 1891, after thirty-one and a half years in the service of the Coast and Geodetic Survey, his appointment was terminated, and he set up in private practice as a chemical engineer, thereby returning to the profession to which he had committed himself before he entered the Survey, and from which his career in the Survey had been in some sense a diversion.
It was not until 1906, in the first edition of American Men of Science, that for the first time in any biographical reference work, logic was named as the chief field of his investigations. In the first five editions of Who's Who in America, from 1899-1900 through 1908-1909, his profession appears as that of lecturer and engineer. In the sixth edition, that of 1910-1911, for the first time in any reference work, it appears as that of logician. Only after his death did he begin to be called a philosopher.
How then had he defined his object when in 1861 he no longer wondered what he would do in life? There are no letters or other records of that year from which an explicit, complete, and confident answer can be drawn. We are reduced therefore to piecing together the few indications we have from that time, and filling them out from subsequent events and from Peirce’s later recollections and autobiographical remarks.
Chemistry at that time offered the best entry into experimental science in general, and was therefore the best field in which to do one's postgraduate work, even if one intended to move on to other sciences and, by way of the sciences, to the logic of science and to logic as a whole. Moreover, chemical engineering was then the most promising field in which to make a living by science, if one had no opportunity to do so by pure science or by logic.
That Peirce had no intention of confining himself to chemistry appears from his spending six months in private study of zoological classification under Agassiz before entering the Lawrence Scientific School. It appears also from his oration on "The Place of Our Age in the History of Civilization" (1863) and from "Shakespearian Pronunciation" (1864). It becomes fully evident from the two courses of lectures on the logic of science which he delivered in the spring of 1865 and the fall of 1866, and from the course on the history of logic in Great Britain which he delivered in 1869-70. The first and third of these courses were "University Lectures" at Harvard, each a part of an extensive program of such courses intended primarily for graduates of the college, and each offered but once. One of the men who attended the third course, along with others given in 1869-70, described them many years later as "The Germ of the Graduate School." Both in the university and in the Lowell Institute, in which the second course was given, each lecturer was expected to devote his lectures to the field and topics of his greatest competence, or on which he had most to offer that was new.
The most striking evidence, however, may be found in Peirce’s election in January 1867 to the American Academy of Arts and Sciences, and in April 1877 to the National Academy of Sciences. To the former academy, in March, April, May, September, and November 1867 he presented five papers, all in logic, and all his subsequent papers in the Proceedings and Memoirs of that academy were in logic. Before his election to the National Academy, he was asked to send a list of his scientific papers, but sent instead the titles of four of his papers in logic and said he wished to be judged by those alone; and after his election he wrote to the secretary expressing his gratification at the implied recognition of logic as a science. Of the thirty-four papers he presented to the National Academy from 1878 to 1911, nearly a third were in logic. Others were in mathematics, physics, geodesy, spectroscopy, and experimental psychology; but in none of these fields did the number approach that in logic.
In connection with Peirce’s private study of zoological classification under Agassiz, we mentioned that biology, like chemistry, is a classificatory science. We may add now that logic also is a classificatory science; that in Peirce’s first series of published papers in logic, which will appear early in our second volume, the second paper was called "On a Natural Classification of Arguments"; that his first privately printed paper in logic, his "Memoranda Concerning the Aristotelean Syllogism," near the end of the present volume, contained his first original contribution to the classification of arguments; that he at that time conceived logic to be a branch of semeiotic, the general theory of signs; that he later adopted a much broader conception of logic in which, if it was not coextensive with semeiotic, it was so nearly so that for some time to come logicians were likely to be the chief cultivators of the general theory of signs; and that, in his own lifetime as a whole, he devoted more labor to the classification of signs than to any other single field of research. His pragmatism, for example, lay wholly within its scope.
How then had Peirce defined his object in 1861? Somewhat as follows, we may safely infer from all the evidence, early and late. In mathematics and in as wide a range of the sciences, physical and psychical, as possible—including the history of science and of mathematics—he would reach the point of carrying out and publishing original researches. He would begin with chemistry, the open sesame to the experimental sciences. He would earn his living by science as far as possible, so that his hours of employment as well as of leisure should further his object. He would prefer employment that gave him scope for diversity of researches over a period of years. His researches in sciences other than logic would in the first place be for the sake of those sciences themselves, but all would be brought to a second focus in logic, as including both the logic of mathematics and the logic of science, and eventually as including the general theory of signs. By bringing logic (and thereby metaphysics) abreast of the exact sciences in which he had been bred, he would at the same time serve the several sciences at a second and higher level.
But why should Peirce have supposed that by first making positive contributions to mathematics and to a wide range of the sciences he would then become a better contributor to logic? Because a scientific logic must take full account of the reasonings of mathematics and the sciences and because the traditional logic has failed to do so. It has failed in part because mathematicians who are not logicians, and logicians who are not mathematicians, are not fully competent to analyze the reasonings of mathematicians; and because scientists who are not logicians, and logicians who are not scientists, or who are scientists in only a single science or in but two or three closely related sciences, are not fully competent to analyze the reasonings of scientists.
If we think of the literature of the logic of science as including on the one hand Descartes's Discourse on the Method of Rightly Conducting the Reason and Searching for the Truth in the Sciences; and on the other Bacon's Novum Organum and Whewell's Novum Organon Renovatum it will seem at least an hypothesis worth trying that a logician's ability to contribute to the logic of science may be enhanced by extending the range of his scientific researches. For Whewell had done just that, and had also written and published a three-volume History of the Inductive Sciences (1837), before publishing his two-volume Philosophy of the Inductive Sciences, Founded Upon Their History (1840). His Novum Organon Renovatum (1858) was Part 2 of the third edition of the latter work.
In his 1865 Harvard University Lectures on the Logic of Science, in the present volume, Peirce speaks of Whewell as "man of science," "historian of science," and "the most profound writer upon our subject." But he speaks at much greater length in the lecture on Whewell in his Harvard University Lectures of 1869 on the British Logicians, which will appear in volume 2. That may be our best evidence of the way in which Peirce had defined his object in life.
But whether in fact, and to what extent, Peirce’s contributions to the logic of science can be traced to the diversification of his scientific researches is still to be determined, and it is one of the aims of the present edition of his writings to open the way toward answering that question .
When Bacon gave the title Novum Organum to the second part of his major work, The Great Instauration, and when Whewell gave the title Novum Organon Renovatum to the second part of his major work in its third edition, they thereby claimed to be making great advances in logic, the science founded by Aristotle in his Organon Advances not in the whole range of the Organon, to be sure, but only in the logic of science; more exactly, in the theory of how the inductive and especially the experimental sciences are advanced. But the Organon itself began with a treatise on Categories, in which ten were listed and discussed; and Peirce began where the Organon began.
Aristotle's categories were substance, quantity, quality, relation, place, time, position, state, action, and passion. Many lists differing more or less from his were drawn up by later logicians. In Peirce’s time the best known of these were Kant's short list of twelve and the long list of Hegel's Encyclopedia of the Philosophical Sciences. Bacon had used the phrase "Transcendentals, or Adventitious Conditions of Essences." Whewell used the phrase "Fundamental Ideas" but offered no inclusive list; it was for the future progress of the sciences to evolve one.
Looking back from 1898, Peirce wrote: "In the early sixties I was a passionate devotee of Kant, at least as regards the Transcendental Analytic in the Critic of the Pure Reason. I believed more implicitly in the two tables of the Functions of Judgment and the Categories than if they had been brought down from Sinai." In Meiklejohn's translation of 1855, which Peirce owned and used beginning not later than 1856, the two tables appear six pages apart. To facilitate comparison, we present them here in parallel columns.
[TABLE OF JUDGMENTS]
I. Quantity of judgments
Universal
II. Quality
Affirmative
III. Relation
Categorical
IV. Modality
Problematical
TABLE OF THE CATEGORIES
I. Of Quantity
Unity
II. Of Quality
Reality
Of Inherence and Subsistence (substantia et accidens)
IV. Of Modality
Possibility-Impossibility
For the present we shall confine our attention to the Table of the Categories. It is obvious at once that three of Aristotle's ten categories appear as heads of three of Kant's four triads, and two or three others appear in modified forms within them. Hegel remarked that the four headings that Kant used for his triads were in fact categories of a more general nature. Kant himself had remarked that in each triad the third category arises from the combination of the second with the first. Peirce will later make a similar observation about Hegel's three stages of thought, which he will call Hegel's universal categories, as distinguished from the particular categories of the Encyclopedia. He will also say that his own three categories correspond both to Hegel's universal categories and to the three categories implicit in each of Kant's four triads.
Volume 2 will include the five papers in logic that Peirce presented to the American Academy of Arts and Sciences in 1867. The third of them offered the following "New List of Categories:
BEING,
Quality
(Reference to a Ground),
Relation
(Reference to a Correlate),
Representation (Reference to an
Interpretant),
SUBSTANCE.
Peirce soon reduced the five to three by sloughing off Being and Substance. We note at once that two of Aristotle's categories reappear in Peirce’s triad as well as in the headings of two of Kant's triads. Only representation is new. But that is novelty enough. It is the first list of categories that opens the way to making the general theory of signs fundamental in logic, epistemology, and metaphysics.
Peirce’s paper "On a New List of Categories" was presented to the academy on 14 May 1867. In his private Logic Notebook, on 23 March, Peirce wrote:
"I cannot explain the deep emotion with which I open this book again. Here I write but never after read what I have written for what I write is done in the process of forming a conception. Yet I cannot forget that here are the germs of the theory of the categories which is (if anything is) the gift I make to the world. That is my child. In it I shall live when oblivion has me—my body."
And thirty-eight years later, in a draft of a letter to Mario Calderoni, he could still write that
"on May 14, 1867, after three years of almost insanely concentrated thought, hardly interrupted even by sleep, I produced my one contribution to philosophy in the "New List of Categories." My three categories are nothing but Hegel's three grades of thinking. I know very well that there are other categories, those which Hegel calls by that name. But I never succeeded in satisfying myself with any list of them."
Readers of the present volume will bring to it numerous questions the editors cannot hope to anticipate. It seems safe to assume, however, that readers wishing to understand Peirce on his own terms will be more numerous than those who approach him with the same particular question or group of questions of their own. On that assumption, our primary aim in volume 1 has been to include in their chronological places the writings in which the reader can trace the steps by which Peirce arrived at his new list of categories, and at the first published forms of his general theory of signs and his sign theory of cognition; and in subsequent volumes the steps by which he moved through successive modifications of all three toward his last great undertaking, "A System of Logic, considered as Semeiotic." But we include every paper of comparable originality, whether directly relevant or not to this primary aim. No range of his work will be left unrepresented.
We turn now to a few of the less obvious early episodes in the search for the categories within the period of the present volume.
Charles Russell Lowell (eldest brother of the poet James Russell Lowell) and his wife, Anna Cabot Jackson Lowell, were neighbors of the Peirces. Their home was a center of hospitality. It was there that Peirce met Chauncey Wright, the ablest philosopher with whom he was personally acquainted in his early years. Shortly before he entered college, Mrs. Lowell had lent Peirce a copy of John Weiss translation of The Aesthetic Letters of Friedrich Schiller. As a result of alphabetic seating in their college classes, he and Horatio Paine ("noble-hearted, sterling-charactered," "almost the only real companion I have ever had") became intimate friends. Schiller's book interested them more than anything they were required to read in college, and they "spent every afternoon for long months upon it, picking the matter to pieces as well as we boys knew how to do." From Schiller they proceeded to Kant's Critic of the Pure Reason (as Peirce later rendered the title), and Peirce continued the study of the Critic until he almost "knew it by heart in both editions."
One of the assigned "themes" in their sophomore year was on a sentence from Ruskin's Modern Painters: "It has been said by Schiller in his letters on aesthetic culture that the sense of beauty never farthered the performance of a single duty." Peirce was well prepared to defend Schiller against Ruskin's misunderstanding. He gives an account of the three impulses distinguished by Schiller—the Formtrieb, Stofftrieb, and Spieltrieb. In response to a comment on his theme by their professor, Francis J. Child, Peirce added at the end: "I should say that these were the I impulse and faculty, and the IT impulse and faculty; and also the THOU impulse and faculty which (it seems to me) is what Schiller regards as that of beauty."
Readers familiar with Martin Buber's I and Thou will be struck by the prominence of I, IT, and THOU in the early stages of Peirce’s search for the categories. If Kant's categories come in triads, and if the Hegelian dialectic moves in triads of thesis, antithesis, and synthesis, and if Schiller finds only three fundamental drives or faculties, we may well be moved to try the hypothesis that Aristotle's ten categories and Kant's twelve are reducible to three. If, further, we expect the categories to manifest themselves in language as well as in thought, it may strike us that in the language we speak there is nothing more prominent than the three persons of the verb and the corresponding pronouns. (Some readers will recall at this point that Peirce later held that nouns are substitutes for pronouns, not, as their names assume, pronouns for nouns.)
If we then try finding our categories in, or deriving them from, the personal pronouns, our first trials are likely to take them in the order I, THOU, IT; and that is what Peirce does in his earliest surviving table, as well as in a theme comparing Michelangelo and Raphael, both written in 1857. In the table, he is already connecting his pronominal categories with Kant's triads; for that purpose he changes the order of the second and third categories in two of Kant's triads, and we wonder why he does not do so in the third as well.
By January 1859, if not earlier, he has settled on the order I, IT, THOU. In that month he begins a book on "The Natural History of Words," in which the first page of text reads:
THE PERSONS
I
I me
The
first person, the ego, the I, the Me, subject, self
Not-I non-ego
Subjective, my, mine
to me
IT
He him she her it they them, third person
Being, Thing, to ov thing in itself,
noumenon
be is are were was been
THOU
Thou, thee, ye, you; 0!
Second person,
thine, yours, thy,
your.
It is assumed throughout that semeiotic, the general theory of signs, including words and other symbols, is a classificatory science, like chemistry and biology; and we are starting with words, and, among words, with those associated with the three persons of the Verb, and with the names I, THOU, and IT for those persons. It is made emphatic that the logical or categorical order of these names is different from the traditional grammatical order of the persons, but the reason for the difference is not stated.
On 1 June 1859 Peirce constructs an octagonal table of subcategories of the IT, including all of Kant's categories with some puzzling alterations. Kant's first triad appears as Infinite Qualities of Quantity, his second as Influxual Dependencies of Quality, his third as Necessary Modes of Dependence, and his fourth as Perfect Degrees of Modality. These are followed by four other triads, the last of which brings us back to Kant's first.
In the spring of 1861 Peirce begins a book entitled, "I, IT, and THOU." "I here, for the first time," he writes, "begin a developement of these conceptions. . . . THOU is an IT in which there is another I. I looks in, It looks out, Thou looks through, out and in again." For the first time, it becomes emphatic and clear that THOU presupposes IT, and IT presupposes I. That is the reason for the difference between the categorical and the grammatical order.
In the next year, 1862, William James writes in one of his notebooks:
"The thou idea, as
Pierce calls it, dominates an entire realm of mental phenomena,
embracing poetry, all direct intuition of nature, scientific
instincts, relations of man to man, morality &c.
"All analysis must be into a triad;
me & it require the complement of thou."
In his oration on "The Place of Our Age in the History of Civilization," delivered at a reunion of the Cambridge High School Association on 12 November 1863 and published in the Cambridge Chronicle, Peirce says: "First there was the egotistical stage when man arbitrarily imagined perfection, now is the idistical stage when he observes it. Hereafter must be the more glorious tuistical stage when he shall be in communion with her."
In 1891 Peirce defines tuism for the Century Dictionary as "The doctrine that all thought is addressed to a second person, or to one's future self as to a second person." The Oxford English Dictionary later quotes this definition in its own entry. There and in its illeism entry, it is recorded that Coleridge had used the terms egotism, illeism, and tuism, but not in any systematic or technical way.
Though by 1867 Peirce has abandoned I, IT, and THOU as names for his categories, it is only because he has found better technical terms for what he has meant by those more colloquial ones.
The main substance of the present volume is in the two series of lectures on the logic of science—the Harvard University Lectures in the spring of 1865 and the Lowell Institute Lectures in the fall of 1866. Though a few extracts from both series have been published, the present volume contains for the first time as near an approach to a complete letterpress edition of the two as the surviving manuscripts make possible. It also enables us to attend both series with the benefit of prior acquaintance with several years of the young lecturer's life and work, and thereby prepares us for the second and subsequent volumes .
We are tempted to say on the one hand that in these two courses Peirce has for the most part unfolded his thoughts before us with such fullness that any editorial introduction would be superfluous, and on the other hand that an adequate introduction will be possible only after several years of detailed examination by Peirce scholars and by historians of logic.
If some readers find his metaphysics more interesting than his logic, we invite their attention to the last of the Lowell Lectures, on the advantages of "adopting our logic as our metaphysics." If we learn our logic from Peirce, we shall thereby be led, for example, not only to the sign theory of cognition but also to the sign (more exactly the symbol) theory of man, and to a metaphysics akin to trinitarian theology. Near the end, the lecturer is saying:
"Here, therefore, we have a divine trinity of the object, interpretant, and ground. . . . In many respects, this trinity agrees with the Christian trinity; indeed I am not aware that there are any points of disagreement. The interpretant is evidently the Divine Logos or word; and if our former guess that a Reference to an interpretant is Paternity be right, this would be also the Son of God. The ground, being that partaking of which is requisite to any communication with the Symbol, corresponds in its function to the Holy Spirit."
This becomes intelligible only in the light of biographical details more intimate than those we have so far cited.
Peirce was brought up a Unitarian. The family attended services at the College Chapel. Frederic Dan Huntington's appointment as Plummer Professor of Christian Morals and Preacher to the College began with Peirce’s freshman year and continued a year beyond his graduation It was under Huntington that Peirce in his freshman year studied Richard Whately's Lessons on Morals and Christian Evidences. Huntington was a Unitarian, but he became an Episcopalian early in 1860 and therefore resigned his professorship. (He later became the first Episcopal bishop of Central New York, with diocesan headquarters at Syracuse.)
Among the Harvard classmates of Peirce’s father was Charles Fay, who became an Episcopalian clergyman, married a daughter of John Henry Hopkins, the first Episcopal bishop of Vermont, and since 1848 had been rector of St. Luke's Episcopal Church at St. Albans, Vermont. The eldest daughter of the Fays, Harriet Melusina, usually called Zina, was a passionate feminist deeply concerned from adoescence about the role of women in society. In the summer of 1859 she arrived at an interpretation of the doctrine of the trinity according to which the Holy Spirit is the feminine element in the triune god-head: "a Divine Eternal Trinity of Father, Mother and Only Son—the 'Mother' being veiled throughout the Scriptures under the terms 'The Spirit,' 'Wisdom,' 'The Holy Ghost,' 'The Comforter,' and 'The Woman clothed with the sun and crowned with the stars and with the moon under her feet'."
After her mother's death in 1856, Zina had been in correspondence with Ralph Waldo Emerson, and it was on his advice that in the fall of 1859 she entered the Agassiz School for Young Ladies, in the Agassiz home just across Quincy Street from the Peirces. Perhaps it was there that Charles and Zina met, in the winter of 1860-61 if not earlier. He made his first formal call upon her in January 1861. Several of his metaphysical writings from 1861 onwards are marked "For Z. F.," and probably most if not all of them were written for her. In the summer of 1861 he made the first of several extended visits to Zina and her family in St. Albans. His "Views of Chemistry: sketched for Young Ladies," written for Zina and her younger sisters, were begun during that visit. When he defined his object in that year, it probably included marriage with her. By the spring of 1862 they were engaged. It seemed to his parents that for the first time he was taking religion seriously. In the evening of 24 July, in the chapel of the Vermont Episcopal Institute in Burlington, in the presence of Zina and several members of her family, Charles was confirmed by her grandfather, Bishop Hopkins. On 16 October Charles and Zina were married by her father at St. Luke's in St. Albans. (They had no children. After fourteen years together, she separated herself from him. He divorced her in 1883 and took a second wife. Zina did not remarry.)
Peirce’s conversion to Episcopalianism entailed of course a conversion from unitarianism to trinitarianism. Though not always an active communicant, he remained an Episcopalian and a trinitarian to the end of his life. And as late as 1907 we find a distant echo of Zina's feminist version of the trinity. In outlining a draft of what turned out to be his best account of pragmatism within the framework of his general theory of signs, he then wrote: "A Sign mediates between its Object and its Meaning. . . Object the father, sign the mother of meaning." That is, he might have added, of their son, the Interpretant.
Though Peirce’s categories are meant to be universally applicable, and he did so apply them, his most frequent single application of all three together is in the definition of a sign. In his many definifions, early and late, the nearest to a constant is that a sign is a first something so determined (limited, specialized) by a second something, called its object, as to determine a third something, called its interpretant, to determination by the same object. That is, sign action or semeiosis (as distinguished from dyadic mechanical action) involves an irreducibly triadic relation between (1) a sign, (2) its object, and (3) its interpretant.
His most frequent single occasion for defining a sign is that of a logician for whom logic is "the critic of arguments" and arguments are a kind of signs. After defining a sign, his most frequent next three moves, each a reapplication of his categories, are: (1) dividing signs into icons, indexes, and symbols; (2) dividing symbols into terms, propositions, and arguments; and (3) dividing arguments into retroductions, inductions, and deductions. He is then ready for the main business of logic, that of determining the relative validity or strength of each kind of arguments.
(In the present volume, he uses "representation" and "representamen" in approximately the senses in which he will later use "sign," and by "sign" he usually means what toward the end of the volume he begins calling "index." What in this volume he calls "likeness," "copy," "image," or "analogue," he will begin calling "icon" in 1885. "Abduction" and "retroduction" are his later and more technical terms for what he here calls "hypothesis" or "inference a' posteriori." For a short while he tries "subject" and "correspondent" for what, toward the end of the volume, he begins calling "interpretant.")
Logic is for Peirce a science, and its definition must therefore place it in relation to other sciences. That calls for a classification of the sciences. No logician—no philosopher—ever attached more importance, or devoted more attention, to classifications of the sciences than Peirce did. The most general and the most familiar classification was that which John Locke, in the last chapter of his Essay Concerning Human Understanding (1690), ascribed to the Greeks: [Greek] or natural science, [Greek] or moral science, and [Greek] or "the Doctrine of Signs, the most usual whereof being Words, it is aptly enough termed also [Greek], Logick." Peirce objects that, of the three kinds of signs, logic deals only with symbols, and with them only in relation to their objects, and only in respect of truth and falsity. Moreover, of the three kinds of symbols, it has little to say of terms and propositions except as they enter into arguments. So logic is at most but a third part of a third part—that is, a ninth part—of semeiotic. It might be defined as objective symbolistic.
By the mid-1880s, however, Peirce will have come to realize that logic cannot do business without icons and indexes and that it must take account of all three kinds of symbols both in themselves and in relation to their interpretants as well as in relation to their objects. In the 1890s he will distinguish a narrow sense in which logic is still concerned only with arguments and only in relation to their objects, and a broad sense in which it is coextensive with semeiotic in the sense of "the general theory of signs," leaving room for an indefinite number of more specialized semeiotic sciences. He is thus halfway back to Locke. By 1902, he will abandon the narrow sense altogether, or use Locke's term critic rather than logic as the name for it; and the semeiotic trivium will become the logical trivium of speculative grammar, critic, and speculative rhetoric or methodeutic; and by 1909 he is drafting "A System of Logic, considered as Semeiotic." It has taken him most of his productive lifetime to come all the way back to Locke. With this in mind, it should not surprise us that, over that lifetime, Peirce devoted more study than any other major logician has done to "the doctrine of signs."
Returning now to the classification of arguments, we remark that though the title of Peirce’s Harvard University Lectures of 1865 was simply "On the Logic of Science," that of his Lowell Institute Lectures of 1866 was "The Logic of Science; or, Induction and Hypothesis." The latter title would have been read at the time as if it had been written "The Logic of Science; or, Induction—and Hypothesis!" The common assumption was that the logic of mathematics was the logic of deduction, and the logic of science that of induction. Though it was obvious that the advancement of the empirical and experimental sciences depended on the forming and testing of hypotheses, hypothesis was not (and is not yet) understood as a distinct kind of inference or argument.
But Peirce’s three categories led him to expect to find three distinct kinds of arguments. (He later intimated that the chief single purpose of his work on the categories had been to have a guide to the classification of arguments.) The problem was to identify, distinguish, and name them. He began where Kant began in his major work, whose title Peirce proposed to translate "Critic of the Pure Reason"; namely, with the distinction between two kinds of "judgments": (1) analytic or explicative and (2) synthetic or ampliative. Peirce first adopted the second term of each pair. He then turned the distinction between explicative and ampliative judgments into the distinction between explicative and ampliative arguments or inferences. A possible way of coming out with three kinds instead of two was to divide one or the other into two. He would later distinguish two kinds of mathe-matical demonstration, corollarial and theorematic, but he had as yet no inkling of that. Even if he had already worked it out, the difference between them would not have seemed to him so radical as that between the two kinds of ampliative inference which he now readily found; the difference, that is, between induction more strictly speaking on the one hand, and on the other reasoning to a hypothesis that will both account for puzzling data already obtained and serve to predict results of experiments not yet tried or observations not yet made.
Peirce next connected explicative arguments with the first of the three Aristotelian figures of the syllogism, and more particularly with the mood Barbara. He then tried connecting hypothesis with the second figure, and particularly with the mood Baroco; and induction with the third figure, and particularly with the mood Bocardo. In the order of the validity or strength of the three kinds of arguments, from the weakest to the strongest, the connections thus became: (1) first category, hypothesis, second figure; (2) second category, induction, third figure; (3) third category, deduction, first figure.
But connecting the three kinds of inference with the three Aristotelian figures of the syllogism was open to two lines of attack. (1) What about the fourth figure? Having adopted as his "primary conceptions" those of rule, subsumption of case, and result, Peirce rejects the fourth figure and "all its moods not as being invalid but as being indirect, and unsyllogistic." (2) But since syllogisms in the second and third figures are reducible to syllogisms in the first, must we not concur with Kant in his early tract On the False Subtlety of the Four Syllogistic Figures? That question led Peirce to his first major discovery in logic; namely, that every such reduction takes the logical form of an argument in the figure from which the reduction is made. He thought enough of this discovery to have his essay on it privately printed in time for distribution at his Lowell Lectures in November 1866, under the title Memoranda Concerning the Aristotelean Syllogism; and he mailed copies to logicians at home and abroad. Augustus De Morgan in London received his copy on 29 December 1866. By the end of the period covered by the present volume, Peirce had thus joined the small international community of professional logicians.
MAX H. FISCH
The following five corrections to the first printing have been incorporated in the second printing; the original readings are given in brackets.
paper [papers]
of [or]
reasonableness [reasonbleness]
symbols [things]
blue [red]
Emendations for the last two, which represent Peirce’s own errors, have been added on pages 640 and 661.
The following nine corrections to the second printing have been incorporated in the third printing; the original readings are given in brackets.
familiar [familar]
forms manifested . . . symbols translated
[symbols translated . . . forms manifested]
denotation [information]
Chapter [Chaper]
rests is . . . conclusion,—this [rests—is . . . conclusion. This]
hypothesis [hyopthesis]
letzterer [letzerer]
A heavy dot has been inserted, centered under the short horizontal line at the top of that page
information, [information]
Emendations for 276.19–20, 277.11–12, and 484.11, which represent Peirce’s errors, have been added on pages 639 and 676; two emendations have been removed on page 668, for correction 435.27–29.
The following five corrections to the third printing have been incorporated in the fourth printing; the original readings are given in brackets.
and [is]
that what [that that what]
that which is not what a word denotes
[which what a word denotes is not]
mortals) [mortals]
écrits [ecrits]
Emendations for the first three errata, which represent Peirce’s errors, have been added on pages 658 and 671.
but three [but the]
three elements [both]
term [proposition]
terms [propositions]
other [first]
rule [case]
and [or]
everything [every thing]
But the extension of a general term [But the comprehension of a general term]
In short, the logical extension, [In short, the logical comprehension,]
a whole of extension. [a whole of comprehension.]
dark red colour has still less extension.
[dark red colour has still less comprehension.]
An Index term is one which has no adequate comprehension; [An Index term is one which has no adequate extension;]
The year in the running head on odd pages from 65 to 83 should read 1862 instead of 1861.
“Intellectual Symbolism” [Intellectual Symbolism]
only Images à posteriori recalled [only Images à priori recalled] Peirce’s error confirmed by 62.15–16
otherwise [other wise]
The interlineation b = 0 on line 19 should have been inserted just after the fifth word of line 20, to read:
either b is zero b = 0 or
for the plant [for plant]
MS 70 (920, 919, S66) [MS 70 (920, 919)]
MS 71 (1105, 921, 919, 741, 922) [MS 71 (1105, 921, 919, 741)]
MS 92 (1156a) 1864–1871 [MS 92 (1596) 1864–1869]
“I cannot explain the deep emotion with which I open this book again. . . . I cannot forget that here are the germs of the theory of the categories which is (if anything is) the gift I make to the world. That is my child. In it I shall live when oblivion has me—my body.”
Volume 2 (1867–1871) contains some of the major philosophical and logical writings of Peirce’s entire life. His epochal “New List of Categories” of 1867, his three “cognition” articles in the Journal of Speculative Philosophy of 1868–69, and his review of the works of Berkeley in the North American Review of 1871 are now recognized as constituting the modern founding of semiotics, the general theory of signs, while providing also a new fundamental platform for philosophy itself. If we add to these the 1867 review of Venn’s Logic of Chance, the 1867–68 critique of positivism, and the 1870 memoir, “Description of a Notation for the Logic of Relatives,” and read all eight in chronological order, we can trace the early stages of Peirce’s continued effort to redefine and clarify realism by disentangling it progressively from nominalism. His other papers in logic bring improvement to Boole’s calculus of logic; provide a natural classification of arguments that revisits the figures of syllogisms and tie them to induction, hypothesis, and analogy; work out a formal logic of mathematics; and make public Peirce’s research on logical comprehension and extension. Other essays and lectures testify to Peirce’s deep study of the works of British logicians.
When Peirce was appointed assistant in the United States Coast Survey in 1867, he began an ascent that carried him during the next decade to the select ranks of leadership in science in America and to renown in the international scientific community. The focus of Peirce’s scientific work during the period of the volume 2 was astronomy, and, by arrangement with the Coast Survey, his work was conducted principally at the Harvard Observatory. Peirce was an official observer of two total eclipses of the sun during these years, the first in Kentucky in 1869 and the second in Sicily in 1870. During the several months that Peirce spent in Europe in 1870–71, he became acquainted with many leading European astronomers. In 1871 he began his observations with Harvard’s Zöllner astrophotometer, which resulted in his only published monograph, Photometric Researches, parts of which are included in Volume 3.
“Whether men really have anything in common, so that the community is to be considered as an end in itself, . . . is the most fundamental practical question in regard to every public institution the constitution of which we have it in our power to influence.”
Volume 2 contains some of the major philosophical writings of Peirce’s entire life. His "New List of Categories" of 1867, his three "cognition" articles in the Journal of Speculative Philosophy of 1868-69, and his review of the works of Berkeley in the North American Review of 1871 are now recognized as constituting the modern founding of semiotics, the general theory of signs. If we add to these the 1867 review of Venn's Logic of Chance and the 1870 memoir on the "logic of relatives," and read all seven in chronological order, we can trace the early stages of Peirce’s progress from nominalism to realism. When Peirce was appointed assistant in the United States Coast Survey in 1867, he began an ascent that carried him during the next decade to the select ranks of leadership in science in America and to renown in the international scientific community.
The focus of Peirce’s scientific work during the period of the present volume was astronomy, and, by arrangement with the Coast Survey, his work was conducted principally at the Harvard Observatory. Peirce was an official observer of two total eclipses of the sun during these years, the first in Kentucky in 1869 and the second in Sicily in 1870. During the several months that Peirce spent in Europe in 1870-71, he became acquainted with many leading European astronomers. In 1871 he began his observations with Harvard's Zollner astrophotometer, which resulted in his only published monograph, Photometric Researches, parts of which are included in Volume 5.
| Preface | xi |
| Acknowledgments | xix |
| Introduction |
xxi
|
| The Decisive Year and Its Early Consequences Max H. Fisch | xxi |
| The Journal of Speculative Philosophy Papers C. V. Delaney | xxxvi |
| The 1870 Logic of Relatives Memoir Daniel D. Merrill | xlii |
| 1. [The Logic Notebook] | 1 |
|
[THE AMERICAN ACADEMY SERIES] |
|
| 2. On an Improvement in Boole's Calculus of Logic | 12 |
| 3. On the Natural Classification of Arguments | 23 |
| 4. On a New List of Categories | 49 |
| 5. Upon the Logic of Mathematics | 59 |
| 6. Upon Logical Comprehension and Extension | 70 |
| 7. Notes | 87 |
| 8. [Venn's The Logic of Chance] | 98 |
| 9. Chapter I. One, Two, and Three | 103 |
| 10. Specimen of a Dictionary of the Terms of Logic and allied Sciences: A to ABS | 105 |
| 11. [Critique of Positivism] | 122 |
|
[THE PEIRCE-HARRIS EXCHANGE ON HEGEL] |
|
| 12. Paul Janet and Hegel, by W. T. Harris | 132 |
| 13. Letter, Peirce to W. T. Harris (24 January 1868) | 143 |
| 14. Nominalism versus Realism | 144 |
| 15. Letter, Peirce to W. T. Harris (16 March 1868) | 154 |
| 16. What is Meant by "Determined" | 155 |
| 17. Letter, Peirce to W. T. Harris (9 April 1868) | 158 |
|
[THE JOURNAL OF SPECULATIVE PHILOSOPHY SERIES] |
|
| 18. Questions on Reality | 162 |
| 19. Potentia ex Impotentia | 187 |
| 20. Letter, Peirce to W. T. Harris (30 November 1868) | 192 |
| 21. Questions Concerning Certain Faculties Claimed for Man | 193 |
| 22. Some Consequences of Four Incapacities | 211 |
| 23. Grounds of Validity of the Laws of Logic | 242 |
| 24. Professor Porter's Human Intellect | 273 |
| 25. The Pairing of the Elements | 282 |
| 26. Roscoe's Spectrum Analysis | 285 |
| 27. [The Solar Eclipse of 7 August 1869] | 290 |
| 28. Preliminary Sketch of Logic | 294 |
| 29. [The Logic Notebook] | 298 |
| 30. The English Doctrine of Ideas | 302 |
|
[LECTURES ON BRITISH LOGICIANS] |
|
| 31. Lecture I. Early nominalism and realism | 310 |
| 32. Ockam. Lecture 3 | 317 |
| 33. Whewell | 337 |
|
[PRACTICAL LOGIC] |
|
| 34. Lessons in Practical Logic | 348 |
| 35. A Practical Treatise on Logic and Methodology | 350 |
| 36. Rules of Investigation | 351 |
| 37. Practical Logic | 353 |
| 38. Chapter 2 | 356 |
| 39. Description of a Notation for the Logic of Relatives | 359 |
| 40. A System of Logic | 430 |
| 41. [Henry James's The Secret of Swedenborg] | 433 |
| 42. Notes for Lectures on Logic to be given 1st term 1870-71 | 439 |
| 43. Bain's Logic | 441 |
| 44. Letter, Peirce to W. S. Jevons | 445 |
| 45. [Augustus De Morgan] | 448 |
| 46. Of the Copulas of Algebra | 451 |
| 47. [Charles Babbage] | 457 |
|
[THE BERKELEY REVIEW] |
|
| 48. [Fraser's The Works of George Berkeley] | 462 |
| 49. [Peirce’s Berkeley Review], by Chauncey Wright | 487 |
| 50. Mr. Peirce and the Realists | 490 |
|
APPENDIX |
|
| 51. Letter, J. E. Oliver to Peirce | 492 |
| Editorial Notes | 499 |
| Bibliography of Peirce’s References | 555 |
| Chronological List, 1867-1871 | 564 |
|
TEXTUAL APPARATUS |
|
| Essay on Editorial Method | 469 |
| Explanation of Symbols | 582 |
| Textual Notes | 584 |
| Emendations | 586 |
| Word Division | 629 |
| Index | 632 |
The most decisive year of Peirce’s professional life, and one of the most eventful, was 1867.
Superintendent Bache of the Coast Survey had been incapacitated by a stroke in the summer of 1864. He died on 17 February 1867. Benjamin Peirce became the third Superintendent on 26 February and continued in that position into 1874. He retained his professorship at Harvard and, except for short stays in Washington, he conducted the business of Superintendent from Cambridge. Julius E. Hilgard served as Assistant in Charge of the Survey's Washington office. On 1 July 1867 Charles was promoted from Aide to Assistant, the rank next under that of Superintendent. He continued in that rank for twenty-four and a half years, through 31 December 1891.
National and international awareness of the Survey was extended by two related episodes beginning in 1867. A treaty with Russia for the purchase of Alaska, negotiated by Secretary of State William Henry Seward, was approved by the Senate on 9 April, but the House delayed action on the appropriation necessary to complete the transaction. Superintendent Peirce was asked to have a reconnaissance made of the coast of Alaska, and a compilation of the most reliable information obtainable concerning its natural resources. A party led by Assistant George Davidson sailed from San Francisco on 21 July 1867 and returned 18 November 1867. Davidson's report of 30 November was received by Superintendent Peirce in January, reached President Johnson early in February, and was a principal document in his message of 17 February to the House of Representatives, recommending the appropriation. The bill was finally enacted and signed by the President in July.
Charles's younger brother, Benjamin Mills Peirce, returned in the summer of 1867 from two years at the School of Mines in Paris. Seward wished to explore the possibility of purchasing Iceland and Greenland from Denmark. His expansionist supporter Robert J. Walker consulted Superintendent Peirce, who had his son Ben compile A Report on the Resources of Iceland and Greenland which he submitted on 14 December 1867, and which his father submitted to Seward on the 16th. With a foreword by Walker, it was published in book form next year by the Department of State. But congressional interest in acquiring the islands was insufficient and no action was taken. 1
Joseph Winlock had become the third Director of the Harvard College Observatory in 1866, and working relations between the Survey and the Observatory became closer than they had previously been. (Winlock had been associated with the American Ephemeris and Nautical Almanac from its beginning in 1852, and for the last several years had been its Superintendent, residing in Cambridge. Benjamin Peirce had been its Consulting Astronomer from the beginning. Charles had done some work for it in recent years. Assistant William Ferrel and he had observed the annular eclipse of the sun at St. Joseph, Missouri, 19 October 1865, and both had submitted written reports to Winlock which are still preserved.) By arrangement with Winlock, Charles began in 1867 to make observations at the Observatory that were reported in subsequent volumes of its Annals. In 1869 he was appointed an Assistant in the Observatory, where, as in the Survey, the rank of Assistant was next to that of Director.
In 1867 the Observatory received its first spectroscope. Among the most immediately interesting of the observations it made possible were those of the auroral light. In volume 8 of the Annals it was reported that "On April 15, 1869, the positions of seven bright lines were measured in the spectrum of the remarkable aurora seen that evening; the observer being Mr. C. S. Peirce."
By that time, Peirce had begun reviewing scientific, mathematical and philosophical books for the Nation. His second review was of Roscoe's Spectrum Analysis, on 22 July 1869, and it was both as chemist and as astronomer that he reviewed it. With Winlock's permission, he reported that
"In addition to the green line usually seen in the aurora, six others were discovered and measured at the Harvard College Observatory during the brilliant display of last spring, and four of these lines were seen again on another occasion. On the 29th of June last, a single narrow band of auroral light extended from east to west, clear over the heavens, at Cambridge, moving from north to south. This was found to have a continuous spectrum; while the fainter auroral light in the north showed the usual green line."2
Peirce was a contributor to the Atlantic Almanac for several years, beginning with the volume for 1868. In that for 1870 he had, among other things, an article on "The Spectroscope," the last paragraph of which was devoted to the spectrum of the aurora borealis and the newly discovered lines.
As an Assistant both in the Survey and in the Observatory, Peirce was an observer of two total eclipses of the sun, at Bardstown, Kentucky, 7 August 1869, and near Catania, Sicily, 22 December 1870. And as late as 1894 he would write: "Of all the phenomena of nature, a total solar eclipse is incomparably the most sublime. The greatest ocean storm is as nothing to it; and as for an annular eclipse, however close it may come to totality, it approaches a complete eclipse not half so near as a hurdy-gurdy a cathedral organ."
In 1871 the Observatory acquired a Zšllner astrophotometer and Winlock made Peirce responsible for planning its use. More of that in our next volume. And in 1871 Peirce’s father obtained authorization from Congress for a transcontinental geodetic survey along the 39th parallel, to connect the Atlantic and Pacific coastal surveys. This led to Charles's becoming a professional geodesist and metrologist; but that too is matter for the third and later volumes. Back now to 1867.
One of the most famous cases that ever came to trial was the Sylvia Ann Howland will case, and the most famous of the many famous things about it was the testimony of the Peirces, 5 and 6 June 1867. The questions at issue were (1) whether Miss Howland's signatures to the two copies of the "second page" codicil of an earlier will were genuine, or were forged by tracing her signature to the will itself, and (2) whether, supposing them genuine, the codicil invalidated a later will much less favorable to her niece, Hetty H. Robinson. The Peirces addressed themselves to the first of these questions. Under his father's direction, Charles examined photographic enlargements of forty-two genuine signatures for coincidences of position in their thirty downstrokes. In 25,830 different comparisons of downstrokes, he found 5,325 coincidences, so that the relative frequency of coincidence was about a fifth. Applying the theory of probabilities, his father calculated that a coincidence of genuine signatures as complete as that between the signatures to the codicil, or between either of them and that to the will in question, would occur only once in five-to-the-thirtieth-power times. The judge was not prepared to base his decision on the theory of probabilities, but he decided against Miss Robinson on the second issue.3 In the Nation for 19 September 1867, under the title "Mathematics in Court," there appeared a letter to the editor criticizing Benjamin Peirce’s testimony, and a long reply signed "Ed. Nation" but written by Chauncey Wright, concluding that "The value of the present testimony depends wholly on the judgment of his son in estimating coincidences, and does not depend on the judgment of either father or son as mathematical experts." In a long article on "The Howland Will Case" in the American Law Review for July 1870 it was said that: "Hereafter, the curious stories of Poe will be thought the paltriest imitations."
Through 1867 (and on beyond) Peirce made frequent additions to his library in the history of logic. In March and April he acquired early editions of Duns Scotus. On 1 January 1868 he compiled a "Catalogue of Books on Mediaeval Logic which are available in Cambndge"—more of them in his own library than at Harvard's or anywhere else.
Charles W. Eliot became President of the University on 19 May 1869. Two days later he wrote to George Brush of Yale: "what to build on top of the American college. . . . This is what we have all got to think about." His first thought was to try turning the University Lectures into sequences running through the academic year, with optional comprehensive examinations on each sequence at the end of the year. He arranged two such sequences for 1869-70; one in philosophy, the other in modern literature. For philosophy he enlisted Francis Bowen, John Fiske, Peirce, F. H. Hedge, J. Elliott Cabot, Emerson, and G. P. Fisher, in that order. Peirce’s fifteen lectures, from 14 December to 15 January, were on the history of logic in Great Britain from Duns Scotus to Mill. William James attended at least his seventh, on nominalism from Ockham to Mill, and wrote next day to his friend Henry P. Bowditch that "It was delivered without notes, and was admirable in matter, manner and clearness of statement.... I never saw a man go into things so intensely and thoroughly." The Graduate School was not established until 1890, with James Mills ("Jem") Peirce, Charles's older brother, as Dean; but the experiment of 1869-70 was later called "The Germ of the Graduate School."4
Back again to 1867. On 30 January Peirce was elected a Resident Fellow of the American Academy of Arts and Sciences. He presented three papers to the Academy at its meetings of 12 March, 9 April, and 14 May, and two further papers at those of 10 September (read by title only) and 13 November. The volume of the Academy's Proceedings which included all five of these papers did not appear until the following year, but by November 1867 Peirce had obtained collective offprints of the first three under the title "Three Papers on Logic" and had begun distributing them. He began receiving responses early in December.5
The first philosophical journal in the United States—indeed the first in English anywhere—was the quarterly Journal of Speculative Philosophy, published in St. Louis and edited by William Torrey Harris. It began with the issue for January 1867. Peirce subscribed at first anonymously through a bookseller. But as soon as the collective offprints of "Three Papers on Logic" were ready, he sent Harris a copy. Harris responded with a letter dated 10 December 1867. He was especially interested in Peirce’s third paper, "On a New List of Categories." (Peirce himself as late as 1905 called it "my one contribution to philosophy.") In response to Harris, Peirce wrote a long letter on Hegel which he did not mail and a short letter dated 1 January 1868 which he did mail. Thus began the correspondence that led to five contributions by Peirce to the second volume of the Journal: two anonymous exchanges with the editor, and three articles under his own name in response to the editor's challenge to show how on his nominalistic principles "the validity of the laws of logic can be other than inexplicable." (These five contributions are examined in detail by C. F. Delaney in part II of the present introduction.)
In giving the title "Nominalism versus Realism" to the first exchange, Harris obviously meant to call Peirce a nominalist and Hegel and himself (and other followers of Hegel) realists. Peirce did not disclaim the nominalism. But was he a professing nominalist, and did Harris know that he was? And, if so, how did he know it?
That question takes us back again to 1867. At the end of the first of his "Three Papers on Logic" Peirce advocated a theory of probability for a fuller account of which he referred to his review of Venn's Logic of Chance. In that review he called it the nominalistic theory, as opposed to the realistic and conceptualistic theories. But Venn, though he used the latter two terms, nowhere used the terms nominalism, nominalistic, or nominalist. (The terms he did use are "material" and "Phenomenalist.") Evidently, therefore, Peirce wished to make his own commitment to nominalism unmistakable.
When did Peirce become a professing nominalist? Probably in 1851, about the time of his twelfth birthday, when he read Whately's Elements of Logic.
Where is the evidence in volume 1 of the present edition that he was a professing nominalist during the period of that volume? In what he says about the falsity of scholastic realism on pages 307 and 312 and in other relevant passages on pages 287, 306, and 360.6 And that he was still a professing nominalist when he began drafting his Journal of Speculative Philosophy articles, commonly called his cognition series," appears from what he says on pages 175, 180 and 181 of the present volume: "Thus, we obtain a theory of reality which, while it is nominalistic, inasmuch as it bases universals upon signs, is yet quite opposed to that individualism which is often supposed to be coextensive with nominalism." "Now the nominalistic element of my theory is certainly an admission that nothing out of cognition and signification generally, has any generality...."" If this seems a monstrous doctrine, remember that my nominalism saves me from all absurdity."
But in the published form of the second article, in the paragraph on page 239 of the present volume, Peirce unobtrusively takes his first step from nominalism toward realism. 7 "But it follows that since no cognition of ours is absolutely determinate, generals must have a real existence. Now this scholastic realism is usually set down as a belief in metaphysical fictions"—as Peirce himself had set it down on pages 287, 307, 311 and 312 of our first volume. It is the realism of Scotus to which he now commits himself. He takes a second and much more emphatic step in his Berkeley review three years later. He says there (on page 467 below) that Scotus "was separated from nominalism only by the division of a hair." What was the hair that Scotus split, we might ask, and how did he split it? Instead, going back once more to 1867 and taking the "New List of Categories" together with the three articles of the cognition series (1868-1869) and the Berkeley review (1871), let us ask what hairs Peirce split and how he split them.
As we remarked on page xxvi of the introduction to volume 1, Peirce’s "is the first list of categories that opens the way to making the general theory of signs fundamental in logic, epistemology, and metaphysics." We may add here that the "New List" together with the cognition series and the Berkeley review—five papers in all, and all five contained in the present volume—are now recognized as constituting the modern founding of semeiotic, the general theory of signs, for all the purposes of such a theory.8
Now for the hairsplitting. The Berkeley review is much more emphatic than the cognition series on the distinction between the forward and the backward reference of the term "reality" and the identification of nominalism with the backward and of realism with the forward reference. Which amounts to a semeiotic resolution of the controversy. Of the three central categories, quality is monadic, relation dyadic, and representation irreducibly triadic. The sign represents an object to or for an interpretant. But we may focus on the sign-object or on the sign-interpretant. If the question is whether there are real universals, the nominalists turn backward to the sign-object and do not find them; the realists turn forward to the sign-interpretant and find them (pp. 467 ff. below). That is primarily because the backward reference to the object is more individualistic, and the forward reference to the interpretant is more social. So realism goes with what has been called the social theory of logic, or "logical socialism."9 If we were selecting key sentences from the Peirce texts in the present volume, they might well include these two: (1) "Thus, the very origin of the conception of reality shows that this conception essentially involves the notion of a COMMUNITY, without definite limits, and capable of an indefinite increase of knowledge" (p. 239). (2) "Whether men really have anything in common, so that the community is to be considered as an end in itself, and if so, what the relative value of the two factors is, is the most fundamental practical question in regard to every public institution the constitution of which we have it in our power to influence" (p. 487).
The forward reference and the community emphasis owed something to Charles's wife Zina. By 1865 they were settled in a home of their own at 2 Arrow Street in Cambridge, and it remained their home throughout the period of the present volume. Arrow Street shot eastward from Bow Street into what was then Main Street but is now Massachusetts Avenue. The Arrow Street years were a period of experimentation and productivity for Zina as well as for Charles. Her major concerns were three: (1) reducing the burden of housekeeping drudgery for married women, (2) creating institutions to give women a voice in public affairs without their having to compete with men, and (3) higher education for women. For the first she advocated "Co-operative Housekeeping" in a series of five articles in the Atlantic Monthly from November 1868 through March 1869, when Charles's Journal of Speculative Philosophy series was appearing. Her articles reappeared in book form in Edinburgh and London in 1870. She also took a leading part in the organization of the short-lived Cambridge Co-operative Housekeeping Society, which rented the old Meacham House on Bow Street for its meetings as well as for its laundry, store, and kitchen. For her second concern, she was active in the movement for a "Woman's Parliament" and was elected president of its first convention in New York City, on 21 October 1860. That movement was still active under the name of "The Women's Congress" at least as late as 1877. For her third concern, she was one of the organizers of the Woman's Education Association of Boston, and her work in it was part of the pre-history of Radcliffe College.
Though Charles never became active in politics, he was an advocate of proportional representation. Zina made notes of his conversations with her about it, and published his views in two of her later books.
Though Zina was not a scientist, she did become a member of the international scientific community by serving, like Charles, as an observer near Catania in Sicily of the total eclipse of the sun on 22 December 1870 and by the inclusion of her excellent account of it in the annual report of the Coast Survey for that year.
Zina's younger sister Amy Fay was a gifted pianist who, after the best training that could be had in New England, studied in Germany from 1869 to 1875 under several of its best teachers, including Tausig, Kullak, and Deppe in Berlin and Liszt in Weimar. By visiting her in Germany and by reading her long and frequent letters home, Zina and Charles became vicarious members of the international community of musicians. Zina published selections from the letters in the Atlantic Monthly for April and October 1874, and later a more comprehensive collection in book form, in a single chronological order, under the title Music-Study in Germany. It went through more than twenty editions, was translated into French and German, and is still in print. The first twelve chapters come within the period of the present volume. One of them contains a vivid account of the five days that Amy and Charles spent in Dresden in August 1870.
Within the period of the present volume Peirce became acquainted with modern German experimental psychology, as represented by Weber, Fechner, Wundt, and Helmholtz. By 1869 he was already contemplating experiments of the kind he carried out with Jastrow in 1884, which made him the first modern experimental psychologist on the American continent. He sent Wundt copies of his Journal of Speculative Philosophy papers and asked permission to translate Wundt's Vorlesungen jiber die Menschen- und Thierseele,to which he refers in appreciative terms on page 307 below. Wundt's reply thanking him for the papers and granting the permission was dated at Heidelberg 2 May 1869. No translation by Peirce was published, and no drafts have been found. A translation of the much revised edition of 1892 was published by J. E. Creighton and E. B. Titchener in 1894 and reviewed by Peirce in the Nation. When Helmholtz visited New York City in 1893, Peirce had a visit with him, and his long obituary of Helmholtz in 1894 was reprinted in Pollak's 1915 anthology of the Nation's first fifty years.
Back now to logic. In his Harvard University Lectures on the logic of science in the spring of 1865, a few months after the death of George Boole, Peirce had said that Boole's 1854 Investigation of the Laws of Thought "is destined to mark a great epoch in logic; for it contains a conception which in point of fruitfulness will rival that of Aristotle's Organon (W1:224). In the first of his fifteen Harvard University Lectures of 1869-70 on "British Logicians," before turning to medieval nominalism and realism, Peirce said, according to the notes of one of his students, that there was enough in Boole to "take the whole time" of the course. By 1877 the British mathematician and philosopher W. K. Clifford was ready to say that "Charles Peirce. . . is the greatest living logician, and the second man since Aristotle who has added to the subject something material, the other man being George Boole, author of The Laws of Thought." 10
What was the "something material" that Peirce had added? That takes us back once more to 1867, for it certainly included "On an Improvement in Boole's Calculus of Logic." What else? At the very least, and above everything else, the most difficult and, at least for logicians and for historians of logic, the most important paper in the present volume: "Description of a Notation for the Logic of Relatives, resulting from an Amplification of the Conceptions of Boole's Calculus of Logic" (DNLR).11 But is it not the case that, though the logic of relations can be traced back at least to Aristotle, De Morgan was the first logician to invent a notation for it? And was not that in 1860, a decade before Peirce’s memoir? Yes, but as soon as Peirce’s memoir began to circulate, there was room for the question whether De Morgan's notation might be a dead end. In his obituary of De Morgan, Peirce said (p. 450 below) "it may at least be confidently predicted that the logic of relatives, which he was the first to investigate extensively, will eventually be recognized as a part of logic." He did not predict, however, that it would be in De Morgan's notation that it would achieve that recognition. But was not the Boole-Peirce-Schršder line in logic superseded by the Frege-Peano-Russell-Whitehead line? No; it was only eclipsed.
Even more intimately than with Boole and De Morgan, Peirce associated his DNLR with his father's Linear Associative Algebra. The two appeared at almost the same time, midway between two total eclipses of the sun, but the connections between them did not become fully apparent until, after his father's death in 1880, Peirce prepared a second edition of the LAA, with an addendum by his father and two addenda by himself, and with well over a hundred footnotes to the original text, in over sixty of which he supplied translations from the LAA formulas into DNLR formulas.
Peirce’s father had been one of the founding members of the National Academy of Sciences in 1863. Beginning in 1867, he presented instalments of the LAA at meetings of the Academy.12 Charles's focus on the logic of relations went back to his earliest work on his categories. A logician who had only three central categories—Quality, Relation, and Representation—was bound to return again and again to the logic of relations. Recall, for example, his remarks about equiparant and disquiparant relations in volume 1, and note what he says about mathematical syllogisms on 42 f. below. But his earliest published mention of De Morgan's paper of 1860 was written late in 1868 (p. 245n2), and he may not have seen that paper more than a few weeks earlier. So the actual composing of the DNLR may have begun in 1869.
Then, on 7 August 1869, came the first of the two eclipses. It was observed by several teams at several points along the line of totality. Peirce and Shaler were stationed at Bardstown, Kentucky. Their report, one of the most vivid as well as detailed, was submitted by Peirce to Winlock, included in Winlock's report to Superintendent Peirce, and published by him in the Survey's Annual Report. It reappears on pages 290-93 below. A quarter of a century later, in an unpublished paper entitled "Argon, Helium, and Helium's Partner," Peirce gave an equally vivid retrospective account (Robin MS 1036).
"I remember, as if it were yesterday, the first time I saw helium. It was in 1869. Astronomical spectroscopy was then in its earliest infancy. . . . It was impossible in those early days, for the same observer to point his telescope and to use the spectroscope; so I had brought along with me the Kentuckian geologist Shaler, a man of nerve and proved in war, to bring successively the different protuberances of the sun upon the slit of my spectroscope, while I examined the spectrum and recognized what I could."
The observations of the sun's corona and protuberances by the Peirce-Shaler and other teams prompted new theories as to the composition of the sun, but there was some skepticism about these theories among European astronomers. The earliest opportunity for a test of them would be the eclipse of 22 December 1870, whose path of totality was to pass through the Mediterranean. It was desirable that as many as possible of the American observers of the 1869 eclipse should be observers of the 1870 one also, and Peirce’s father began making plans to bring that about. One of these plans was to have Charles follow the path of totality from east to west several months in advance, inspecting possible sites for observation parties, reporting to his father and to Winlock, and making tentative preliminary arrangements. But if Charles was to be in Europe for six or more months and his father for two or more, those interruptions might be detrimental to the major works they had in progress. It would be advantageous to finish them before leaving, and even more advantageous to take published copies with them, each of the other's work as well as his own, and get them that much sooner into the hands of the mathematicians and logicians they hoped to be meeting.
At the 616th meeting of the American Academy, on 26 January 1870, as reported by Chauncey Wright, its Recording Secretary, "The President . . . communicated by title . . . a paper 'On the Extension of Boole's System to the Logic of Relations by C. S. Peirce’." Late in the spring, Peirce supplied final copy; it was set in type and he was given fifty copies in paperback quarto book form, dated Cambridge 1870, "Extracted from the Memoirs of the American Academy, Vol. IX," though that volume did not appear until three years later.
Also late in the spring, since the National Academy, only seven years old, had as yet no funds for printing the papers or books its members presented, Julius E. Hilgard, a fellow member of the Academy, took Superintendent Peirce’s manuscript, had it copied in a more ornate and legible hand, and then had fifty copies lithographed from it.
When Charles sailed from New York on 18 June 1870, he took with him copies of the lithographed book and the printed memoir. In London on 11 July he delivered one of each, with a covering letter from his father, to De Morgan's residence. On a later day he had a visit with De Morgan, who, unfortunately, was already in the final decline that ended in his death in the following March, eleven days after Charles's return to Cambridge.
Charles presented another copy of the DNLR to W. S. Jevons, from whom he received a letter about it farther along on his eastward journey, to which he replied from Pest on 25 August (pp. 445-47 below).
Directly or indirectly, Robert Harley too received a copy. At the Liverpool meeting of the British Association for the Advancement of Science in September, Harley first presented "Observations on Boole's 'Laws of Thought' by the late R. Leslie Ellis," and then a paper by himself "On Boole's 'Laws of Thought'" (continuing one he had presented four years earlier), in which, after reviewing recent works by Jevons, Tait, and Brodie, he said: "But the most remarkable amplification of Boole's conceptions which the author has hitherto met with is contained in a recent paper by Mr. C. S. Peirce, on the 'Logic of Relatives'." He proceeds to quote the passage on "the three grand classes" of logical terms that appears on pages 364-65 below, and then the sentence that appears on page 359: "Boole's logical algebra has such singular beauty, so far as it goes, that it is interesting to inquire whether it cannot be extended over the whole realm of formal logic, instead of being restricted to that simplest and least useful part of the subject, the logic of absolute terms, which, when he wrote, was the only formal logic known." "The object of Mr. Peirce’s paper," he went on, "is to show that this extension is possible," and he gave some account of the notation and processes employed.
So Clifford was not alone in thinking that Peirce was "the second man since Aristotle." He was present at the meeting and spoke "On an Unexplained Contradiction in Geometry." He and Peirce may have met in London in July, and he too may then have received a copy of DNLR. If not, they almost certainly met as eclipse observers near Catania in December. In any case, they became well acquainted not later than 1875.
Two brief examples now of Benjamin Peirce’s distribution of copies of LAA. In Berlin, on his way to Sicily in November, he gave two copies to our ambassador, his old friend and former colleague, the historian George Bancroft; one for himself and one to present to the Berlin Academy, of which he was a member. And in January, after the eclipse, he addressed the London Mathematical Society on the methods he had used in his LAA, and presented a copy to the Society. Clifford was present and proposed the name "quadrates" for the class of the algebras that includes quaternions, and the Peirces adopted the proposal.
From London in the last week of July 1870, shortly after the Vatican Council had declared the conditions of papal infallibility, and just as the Franco-Prussian War began, Charles journeyed eastward by way of Rotterdam, Berlin, Dresden, Prague, Vienna, Pest, the Danube, and the Black Sea, to Constantinople. Then he began moving westward along the path of totality in search of eligible sites. (He recommended sites in Sicily and southern Spain, and became himself a member of one of the Sicilian teams.) In Berlin he visited Amy Fay, and she accompanied him to Dresden, chiefly for visits to the great art museum there. In Vienna, the director of the Observatory was hospitable and helpful. From Pest, he wrote the letter to Jevons. In Constantinople he enjoyed the guidance of Edward H. Palmer, "the most charming man" he had so far known, and of Palmer's friend Charles Drake; and he began the study of Arabic. In Thessaly he found the English consul most helpful, and the impressions he formed there he later worked up into "A Tale of Thessaly" of which he gave several readings. From Chambery in Savoy, after his visit to Spain, he wrote to his mother on 16 November 1870, five weeks before the eclipse, that he had heard eighteen distinct languages spoken, seventeen of them (including Basque) in places where they were the languages of everyday speech.
On the whole, the American observations and inferences of the preceding year were vindicated. This was Peirce’s first experience of large-scale international scientific cooperation. He had already committed himself to the social theory of logic, but this experience and those of his four later European sojourns confirmed him in that commitment.
Julius E. Hilgard, the Assistant in Charge of the Survey's Washington Office, which included the Office of Weights and Measures until the creation of the National Bureau of Standards in 1901, was to spend several months in Europe in mid-1872. Among other duties, he was to represent the United States at a Paris conference looking toward the international bureau of weights and measures which was finally established there in 1875. Peirce was to substitute for Hilgard in his absence, and that called for several weeks of previous training under Hilgard's supervision. He spent most of December 1871 and part of January 1872 at the new quarters of the Survey in the elegant Richards Building on Capitol Hill, where the Longworth House Office Building now stands. Hilgard gave good reports of his progress.
Hilgard's European sojourn would of course enhance his qualifications for succeeding Peirce’s father as Superintendent of the Survey. Peirce’s training and experience would qualify him to succeed Hilgard in case of Hilgard's death or resignation or promotion to Superintendent. It would even qualify him, under conceivable future circumstances, to be considered for the superintendency.
The Philosophical Society of Washington (in whose name, as in that of the American Philosophical Society in Philadelphia, "philosophical" meant scientific) had held its first meeting on 13 March 1871. At its 17th meeting, on 16 December 1871, Charles presented the first of the six wide-ranging papers he presented to that Society. It was "On the Appearance of Encke's Comet as Seen at Harvard College Observatory.''
Charles's father was to address the Cambridge Scientific Club on 28 December 1871 on the application of mathematics to certain questions in political economy, such as price and amount of sale, and the conditions of a maximum. Charles undertook to prepare diagrams for his father to exhibit at that meeting, and these were mailed to Cambridge on or about the 19th.
Simon Newcomb, then at the Naval Observatory, called on Charles on the 17th and they conversed about these matters. (Fifteen years later Newcomb published a book entitled Principles of Political Economy on which Charles commented adversely.) In the evening after the visit Charles wrote Newcomb a letter explaining what he had meant by saying that the law of supply and demand holds only for unlimited competition, and concluded: "P.S. This is all in Cournot." (On the strength of this letter, Baumol and Goldfeld recently included Peirce among their Precursors in Mathematical Economics.) In the same evening, Charles wrote to his wife Zina, who had remained in Cambridge, that he had been spending his evenings on political economy, and gave her some account of the questions he had been pursuing. On the 19th, he wrote a letter to his father, beginning: "There is one point on which I get a different result from Cournot, and it makes me suspect the truth of the proposition that the seller puts his price so as to make his profits a maximum." 13
Charles's own principal contribution to economics, his 1877 "Note on the Theory of the Economy of Research," will be included in our next volume, but these three letters are evidence that he brought to that particular topic a more general competence in economic theory.
But what, finally, of the Metaphysical Club at Cambridge, in which pragmatism was born? According to the best evidence we now have, it was founded not later than January 1872, after Peirce’s return from Washington. The introduction to volume 3 will resume the story at that point. But from a consecutive and careful reading of the present volume it will already be evident that pragmatism was the natural and logical next step.
II
The Journal of Speculative Philosophy papers of 1868-69 fall into two quite distinct groups. The first set is composed of a series of interchanges between C. S. Peirce and W. T. Harris (the editor of the journal) on issues of logic and speculative metaphysics that emerge from the philosophy of Hegel. The second set of papers, quite different in tone, consists of Peirce’s classic papers on cognition and reality, and the relatively neglected concluding paper of the series on the grounds of validity of the laws of logic.
1.
The Peirce-Harris exchange on Hegelian logic and metaphysics was occasioned by Harris's review article entitled "Paul Janet and Hegel" which appeared in his own journal. This was a long critical review of Janet's Etudes sur la dialectique dans Platon et dans Hegel, published in Paris in 1860. The exchange itself consists of letters from Peirce to Harris, two of which the latter transformed into dialectically structured discussion articles for his journal.
After some extensive preliminaries about the spread of Hegelianism, the original Harris article (like Janet's book that it reviews) focuses on Hegel's logic and follows Janet's tripartite division into "The Beginning," "The Becoming," and "The Dialectic." In the section labeled "The Becoming" Harris takes issue with Janet's account of the relation of Being and Nothing and the consequent genesis of Becoming. This is the problem that interested Peirce, and in his initial letter (24 January 1868) he takes issue with Harris's own account of the matter. These comments, together with his own replies, Harris published under the title "Nominalism versus Realism."
Peirce’s criticisms take the form of five inquiries seeking clarification. Initially he raises some general questions about Harris's doctrine of abstraction; then he raises three sets of questions about what he understands to be Harris's three arguments for the identity of Being and Nothing; finally he suggests, contrary to what he takes to be Harris's view, that the ordinary logical strictures against contradiction should at least have the presumption in their favor. Harris's response to these criticisms is most interesting, particularly in the light of Peirce’s mature philosophy. He maintains that the tone of Peirce’s initial set of questions about abstraction suggests that Peirce is committed both to nominalism and to a doctrine of immediacy, and that Peirce’s consequent specific criticisms of his three arguments bear his suspicion out. Peirce’s specific objections draw on formal logic's strictures against contradiction which, Harris maintains, are only adequate to the immediate world of independent things. But, Harris concludes, if one is to be a true speculative philosopher one must transcend this nominalism and become a realist.
Needless to say, Peirce thought that this response totally missed the point. In his follow-up letter, he makes the suggestion that a great deal of the misunderstanding between them may flow from certain unclarities with regard to the term "determined" as it functions in the discussion of Being and its determinations. He distinguishes several senses of "determine," "abstract," and "contradiction" in an attempt to move the discussion forward. Again, Harris published these comments together with his own terse responses, this time under the title "What Is Meant by 'Determined'."
One of the most obvious characteristics of this interchange on Hegel's logic is the marked difference between Harris's sympathy with the dialectical logic of the Hegelian tradition and Peirce’s employment of ordinary formal logic. Harris's request that Peirce do something for his journal on the rationale of the objective validity of the laws of logic is a happy outgrowth of this basic difference between the two. In his letter of 9 April 1868 Peirce responds that he has already devoted considerable time to this subject and could not adequately treat the issue in less than three articles. He enclosed the first of his three classic 1868 papers on cognition.
2.
Peirce’s 1868 papers on cognition, reality, and logical validity bring up the questions that were to be central throughout his whole philosophical career. In these he articulates his many-faceted attack on the spirit of Cartesianism, a spirit which he sees dominating most of modern philosophy. The Cartesian concern with skeptical doubt, individual justification, immediate knowledge and certainty (which traits he also saw in the empiricists), he seeks to replace by a view of knowledge that was through and through mediate, that construed knowledge as both an historical and communal human activity. From this perspective on knowledge, he proceeds to work through a concept of intersubjectivity to a full-blown account of objectivity, truth, reality, and the basis of the validity of the laws of logic.
The first piece included here is MS 148, consisting of three separately titled sections listed as "Questions on Reality" in the Contents. The third section, entitled "Questions concerning Reality," is an early version of the first published paper in the series, "Questions Concerning Certain Faculties Claimed for Man," but it is most interesting in its own right. In the first place, it is an heroic attempt to handle in a unified way all the issues that would eventually be divided among the three published papers in the 1868-69 series. The unity of the overall project is brought out forcefully in the introductory paragraph of the piece. Here Peirce makes the point that the logician's initial concern is with the forms of language but that he must inevitably push on from here to consider what we think, that is, the manner of reality itself; and, as a precondition for this inquiry, must get clear about the proper method for ascertaining how we think. His order of treatment, then, is, first, to give an account of cognition; secondly, to give an account of truth and reality; and, finally, to deal with some issues of formal logic. It is instructive to note that all three of these topics are treated under the general heading "Questions concerning Reality," indicating a metaphysical thrust that might be overlooked given the final titles: "Questions Concerning Certain Faculties Claimed for Man," "Some Consequences of Four Incapacities," and "Grounds of Validity of the Laws of Logic: Further Consequences of Four Incapacities."14 It is further instructive to glance over the twelve questions Peirce poses for himself in the outline given in the first section of MS 148 and observe how they reappear in the three published pieces.
The first six questions have to do with an
account of thinking and with the methodology appropriate in generating
such an account; and it is these six questions that make up the
substance of the first published paper in the series, "Questions
Concerning Certain Faculties Claimed for Man." The central issue is
whether we have any immediate knowledge at all (of ourselves, our mental
states, or the external world) and Peirce answers in the negative. In
the process he distinguishes between intuition (cognition not determined
by a previous cognition) and introspection (internal cognition not
determined by external cognition) and defends an account of knowledge
construed as a thoroughly mediated inferential sign process. A linchpin
of his argument is a methodological stance that favors any account of
mental activity that abides by the normal conventions of theory
construction, a stance which shifts the burden of proof to those
accounts wherein some special faculties are claimed for man. Peirce
concludes by adding as a novel seventh question some summary material
that appears at the end of "Questions concerning
Reality" dealing with some general arguments against the thesis
that there is no cognition not determined by a previous cognition.
There are two short pieces entitled "Potentia ex Impotentia"
also included here. These are early versions of beginnings of the second
published paper, "Some Consequences of Four Incapacities," and
again are interesting in their own right because of some methodological
points therein. First, Peirce makes the general comment that on the one
hand we should begin our philosophizing simply with those beliefs we
have no reason to call into question, but, on the other, we should not
maintain an attitude of certainty on matters concerning which there is
real disagreement among competent persons. In short, our philosophizing
should be continuous with our commonsense ways of dealing with the world
about us. Secondly, he makes a series of provocative statements about
the present state of philosophy and the methods of explanation that
should be employed in philosophy. The state of philosophy he likens to
the state of dynamics before Galileo; namely, a theater of disputation
and dialectics with little by way of established results. In this state,
he maintains, what is called for is not conservative caution (as would
have been called for in mechanics where much was truly established) but
rather bold and sweeping theorizing to break new ground and put the area
in order. Peirce does not mean that our metaphysical speculation should
be uncontrolled and irresponsible but that it should be guided by the
various different tangible facts we have at our disposal without any
pretense to demonstration, certainty, or finality. We should content
ourselves with the probable forms of reasoning that are so fruitful in
physical science and congratulate ourselves if we thereby reduce the
uncertainty in metaphysics to one hundred times that of these sciences.
It is in this spirit of speculation that one should view the sweeping
theory of mental activity he articulates in "Some Consequences of
Four Incapacities."
In the first published paper in this series Peirce had suggested, in
opposition to the Cartesian account, that all knowing involved an
inferential sign process. In the second paper in the series he takes up
the task of articulating in some detail his own theory of the structure
of mental activity, that is, the structure of the internal sign process
that is involved in knowing. Constructing this account, he is guided by
his methodological strictures to the effect that any account of the
internal (mental activity) must be in terms of the external (publicly
accessible objects) and that, given the postulation of one
structure,
another is not to be introduced into the theory unless there are facts
impossible to explain on the basis of the first.
Focusing on our
public sign system, that is, language, as the paradigmatic external
manifestation of mental activity, Peirce proceeds to construct an
account of mental activity in terms of "inner speech."
Furthermore, he develops an holistic form of this tradition in which the
basic mental unit is not the concept (the mental word) or even the
judgment (the mental sentence) but rather the process of reasoning
itself (the mental syllogism). Since it is then the structure (rather
than the matter) of the sign process that is of primary importance,
Peirce accordingly construes the process as one of drawing inferences,
as syllogistic in nature. Next, drawing on his formal accounts of
deduction, induction, and hypothesis, he proceeds to give an account not
only of thinking but also of the other forms of mental activity
(sensation, emotion, and attention) in terms of his syllogistic model.
His final extrapolation of the model enables him to give a speculative
account of the mind itself.
The third paper in the published
series, "Grounds of Validity of the Laws of Logic: Further
Consequences of Four Incapacities," picks up some of the remaining
questions outlined in MS 148 and finally comes to grips with Harris's
original challenge which had been the impetus for all three papers,
namely, how can Peirce account for the objective validity of the laws of
logic? The theories of cognition and reality were developed for the sake
of providing just such an account, an account which begins with a
justification of deduction and then broadens out to encompass a
philosophical grounding of the general logic of science.
The point of continuity with the previous pieces is Peirce’s claim that every cognition results from an inference and that the structure of all mental activity is inferential. Can't the question be raised-what reason do we have to believe that the principles of inference are true or correspond to anything in the real world? While not purporting to take seriously the stance of the absolute skeptic, Peirce does think it incumbent upon him to provide an account of the objective validity of the logical principles of inference. He proceeds to give an account of the validity of deduction, induction, and hypothesis; and his proffered "justifications" invoke the characteristic Peircean concepts of truth (as the ultimate agreement of investigators), reality (as that which is represented in that agreement), and community (as the ultimate ground of both logic and reality).
It would be difficult indeed to overstate the importance of these three papers in the Peircean corpus. That Peirce himself saw them as central is clear from his designation of them as Chapters 4, 5, and 6 of one of his major projected works, the 1893 "Search for a Method." Most later commentators have seen them as the key to his overall philosophical orientation.
III
Peirce’s "Description of a Notation for the Logic of Relatives, Resulting from an Amplification of Boole's Calculus of Logic" (DNLR) is one of the most important works in the history of modern logic, for it is the first attempt to expand Boole's algebra of logic to include the logic of relations. The complex mathematical analogies which govern parts of this work make it obscure in spots; but the main thrust of its important innovations may be seen by placing it in the context of Peirce’s earlier logical studies, and by relating it to the work of Boole, De Morgan, and Benjamin Peirce.
The logical substructure of
DNLR is a modified version of Boole's algebra of classes, in which
Peirce had shown an early interest.
15
One modification is the use of the
"inclusive" sense of logical addition, which Peirce had
introduced by 1867. 16
The other main modification is the replacement of
Boole's equality or identity sign (=) by the sign of illation or
inclusion ( -<) as the sign for the fundamental logical relation.
While this replacement may have been primarily dictated by formal
considerations, it was an important step on the road to a less algebraic
approach to the logic of classes.
To this basically Boolean
structure, Peirce adds a notation for relations and for operations upon
relations, as well as laws governing those operations. Even then,
though, the influence of Boole remains strong. While Peirce admits
logical relations between relations, he most often considers logical relations
that hold between class terms of
which relation terms form a part.
Peirce’s interest in the logic of
relations can be traced to several sources.
17 Published and unpublished
papers prepared around 1866 show a strong interest in the problems which
relation terms present for the theory of categories.
18 They are also
concerned with different types of relations, such as the distinction
between relations of equiparance and relations of disquiparance. His
work at this time also shows an interest in arguments involving
relations and multiple subsumptions. Such an argument is "Everyone
loves him whom he treats kindly; James treats John kindly; hence, James
loves John." Peirce’s early treatment of these arguments is rather
conservative, either reformulating them so as to apply the usual
syllogistic forms, or using some principle of multiple subsumption which
is construed as a natural generalization of the syllogism.
Unfortunately, the origins of the more powerful and, indeed, revolutionary techniques of DNLR are more obscure. 19 Only two surviving documents provide a sustained insight into their origins. One is the so-called Logic Notebook (LN), which carries entries from 3 to 15 November 1868 in which several notations are devised and some basic identities are shown. Only the rudiments of DNLR may be found here. The same is true of the other source, a series of notes that Peirce wrote at about the same time to add to a projected republication of his American Academy papers of 1867. Note 4 in this set shows how an algebraic notation may be used to validate the following argument, which De Morgan had claimed could not be shown to be valid by syllogistic means:
Every man is an animal.
Most unfortunately, the surviving parts of LN have no entries from 16 November 1868 through 5 October 1869, nor is there any other document which would allow us to trace the development of these techniques.
Peirce’s references to De Morgan in DNLR, as well as an undated
comparison (in LN) between his notation and De Morgan's, raise the
question of De Morgan's role in stimulating the work which led to
DNLR.20 It must be noted, though, that there is little direct
biographical information on this issue, and that Peirce’s later
recollections are contradictory and even inconsistent with known
facts.
Peirce apparently initiated an exchange of papers with De Morgan in late 1867, as a result of which De Morgan received a copy of Peirce’s "Three Papers on Logic" (the first three American Academy papers) by May 1868. In a letter dated 14 April 1868, De Morgan had promised to send Peirce a copy of his classic paper of 1860 on the logic of relations,21 but there is no direct evidence that this was ever sent. Nevertheless, Peirce had seen De Morgan's paper by late December 1868, since he refers to it in another paper sent to the printer at that time.22 It is thus very likely that Peirce had read De Morgan's paper before he wrote the entries in LN dated November 1868, even though those entries carry no clear references to De Morgan and use quite different examples.
Biographical issues aside, Peirce’s initial work in the logic of relations is significantly different from De Morgan's. The most important difference is that while De Morgan was interested primarily in the composition of relations with relations, Peirce is concerned with the composition of relations with classes. Thus, while De Morgan's paradigm is an expression such as "X is a lover of a servant of Y," Peirce is first concerned with such expressions as "lover of a woman." A predilection for class expressions is found even in DNLR, though this is often combined with the composition of relations, as in "lover of a servant of a woman." This emphasis upon class expressions seems to reflect the Boolean frame of reference in which Peirce was working.
De Morgan also considered two types of "quantified relations." The first is "X is an L of every M of Y," which is expressed by Peirce as "involution," or exponentiation. Even here, the LN shows him more concerned with the composition of a relation and a class, as in "lover of every woman," than with strictly relational composition. The other form of quantified relation is "X is an L of none but M of Y," a form which Peirce only considers in the section on "backward involution" which he added to DNLR shortly before it was printed (pp. 400-408).
These comparisons between De Morgan and Peirce make their relationship problematic. It becomes more so in view of the fact that some of De Morgan's most dramatic results involve the contrary and the converse of a relation. While Peirce deals with contraries throughout LN and DNLR, he did not consider converses in the 1868 portions of LN, and he only deals with them in that section of the DNLR which he added at the time of printing.
We may conclude that while Peirce probably knew of De Morgan's memoir on relations when he was working out the full notation of DNLR, his own Boolean orientation meant that he was working on these topics in his own way.
While DNLR is primarily a contribution to logic, parts of it may also be related to the developments in algebra to which his father contributed. During the years 1867-69, Benjamin Peirce presented a series of papers to the National Academy of Sciences which resulted in a book entitled Linear Associative Algebra (LAA) which was privately published in 1870, and then republished with notes by C. S. Peirce in 1881.23 ln it Benjamin Peirce surveyed all the types of linear associative algebras which can be constructed with up to seven units, enormously generalizing such algebras as that of complex numbers (of the form a • 1 + bi) and Hamilton's quaternions (a • 1 + bi + cj + dk). ln the subsection on Elementary Relatives in DNLR, Peirce conjectured that all linear associative algebras could be expressed in terms of elementary relatives, which he then proved in 1875 24 and illustrated in his notes to his father's book. This technique formed the foundation for the method of linear representation of matrices, which is now part of the standard treatment of the subject.
As in the case of the relationship of the DNLR to De Morgan's paper, its relation to his father's LAA is difficult to estimate accurately. Certainly they were working on these long papers at about the same time, so that some influence would not be surprising. ln a short letter to his father that has been dated 9 January 1870, Peirce writes:
"I think the following may possibly have some interest to you in connection with your algebras. I have been applying Boole's Calculus to the Logic of Relative Terms & in doing so have got (among other operations) an associative non commutative multiplication. It is like this. Let k denote killer, w wife, m man. Then
kwm denotes the class of killers of wives of men
The letter then concludes with the colleague-and-teacher example which is found in the Elementary Relatives section of DNLR (pp. 4O8-11). While this letter shows that Peirce was thinking of his father's work as he completed DNLR, it also suggests that the relationship between the two papers may not be very intimate.
DNLR was communicated to the American Academy of Arts and Sciences on 26 January 1870 and printed in the late spring. The exact time of its printing is uncertain, though it must have been printed by 17 June 1870 when Peirce left for Europe. He carried with him a letter of introduction from his father to De Morgan, to whom he apparently delivered copies of his memoir and his father's book. Although there is no contemporary record of Peirce’s visiting De Morgan, he planned to do so and recalled such a meeting in later years. But the meeting could not have been a very happy one, since De Morgan was in very poor health by that time and incapable of sustained logical or mathematical discussion.
The Boolean substructure of DNLR consists of inclusion and the usual Boolean operations of addition (x + y), multiplication (x,y), and class complementation (1 - x), along with their standard laws. To illustrate the relational notation, let s = servant, l = lover, and w = woman. The most important notations are relative multiplication (sl, servant of a lover), relative involution (sl, servant of every lover), backward involution (sl, servant of none but a lover), and converse of a relation (Ks, master). Invertible forms of several of these operations are also given. Relation expressions and class expressions may be combined, as in "SW" (servant of every woman) and "s(lw)" (servant of every lover of a woman). Boolean operations may be applied to relations as well as to classes, so that, for instance, "(S +, l)" means "either a servant or a lover."25
While DNLR is largely devoted to the logic of two-place relations, Peirce also includes a rather confusing discussion of "conjugative terms," which stand for three-place relations. This is a marked advance over De Morgan's restriction to two-place relations, but Peirce’s attempts to deal with this topic within the framework of DNLR present many problems of interpretation.
ln addition to outlining a notation, DNLR contains a great many principles which may be easily interpreted in the modern logic of relations. Some significant identities are
s(m +, w) = sm +, sw
(l +, s)w = lw +, sw
s,l = l,s
(sl)w - s(lw)
sm+,w - sm, sw
(s,l)w = sw,lw.
There are also a great many inclusions, such as
If a -< b then ca -< cb
If a -< b then cb -< ca,
along with chains of inclusions involving combinations of operations, as in
sw -< sw
and (ls)w -< lsw.
The complement of a relation is treated not only in a Boolean way, but also as an operation upon a relation, as is the operation of forming the converse of a relation. De Morgan's principles governing these operations are given in Peirce’s notation. The universal and null relations are introduced, and their laws are stated.
While Peirce does not attempt to develop the laws of his notation in a deductive manner, he does provide demonstrations of a sort for many of his laws, especially in the section entitled "General Method of Working with this Notation" (pp.387-417). In the first subsection on Individual Terms, many intuitively valid laws are demonstrated by reducing inclusions between classes to individual instances. ln addition to its discussion of backward involution and conversion, the subsection on Infinitesimal Relatives contains the most elaborate mathematical analogies in the memoir, with very puzzling applications of such mathematical techniques as functional differentiation and the summation of series. The subsection on Elementary Relatives relates his own work to Benjamin Peirce’s linear associative algebras.
For all its importance, the Logic of Relatives memoir presents many problems of interpretation. Perhaps the most serious issue is whether Peirce is dealing with relations or with relatives-that is, with the relation of being a servant, or with such classes as the class of servants or the class of servants of women. His choice of the term "relative" suggests a desire to distinguish his project from De Morgan's, but in some cases his terms clearly stand for relations. The situation is complicated by the fact that many terms, such as "servant," can stand for either a relation or a relative, depending upon the context. Perhaps it is safest to say that he deals with both relational and relative terms, but that he usually treats relational terms within the context of relative terms. While this seems true in general, the interpretation of particular formulas still remains puzzling.
Other serious issues concern his treatment of conjugative terms and his elaborate and obscure mathematical analogies. More generally, one may ask whether DNLR is best studied by translating it into standard symbolic logic or by considering it in its own right. With the benefit of hindsight, DNLR cries out for the modern theory of quantifiers, to which Peirce was to make important contributions. Nevertheless, the core of its notation is of considerable power and can be studied separately. It remains of interest to those modern logicians and mathematicians who have taken an algebraic approach to the study of logic. 26
MAX H. FISCH
1 Ben began a promising career as a mining engineer at Marquette, Michigan, but died near there at the early age of twenty-six, on 22 April 1870.
2 P. 288 below.
3Nevertheless, she married Edward H. Green later in 1867 and, as Hetty Green, was on her way to becoming "the witch of Wall Street."
41n the interim, from 1872 to 1890, there had been a small "Graduate Department" and Jem, as secretary of the Academic Council, had been its administrator.
5He later obtained and distributed collective offprints of the fourth and fifth papers.
6This is a good point at which to remind our readers that even a twenty-volume edition of Peirce’s writings is only an anthology, and that statements about his views based on the anthology may be falsified (or at least may seem to be falsified) by writings it omits. Our first volume, for very good reasons, omits MS 52 (921). If it had been included, it would have come between pages 33 and 37. Past the middle of it there is a leaf whose recto was headed at first "Of Realism & Nominalism. 1859 July 25." The "& Nominalism" was later deleted. The recto continues: "It is not that Realism is false; but only that the Realists did not advance in the spirit of the scientific age. Certainly our ideas are as real as our sensations. We talk of an unrealized idea. That idea has an existence as neumenon in our minds as certainly as its realization has such an existence out of our minds. They are in the same case. An idea I define to be the neumenon of a conception." That is all. But on the verso there is a "List of Horrid Things I am." They are: Realist, Materialist, Transcendentalist, Idealist. Why did Peirce delete "& Nominalism"? We can only guess. He was not yet twenty. Perhaps he had confused the sense of realism in which it is opposed to idealism with that in which it is opposed to nominalism, but settled on the former.
7 For details see Max H. Fisch, "Peirce’s Progress from Nominalism toward Realism," Monist 51(1967):159-78, at 160-65.
8For details see Max H. Fisch, "Peirce’s General Theory of Signs," in Sight, Sound, and Sense, edited by Thomas A. Sebeok (Bloomington: Indiana University Press, 1978), pp. 31-70 at 33-38 and, for Berkeley, pp. 57, 63, 65. For Peirce’s early nominalism and its probable derivation from Whately, see also pp. 60-63. (It is worth adding here that Boole in An Investigation of the Laws of Thought after an introductory first chapter begins the investigation with Chapter II "Of Signs in General, and of the Signs appropriate to the science of Logic in particular; also of the Laws to which that class of signs are Subject"; and that Chapter III is headed "Derivation of the Laws of the Symbols of Logic from the Laws of the Operations of the Human Mind.")
9Karl-Otto Apel, Charles S. Peirce: From Pragmatism to Pragmaticism, translated by John Michael Krois (Amherst: University of Massachusetts Press, 1981), pp. 53, 90, 153, 196, 213n107. Gerd Wartenberg, Logischer Sozialismus: Die Transformation der Kantschen Transzendenta/philosophie durch Charles S. Peirce (Frankfurt: Suhrkamp, 1971).
10John Fiske, Edward Livingston Youmans (New York: D. Appleton and Co., 1894), p. 340. (From a letter of Youmans reporting a visit with Clifford.)
11See part three of the present introduction, by Daniel D. Merrill, and the literature there referred to.
12At a meeting of the much older American Academy of Arts and Sciences on 12 October 1869, "Professor Peirce made a communication on his investigations in Linear Algebra."
13Cf. Carolyn Eisele, Studies in the Scientific and Mathematical Philosophy of Charles S. Peirce (The Hague: Mouton, 1979), pp. 58 f., 251 f., and The New Elements of Mathematics by Charles S. Peirce, edited by Carolyn Eisele (The Hague: Mouton, 1976), 3:xxiii-xxvii.
141t was probably Peirce’s intention to use the title "Questions concerning Reality" for his first published article, but Harris advised against this in a letter of about 15 April 1868, and Peirce replied on 20 April: "Your remark upon my title is very just. I will make it 'Questions concerning certain Faculties claimed for man'."
15 See Emily Michael, "An Examination of the Influence of Boole's Algebra on Peirce’s Development in Logic," Notre Dame Journal of Formal Logic 20(1979): 801-6.
16 See "On an Improvement in Boole's Calculus of Logic," item 2 below, pp.12-23.
17 See Emily Michael, "Peirce’s Early Study of the Logic of Relations, 1865-1867," Transactions of the Charles S. Peirce Society 10(1974):63-75.
I8 This interest culminates in "On a New List of Categories," item 4 below, pp. 49-59.
I9See Daniel D. Merrill, "De Morgan, Peirce and the Logic of Relations" Transactions of the Charles S. Peirce Society14(1978):247-84.
20Ibid. See also R. M. Martin, "Some Comments on De Morgan, Peirce, and the Logic of Relations," Transactions of the Charles S. Peirce Society12(1976):223-30.
21Augustus De Morgan, "On the Syllogism, No. IV, and on the Logic of Relations," Transactions of the Cambridge Philosophical Society 10(1864):331-58.
22"Grounds of Validity of the Laws of Logic: Further Consequences of Four Incapacities," item 23 below, pp. 242-72.
23American Journal of Mathematics 4(1881):97-229, and as a separate volume paged 1-133 (New York: D. Van Nostrand, 1882).
24"On the Application of Logical Analysis to Multiple Algebra," Proceedings of the American Academy of Arts and Sciences n.s. 2(1874-75):392-94, which will be published in volume 3 of the present edition.
25For analyses and interpretations of DNLR, see Chris Brink, "On
Peirce’s Notation for the Logic of Relatives," Transactions of
the Charles S. Peirce Society 14(1978):
285-304; R. M. Martin, "Of Servants, Lovers and Benefactors:
Peirce’s Algebra of Relatives of 1870," Journal of Philosophical
Logic 7(1978):27-48; Jacqueline Brunning, "Peirce’s Development of
the Algebra of Relations," diss. Toronto 1981; and Hans G.
Herzberger, "Peirce’s Remarkable Theorem," in Pragmatism and
Purpose: Essays Presented to Thomas A. Goudge Toronto:
University of Toronto Press, 1981), pp.41-58.
26Alfred Tarski, "On the Calculus of Relations," Journal of Symbolic Logic 6(1941):73-89.
The following corrections to the first printing have been incorporated in the second printing; the original readings are given in brackets.
thought [thought,]
a, b, [a , b]
n. [m.]
n [u]
est, aliud [est aliud,]
secundum [secundem]
antecedent [antecendent]
that no [that that]
it with [with it]
relatifs [relatives]
âge [age]
Hume [Hume’s]
magician [magican]
The annotation should be supplemented as follows:
Peirce’s “the memory” is “it” in the original, “compared with” is “in comparison of,” and “are” is “were.”
âge [age]
âge [age]
94.1–4 [194.1–4]
Emendations for errata 71 n. 3 l. 3, 227.2, 265.22, 312.21, and 485.14, which represent Peirce’s errors, have been added on pages 590, 608, 609, 614, and 627 respectively.
have come [come]
haec [hae]
informed depth [informed depth]
simple [Simple]
be ex- [be ex]
recognizing [reorganizing]
about 11 ¼ [about 11]
and [or]
it is [is]
Verse 20 in James Russell Lowell’s “Ode Recited at the Harvard Commemoration, July 21, 1865” [Not located, though there may be no such quotation.]
relatifs [relatives]
Dugald, [Dugal,]
“The question is, what is thought,—and the question can only be answered by means of thought.”
At the beginning of the period covered in Volume 3, Peirce was an active member of the famous Metaphysical Club in Cambridge, where in November 1872 pragmatism was probably born (as Max Fisch cautiously concluded in his introduction, W3: xxxi–xxxii). When cloudy weather prevented Peirce from engaging in photometric researches, he began drafting chapters of a projected logic book, some of whose chapters were dictated to two Coast Survey employees (Amanuensis A and Amanuensis B). A good quarter of the volume consists of 36 texts that are variant forms of eleven chapters intended for that unfinished book. They were written between the late winter or early spring of 1872 and the summer of 1873. The bulk of them work out the key ideas and arguments at the core of Peirce’s early pragmatism, including the distinction between doubt and belief, the four methods of settling opinion, what reality is, what meaning is, and the connection between reality, truth, and the final opinion.
Other more semiotic chapters analyze further the notion of representation and sign, the connection between the object of the cognition and the cognition itself, and especially the temporality of thought processes. And then a few essays make the link between logic and the study of signs, examine the copula of inclusion and the quasi-copula, study relative terms, and return to the theory of information in the context of the balance between logical breadth and depth.
Volume 3 also contains Peirce’s major 1873 paper “On the Theory of Errors of Observation,” a theory of which Peirce gives a general account, shows the limitations of the method of least squares, and how to remedy those limitations. Other scientific papers are related to Peirce’s research for the U.S. Coast Survey, whether they have to do with statistical considerations regarding rainfall, the principles of mechanics, or the flexibility of the pendulum support.
The brightest philosophical core of Volume 3 holds to the “anonymous” but public advent of pragmatism, which found its first published formulation in 1877–78 in Peirce’s Popular Science Monthly series titled “Illustrations of the Logic of Science”—anonymous because the term “pragmatism” does not appear in any of the six famous papers, “The Fixation of Belief,” “How to Make Our Ideas Clear,” “The Doctrine of Chances,” “The Probability of Induction,” “The Order of Nature,” and “Deduction, Induction, and Hypothesis.” (One has to wait until the year 1900 before finding the word “pragmatism” inscribed under Peirce’s own pen.) William James later testified that Peirce had frequently used the term “pragmatism” in conversation in the early 1870s to stand for the general theory of meaning developed in the first two “Illustrations,” the best known and most popular of all of Peirce’s writings.
The volume ends with three of the five chapters of the only book Peirce ever published, his 1878 Photometric Researches: Made in the Years 1872–1875, which represents the culmination of his astronomical work at the Harvard Observatory.
“How to give birth to those vital and procreative ideas which multiply into a thousand forms and diffuse themselves everywhere, advancing civilization and making the dignity of man, is an art not yet reduced to rules.”
“The question is, what is thought,—and the question can only be answered by means of thought.”
At the beginning of the period covered in Volume 3, Peirce was an active member of the famous Metaphysical Club in Cambridge, where in November 1872 pragmatism was probably born (as Max Fisch cautiously concluded in his introduction, W3: xxxi–xxxii). When cloudy weather prevented Peirce from engaging in photometric researches, he began drafting chapters of a projected logic book, some of whose chapters were dictated to two Coast Survey employees (Amanuensis A and Amanuensis B). A good quarter of the volume consists of 36 texts that are variant forms of eleven chapters intended for that unfinished book. They were written between the late winter or early spring of 1872 and the summer of 1873. The bulk of them work out the key ideas and arguments at the core of Peirce’s early pragmatism, including the distinction between doubt and belief, the four methods of settling opinion, what reality is, what meaning is, and the connection between reality, truth, and the final opinion.
Other more semiotic chapters analyze further the notion of representation and sign, the connection between the object of the cognition and the cognition itself, and especially the temporality of thought processes. And then a few essays make the link between logic and the study of signs, examine the copula of inclusion and the quasi-copula, study relative terms, and return to the theory of information in the context of the balance between logical breadth and depth.
Volume 3 also contains Peirce’s major 1873 paper “On the Theory of Errors of Observation,” a theory of which Peirce gives a general account, shows the limitations of the method of least squares, and how to remedy those limitations. Other scientific papers are related to Peirce’s research for the U.S. Coast Survey, whether they have to do with statistical considerations regarding rainfall, the principles of mechanics, or the flexibility of the pendulum support.
The brightest philosophical core of Volume 3 holds to the “anonymous” but public advent of pragmatism, which found its first published formulation in 1877–78 in Peirce’s Popular Science Monthly series titled “Illustrations of the Logic of Science”—anonymous because the term “pragmatism” does not appear in any of the six famous papers, “The Fixation of Belief,” “How to Make Our Ideas Clear,” “The Doctrine of Chances,” “The Probability of Induction,” “The Order of Nature,” and “Deduction, Induction, and Hypothesis.” (One has to wait until the year 1900 before finding the word “pragmatism” inscribed under Peirce’s own pen.) William James later testified that Peirce had frequently used the term “pragmatism” in conversation in the early 1870s to stand for the general theory of meaning developed in the first two “Illustrations,” the best known and most popular of all of Peirce’s writings.
The volume ends with three of the five chapters of the only book Peirce ever published, his 1878 Photometric Researches: Made in the Years 1872–1875, which represents the culmination of his astronomical work at the Harvard Observatory.
“How to give birth to those vital and procreative ideas which multiply into a thousand forms and diffuse themselves everywhere, advancing civilization and making the dignity of man, is an art not yet reduced to rules.”
| Preface | xi |
| Acknowledgments | xvii |
| Chronology | xix |
| Introduction | xxi |
|
1. Educational Text-Books, II | 1 |
| 2. [Lecture on Practical Logic] | 8 |
| 3. Third Lecture | 10 |
|
[TOWARD A LOGIC BOOK, 1872-73] | |
| 4. [Logic, Truth, and the Settlement of Opinion] | 14 |
| 5. [Investigation and the Settlement of Opinion] | 16 |
| 6. Chapter 1 | 18 |
| 7. Chapter 1 (Enlarged abstract) | 20 |
| 8. Chapter 1 (Enlarged abstract) | 21 |
| 9. Chapter 1. Of the Difference between Doubt and Belief | 22 |
| 10. Chapter 2. Of Inquiry | 23 |
| 11. Chapter 3. Four Methods of Settling Opinion | 24 |
| 12 [On Reality] | 28 |
| 13. Chapt. 4 (2nd draft) | 34 |
| 14. Chapt. 4 (----- draft) | 35 |
| 15. On Reality | 37 |
| 16. On Reality | 38 |
| 17. Chap. 4. Of Reality | 40 |
| 18. Of Reality | 47 |
| 19. Chapter IV. Of Reality | 54 |
| 20. Chapter IV. Of Reality | 60 |
| 21. Chapter ------. The list of Categories | 61 |
| 22. On Representations | 62 |
| 23. On Representations | 65 |
| 24. On the nature of signs | 66 |
| 25. [On Time and Thought] | 68 |
| 26. [On Time and Thought] | 72 |
| 27. Chap. 5th | 75 |
| 28. Chap. 6th | 77 |
| 29. Memorandum: Probable Subjects to be treated of | 81 |
| 30. Chap. 7. Of Logic as a Study of Signs | 82 |
| 31. Chap. 9th | 84 |
| 32. Chap. VIII. Of the Copula | 90 |
| 33. Chap. IX. Of relative terms | 93 |
| 34. Chap. X. The Copula and Simple Syllogism | 95 |
| 35. Chap. XI. On Logical Breadth and Depth | 98 |
| 36. Chapter IV. The Conception of Time essential in Logic | 102 |
| 37. Chapter IV. The Conception of Time essential in Logic | 105 |
| 38. Chapter V. That the significance of thoughtlies in its reference to the future | 107 |
| 39. Notes on Logic Book | 108 |
| 40. Letter, Peirce to Abraham B. Conger | 109 |
| 41. [On Errors of Observation] | 111 |
| 42. On the Theory of Errors of Observations | 114 |
| 43. Linear Associative Algebra: Improvement in the Classification of Vids | 161 |
| 44. Lazelle's One Law in Nature | 164 |
| 45. Rainfall | 167 |
| 46. [On Political Economy] | 173 |
| 47. On the Application of Logical Analysis to Multiple Algebra | 177 |
| 48. [Early Abstract of Photometric Researches] | 180 |
| 49. Notes on the Fundamentals of Algebra | 186 |
| 50. The Axioms of Geometry | 189 |
| 51. Logical Contraposition and Conversion | 191 |
| 52. Addition to the note for Mind | 195 |
| 53. Sketch of the Theory of Non-Associative Multiplication | 198 |
| 54. The Principles of Mechanics | 202 |
| 55. Nicholas St. John Green | 208 |
| 56. Note on the Sensation of Color | 211 |
| 57. On the Influence of the Flexibility of the Support on the Oscillation of a Pendulum | 217 |
| 58. On a New Class of Observations, suggested by the principles of Logic | 235 |
| 59. Note on Grassmann's Calculus of Extension | 238 |
|
ILLUSTRATIONS OF THE LOGIC OF SCIENCE | |
| 60. The Fixation of Belief | 242 |
| 61. How to Make Our Ideas Clear | 257 |
| 62. The Doctrine of Chances | 276 |
| 63. The Probability of Induction | 290 |
| 64. The Order of Nature | 306 |
| 65. Deduction, Induction, and Hypothesis | 323 |
| 66. Comment se fixe la croyance | 338 |
| 67. Comment rendre nos idees claires | 355 |
| 68. [Ferrero's Esposizione del metodo dei minimi quadrati] | 375 |
| 69. Photometric Researches | 382 |
| Editorial Notes | 495 |
| Bibliography of Peirce’s References | 541 |
| Chronological List, 1872-1878 | 546 |
|
TEXTUAL APPARATUS | |
| Essay on Editorial Method | 557 |
| Explanation of Symbols | 576 |
| Textual Notes | 578 |
| Emendations | 579 |
| Historical Collation | 606 |
| List of Variants | 611 |
| Word Division | 614 |
| Index | 617 |
There was no more intensively scientific seven-year period of Peirce’s life than that of the present volume. He had no academic employment and gave no lectures at Harvard or at the Lowell Institute or elsewhere. As an Assistant in the Coast Survey his duties had so far been astronomical, and his concurrent assistantship in the Harvard College Observatory (1869-72) had been arranged with a view to those duties. But from late in 1872 onward his duties became increasingly geodetic.
The Coast Survey, with help drawn from the Hydrographic Office of the Navy, was—and was recognized as—the chief scientific agency of the United States federal government. It had been founded in 1811. Its first Superintendent was Ferdinand Rudolph Hassler; its second was Alexander Dallas Bache (1843-67); its third, Benjamin Peirce, Charles's father (1867-74); and its fourth, Carlile P. Patterson (1874-81).
Until the creation of the Bureau of Standards in 1901, the Office of Weights and Measures was part of the Washington Office of the Coast Survey, and the Assistant in Charge of the Washington Office was in charge of the Weights and Measures Office also. Throughout the period of the present volume that Assistant was Julius E. Hilgard. In the summer of 1872 there was a conference in Paris looking toward the creation of an international bureau of weights and measures there. Hilgard was given an extended leave of absence to attend that conference and for other purposes. From 15 April to 23 August, Charles Peirce was Acting Assistant in Charge of the Survey's Washington Office. The records of his "photometric researches" show that he was in Washington for several further months in that and succeeding years.
The present volume includes a number of chapter drafts of what we have called "Toward a Logic Book, 1872-73." Concerning these, he wrote to his mother from Washington on 20 April 1872: "On clear nights I observe with the photometer; on cloudy nights I write my book on logic which the world has been so long & so anxiously expecting." The book was never finished. Neither were the related "Illustrations of the Logic of Science" of 1877-78, which were advertised as a book in preparation for the International Scientific Series. The six papers he did finish and publish would not have made much more than half the intended book.
The Coast Survey was the chief scientific agency of the federal government not only in its own researches but also, especially during the superintendencies of Bache and Benjamin Peirce, in the help it gave to scientists not in its employ. The most widely known example of this began in December 1871 and continued into the fall of 1872. Peirce had named two of the Survey's new vessels after Hassler and Bache and had assigned the Bache to the Atlantic coast and the Hassler to the Pacific. To get to our Pacific coast, the Hassler had to travel around South America. Dear to the heart of Benjamin Peirce’s friend, Louis Agassiz, was the Museum of Comparative Zoology at Harvard, and the Hassler's voyage would be a great opportunity to add to its collections. But Agassiz was the chief American opponent of Darwin's theory of evolution, and the voyage of the Hassler would take him, late in life, on the nearest approach to Darwin's early-in-life five-year voyage of the Beagle that could be carried out in less than a year. He gladly accepted Superintendent Peirce’s invitation, as did his wife and ex-president Thomas Hill of Harvard.
The Hassler sailed on 4 December 1871. In The American Naturalist for January 1872 there appeared a letter from Agassiz to Superintendent Peirce "Concerning Deep-Sea Dredgings" dated 2 December 1871, in which he discussed the questions he hoped the voyage would help to answer, including Benjamin's own theory of "continental drift."
The Survey's own scientific representative on the voyage was Agassiz's former pupil, Assistant Louis Francois de Pourtales. The few books they took along were chiefly by Darwin, including of course his Voyage of the Beagle. Darwin was informed of the plan well in advance and sent his best wishes. The captain of the Hassler was Philip C. Johnson, and there were occasional comparisons between him and Captain FitzRoy of the Beagle. The deep- sea dredging equipment of the Hassler proved defective, and that was a great disappointment; but dredging at moderate depths resulted in numerous and important additions to the collections of the Harvard Museum of Comparative Zoology. Johnson, Agassiz, and Pourtales sent reports to Superintendent Peirce along the way. Mrs. Agassiz sent the Atlantic Monthly an article which appeared in its October 1872 issue, and she had two further articles in the January and March 1873 issues. The best day-by-day account was by Pourtales, in Appendix 11 of the 1872 Coast Survey Report.
Under Agassiz's direction, his wife kept a journal of scientific and personal experience which was nearly ready for publication at the time of his death in 1873. She drew upon it for the account of the expedition which she included in her Louis Agassiz His Life and Correspondence, published in 1885.
Chauncey Wright, the most vigorous defender of Darwin among the members of the Metaphysical Club in Cambridge, had had a long article on "The Genesis of Species" in the North American Review for July 1871, which had pleased Darwin so much that, with Wright's permission, he had it reprinted in pamphlet form in England. Wright visited Darwin at Down, 4 -5 September 1872, four days after the Hassler reached San Francisco.
That was the end of the Hassler's voyage. The captain and crew remained, and the passengers returned by the recently completed transcontinental railway. The Agassizs first lingered for a while, and he addressed gatherings of the California Academy of Sciences; but they were back in Cambridge by October. And by November, Chauncey Wright was back from his European travels and his visit with the Darwins.
It is quite likely, therefore, that the Metaphysical Club in Cambridge had already devoted some of its meetings to the Darwinian theory of evolution, and not altogether unlikely that Peirce at the meeting he addressed in November 1872 presented his pragmatism as the lesson in logic taught by Darwin's Origin of Species, as he certainly did in "The Fixation of Belief" in 1877 and in "Comment se fixe la croyance" in 1878.
The Coast and Geodetic Survey
The most decisive single step of Benjamin Peirce’s superintendency of the Coast Survey had already been taken in March 1871, when he obtained an act of Congress authorizing a transcontinental geodetic connection along the 39th parallel between the Atlantic and Pacific coastal surveys, along with a small initial appropriation. The fundamental problem of geodesy was that of the figure of the earth, and the chief instruments for its determination were gravity pendulums.
The first international scientific association was geodetic. Its founding conference had been at Berlin in 1864. In the French form of its name, it was called international from the beginning. In the German form, it was called at first middle-European, then European, and only in 1886 did it begin to be called international. Conferences were held every third year, but there was a "Permanent Commission" or standing executive committee that met annually. There was also a Special Committee on the Pendulum. By 1872 the association was settling on the Repsold-Bessel reversible pendulum as the best research instrument for its principal purpose.
On 30 November 1872 Superintendent Peirce wrote Assistant Peirce a letter of instructions beginning: "You are hereby directed to take charge of the Pendulum experiments of the Coast Survey, and to direct and inspect all parties engaged in such experiments. ... In combination with the pendulum experiments you will investigate the law of the deviations of the plumb line and of the azimuths from the spheroidal theory of the earth's figure."
Since this assignment would involve spending most of his time away from Cambridge, Charles resigned his assistantship in the Harvard College Observatory on 2 December 1872.
Ten days later Charles wrote to A. & G. Repsold and Sons in Hamburg, Germany, ordering for the Coast Survey one of their reversible pendulums suitable for absolute determinations of gravity. The Repsolds replied that there would be a delay in filling the order because they had such an accumulation of still unfilled orders for other instruments to be used in observing the transits of Venus in 1874 and 1882. (The last previous transits had been in 1761 and 1769. The next would be in 2004 and 2012.) The pendulum was finally ready in the spring of 1875.
Meanwhile, in 1873 and 1874, Charles conducted parties making observations of gravity with nonreversible, invariable pendulums with conical bobs, on Hoosac Mountain and in the Hoosac Tunnel in northwestern Massachusetts, and at Northampton and Cambridge. During the same extended periods, and for the most part with the same aides, he continued the photometric researches which he had already begun in Cambridge and in Washington earlier in 1872, using a Zollner astrophotometer attached to a telescope inside a portable observatory, with an aide outside recording his observations. He had also, but under conditions too unfavorable, tried the experiment of "weighing the earth" at the top and bottom of the central shaft of the Hoosac Tunnel.
By 1875, the greater part of the photometric researches was completed, but he wanted still to make a more thorough study of earlier star catalogues. During his second Coast Survey assignment in Europe (1875-76), he examined medieval and renaissance manuscripts of Ptolemy's star catalogue in several libraries. He also made inquiries as to the methods used in the preparation of the most recent star catalogue, the Durchmusterung of Argelander and SchOnfeld at the Bonn Observatory. Peirce’s hook, Photometric Re-searches (1878), included his own edition of Ptolemy's catalogue, as well as a long letter from Schonfeld concerning the methods of the Durchmusterung
The chief purpose of this second sojourn, however, was to accept delivery from A. & G. Repsold and Sons in Hamburg of the reversible pendulum, and to make such determinations at so-called "initial stations" in Europe; namely, those at Berlin, Geneva, Paris, and Kew. In April 1875 at the new Cavendish Laboratory in Cambridge, England, he consulted Maxwell about the theory of the pendulum. At Hamburg in late May and early June, he took possession of the Repsold pendulum and made preliminary tests of it. He then conferred in Berlin with General Baeyer, founder and president of the Royal Prussian Geodetic Institute, who questioned the stability of the Repsold stand. Peirce went next to Geneva. By arrangement with Professor Plantamour, Director of the Observatory, he swung his new pendulum there, and detected and measured the flexure of the stand that General Baeyer had suspected.
In September 1875, the Permanent Commission of the International Geodetic Association met for ten days in Paris. On one of those days there was also a meeting of the Special Committee on the Pendulum, at which Peirce reported his Geneva findings. The Special Committee reported to the Permanent Commission. Peirce took part in the discussion of its report. He thus became the first invited American participant in the committee meetings of an international scientific association.
Later in 1875 and in 1876, Peirce swung his new pendulum for extended periods in Paris, in Berlin, and at Kew; and after his return to the United States, at the Stevens Institute in Hoboken. The Coast Survey Report for the year 1876 (not published until 1879) contained 145 pages by Peirce on "Measurements of Gravity at Initial Stations in America and Europe," on the second page of which he said: "The value of gravity-determinations depends upon their being bound together, each with all the others which have been made anywhere upon the earth.... Geodesy is the one science the successful prosecution of which absolutely depends upon international solidarity."
(Making the Stevens Institute at Hoboken the "initial station" for the United States involved months of pendulum swinging there and, for that purpose as well as for readier access to Washington and other sites, Peirce took up residence in New York City. His wife Zina had her own commitments in Cambridge and Boston, and declined to accompany him. They were never reunited. By far the fullest and best account of her, and of Charles in his relations with her and with other members of her family, is Norma P. Atkinson's 1983 doctoral dissertation, "An Examination of the Life and Thought of Zina Fay Peirce, an American Reformer and Feminist.")
The next general conference of the International Geodetic Association was held at Stuttgart in late September and early October of 1877. By invitation, Peirce had sent well in advance a memoir in French on the effect of flexure of the Repsold stand on the oscillations of the reversible pendulum. This memoir, lithograph copies of which had been distributed in advance of the conference, and papers by Plantamour and his colleague Cellerier confirming Peirce’s findings were published as appendixes to the proceedings of the conference. Peirce attended the conference as accredited representative of the United States Coast Survey. That was the first formal representation of an American scientific agency in the sessions of an international scientific association. During the discussions, Herve' Faye, president of the Bureau of Longitudes in Paris, suggested that swaying of the stand could be prevented by swinging from the same stand two pendulums with equal amplitudes but in opposite phases. Peirce later made an analytic mechanical investigation of Faye's proposal, concluding that it was as sound as it was brilliant. Copies of this investigation were distributed at the 1879 meeting of the Permanent Commission.
Peirce was active in still other fields that called for international cooperation. One of these was metrology. In 1872 when Peirce was Acting Assistant in Charge of the Coast Survey's Washington Office, he had control of the United States Office of Weights and Measures, a department of the Coast Survey until 1901. The American Metro-logical Society had been founded in 1873, and two years later, Peirce had become a member of its Committee on Units of Force and Energy. When he was elected to the National Academy of Sciences in April 1877, he was immediately made a member of its Committee on Weights, Measures, and Coinage.
Before his election to membership, he had received grants from the Bache Fund of the National Academy for the experiments reported in his "Note on the Sensation of Color," which was published in 1877 both in this country and in England, and which made him the first modern experimental psychologist on the American continent.
Of the thirty-four papers that Peirce presented to the National Academy of Sciences in the thirty-three years from November 1878 to November 1911, the first was geodetic: "On the Acceleration of Gravity at Initial Stations."
There was in Washington, besides the National Academy of Sciences, what called itself "The Philosophical Society of Washington." In its name, as in that of the American Philosophical Society in Philadelphia (established in 1743), "Philosophical" meant "Scientific." Benjamin Peirce had been one of the founders of both the Academy and the Society. Charles was elected a member of the latter on 1 March 1873. From 1871 to 1874 he presented the following papers:
16 December 1871: On the Appearance of Encke's Comet as Seen at Harvard College Observatory
19 October 1872: On Stellar Photometry
21 December 1872: On the Coincidence of the Geographical Distribution of Rainfall and of Illiteracy, as shown by the Statistical Maps of the Ninth Census Reports
17 May 1873: On Logical Algebra
3 January 1874: On Quaternions, as Developed from the General Theory of the Logic of Relatives
14 March 1874: On Various Hypotheses in Reference to Space.
Charles continued to make presentations to the American Academy of Arts and Sciences in Boston (some of which were published in its Proceedings), but they were now predominantly scientific:
12 March 1872: On Stellar Photometry (exhibiting the Zollner astrophotometer)
9 March 1875: Photometric Measurements of the Stars
11 May 1875: On the Application of Logical Analysis to Multiple Algebra [At this meeting his father presented a paper "On the Uses and Transformations of Linear Algebra."]
11 October 1876: On a new edition of Ptolemy's Catalogue of Stars
10 October 1877: Note on Grassmann's Calculus of Extension
13 March 1878: On the Influence of Internal Friction upon the Correction of the Length of the Second's Pendulum for the Flexibility of the Support
11 June 1879: On the Reference of the Unit of Length to the Wave-Lengths of Light.
We return now to the theme of this section of the present introduction. What opened the way to the breadth and intensity of Peirce’s scientific work in the period of the present volume? His father's initiative in beginning the transcontinental geodetic survey, and that of Superintendent Patterson in continuing it. Patterson in 1878 obtained an act of Congress changing the Survey's name to: The Coast and Geodetic Survey. The transcontinental survey was finally completed in the late 1890s. Meanwhile, the survey of the Atlantic and Gulf coasts had gradually been transformed by connecting it with a geodetic survey along the "eastern oblique arc" from Calais in Maine to New Orleans. (Peirce’s own first year with the Survey, 1859-60, had taken him to both ends of this arc.)
Both surveys were finally completed in the late 1890s, were edited by Assistant Charles A. Schott, and were published in 1900 (871 quarto pages) and 1902 (394 quarto pages) under the titles The Trans-continental Triangulation and the American Arc of the Parallel and The Eastern Oblique Arc of the United States and Osculating Spheroid. These are two classics of the science of geodesy. Peirce’s own connection with the Survey had ceased at the end of 1891, but he drafted a review of them, with emphasis on the latter. If that review had been carefully revised and published, it would itself rank as a milepost in the history of geodesy. (It should be added that, at the time Peirce drafted this review, work was beginning on the geodetic survey of the 98th meridian, which runs from eastern North Dakota through South Dakota, Nebraska, Kansas, Oklahoma, to a point not far from the southernmost tip of Texas. Obviously this was chosen as the longest nearly central meridian.)
Peirce was not merely a philosopher or a logician who had read up on science. He was a full-fledged professional scientist, who carried into all his work the concerns of the philosopher and logician. So when, for example, he wrote his "Illustrations of the Logic of Science," which moved rapidly to questions of statistics and probability, he had already made professional contributions to precisely those fields. At almost the same time, it was as a professional statistician that he reviewed his Italian friend Ferrero's book on the method of least squares in the first issue of the American Journal of Mathematics.
The Metaphysical Club and the Birth of Pragmatism
In the first part of the introduction to volume 2 of this edition we presented evidence for concluding that Peirce was a nominalist at first, and that his first steps toward realism were taken in his Journal of Speculative Philosophy articles of 1868-69 and in his Berkeley review of 1871. The essential element in these steps was giving 'real' and 'reality' a forward rather than a backward reference. The natural and logical next step, we said, was the pragmatism that, according to James and Peirce in recollections of a quarter of a century later, was born in the Metaphysical Club in the early 1870s.
Of all the papers in the present volume, the one so far most often referred to has been that of January 1878, "How to Make Our Ideas Clear," and its oftenest quoted paragraph is: "It appears, then, that the rule for attaining the third grade of clearness of apprehension is as follows: Consider what effects, which might conceivably have practical bearings, we conceive the object of our conception to have. Then, our conception of these effects is the whole of our conception of the object."
It was over twenty years later, in September 1898, in William James's "Philosophical Conceptions and Practical Results," that "pragmatism" first appeared in print as the name for this rule; but James said there that Peirce had called it "the principle of . . . pragmatism... when I first heard him enunciate it at Cambridge in the early '70's." James says nothing of the occasion for its enunciation, but we shall find reason below to conclude, at least tentatively, that it was a meeting of the Metaphysical Club not later than November 1872.
As late as 1909 Peirce was revising the "Illustrations of the Logic of Science" to reappear at last in book form, with revisions of the first two papers presented as two parts of a single paper to be entitled "My Pragmatism." Drafts of the preface to the projected volume, which never reached publication, contain the fullest surviving comparison between the Metaphysical Club paper of 1872 and the first two "Illustrations" of 1877-78.
We cannot identify the Club paper with any known surviving manuscript, but, on the hypothesis that there was such a paper, we may turn to what we have called "Toward a Logic Book, 1872-73" and ask ourselves how much of it anticipates the first two "Illustrations." Item 9 in our table of contents, written between 11 and 14 May 1872, will then give us some idea how close the correspondence between the Club paper and the first two "Illustrations" might have been. It may next strike us that the applications of the maxim in "How to Make Our Ideas Clear" to the ideas of hardness, weight, and force are there for the sake of its application to the idea of reality; and we may then reread the different versions of a chapter on "Reality" in "Toward a Logic Book" with heightened interest. We should then be ready to interpret and evaluate the remark at the end of the first part of the introduction to volume 2, that pragmatism was the natural and logical next step from the forward reference of the idea of reality in the Journal of Speculative Philosophy articles and the Berkeley review.
Our earliest evidence of the Metaphysical Club's existence is in two letters of Henry James, William's younger brother, in January and February 1872, to friends then living in Europe. From these letters alone we might guess that the Club had been founded after Peirce’s return from Washington in January. Peirce himself often assigns it an earlier beginning, soon after his return from Europe in the spring of 1871. Perhaps the founding had been preceded by informal gatherings of some of the same people. Henry James mentions Chauncey Wright, Peirce, Oliver Wendell Holmes, Jr., William James, and "various other long-headed youths" who "wrangle grimly & stick to the question."1
To the four members named by Henry James, Peirce in later recollections adds Nicholas St. John Green, Francis Ellingwood Abbot, John Fiske, Henry Ware Putnam, Francis Greenwood Peabody, William Pepperell Montague, and Joseph Bangs Warner. (Within the year 1872 Green and Wright reached the age of 42, Abbot 36, Peirce 33, Holmes 31, James and Fiske 30, Putnam and Peabody 25, Montague and Warner 24.) Peabody and Warner had attended Peirce’s lectures on British Logicians in 1869-70 and had studied Kant with him privately. They had also attended Fiske's lectures, which had immediately preceded Peirce’s Abbot had been a Harvard classmate of Peirce’s With the possible exception of Putnam, all ten were important figures in Peirce’s life. From his under-graduate years he had known Wright, a bit less than nine years older than he. His acquaintance with James had begun when they were in the Lawrence Scientific School together. James's family had moved to Cambridge in the fall of 1866. Their home was on Quincy Street, across from the Harvard Yard, about where the Faculty Club now stands. Peirce’s review of The Secret of Sweden Swendenborg, by James's father, was included in our second volume. James and Holmes had attended some of Peirce’s Lowell Lectures (included in our first volume) together in the fall of 1866. Holmes's father had been a Harvard classmate of Peirce’s father, and they were fellow members of the Saturday Club. When Peirce’s father died in 1880, Holmes's father wrote the poem in his honor that appeared in the Atlantic Monthly.
The most striking fact about the eleven members named by Peirce is that more than half of them were lawyers. (Only three were scientists-Wright, Peirce, and James, who was then teaching anatomy and physiology; two were theologians-Abbot and Peabody; the remaining six were lawyers, and of these all but Fiske were lifelong lawyers.) And the most striking remark that Peirce later makes about the birth of pragmatism in the Club is that, while acknowledging the paternity that James had already ascribed to him, he calls lawyer Green its grandfather, because Green had so often urged the importance of applying Alexander Bain's definition of belief as "that upon which a man is prepared to act," from which "pragmatism is scarce more than a corollary."
Since it is in letters from Henry James to friends in Europe that we first hear of the Metaphysical Club, it is a matter of interest that it was in a letter to Henry after Henry's own return to Europe that William James wrote on 24 November 1872: "Chas. Peirce . . . read us an admirable introductory chapter to his book on logic the other day."2 Thomas Sergeant Perry wanted it for the North American Review, in which Peirce’s Berkeley review had appeared in the previous year; but Peirce thought it not suitable for the Review, perhaps because it was too technical or assumed too much that had been argued out in the Club. This was probably the occasion recalled by James in 1898 as that on which Peirce enunciated the principle of pragmatism and called it by that name.
Fiske died in 1901. Perry was working on a short biography of him in 1905. James wrote Perry on 24 August: "If you want an extra anecdote, you might tell how, when Chauncey Wright, Chas. Peirce, St. John Green, Warner and I appointed an evening to discuss the 'Cosmic Philosophy,' just out, J. F. went to sleep under our noses."3 That would have been in November 1874. Wright died 12 September 1875. Peirce was in Europe then. James wrote the obituary for The Nation. On 10 February 1876, James wrote to his brother Robertson James: .... . we have reorganized a metaphysical club here."4 The other members of the original Metaphysical Club it included were Green, Holmes, Fiske, Warner, and Abbot. Peirce was still in Europe, and he never resumed residence in Cambridge. Green died 8 September 1876, less than a year after Wright. Without Wright and Green, and without Peirce, the reorganized metaphysical club may not have borne much resemblance to the one in which pragmatism was born.
But, whether for the original or for the reorganized club, why the name "Metaphysical" rather than "Philosophical?" Negatively, because "philosophical" still meant scientific, as in the old American Philosophical Society in Philadelphia or in the new Philosophical Society of Washington. Positively, because the most famous club in the world that was philosophical in our sense was the Metaphysical Society in London, which had been founded in 1869. Many papers presented to that Society had already appeared in the Contemporary Review in 1870 and 1871. Peirce had spent several weeks in London in July 1870 and in February 1871, and his father had been there in October 1870 and in January 1871. They can scarcely have failed to hear of the Society.5
Back now to Holmes and the law-dominated Metaphysical Club in Cambridge. In the spring of 1872 Holmes gave a course of twelve University Lectures on Jurisprudence, with Austin's Lectures on Jurisprudence as text. Though we have so far no evidence of such a meeting, it seems likely that at least one meeting of the Metaphysical Club that spring was devoted to discussion of the main argument of Holmes's lectures. Holmes became the sole editor of the American Law Review beginning with the July 1872 issue. In that issue, in a notice of an article by Frederick Pollock criticizing Austin in the April number of Law Magazine and Review, Holmes included a summary of his own lectures. Taking a different tack from Pollock's, he pushed to its logical conclusion Austin's view that custom only becomes law by the tacit consent of the sovereign manifested by its adoption by the courts, and that before its adoption it is only a motive for decision. What more, Holmes asked, is the decision itself in relation to any future decision?
What more indeed is a statute; and in what other sense law, than that we believe that the motive which we think that it offers to the judges will prevail, and will induce them to decide a certain case in a certain way, and so shape our conduct on that anticipation? A precedent may not be followed; a statute may be emptied of its contents by construction, or may be repealed without a saving clause after we have acted on it; but we expect the reverse, and if our expectations come true, we say that we have been subject to law in the matter in hand.
It must be remembered . . . that in a civilized state it is not the will of the sovereign that makes lawyers' law, even when that is its source, but what a body of subjects, namely, the judges, by whom it is enforced, say is his will. The judges have other motives for decision, outside their own arbitrary will, beside the commands of their sovereign. And whether those other motives are, or are not, equally compulsory, is immaterial, if they are sufficiently likely to prevail to afford a ground for prediction. The only question for the lawyer is, how will the judges act? Any motive for their action, be it constitution, statute, custom, or precedent, which can be relied upon as likely in the generality of cases to prevail, is worthy of consideration as one of the sources of law, in a treatise on jurisprudence. Singular motives . . . are not a ground of prediction, and are therefore not considered.6
This predictive theory remained the most prominent feature of Holmes's philosophy of law. His fullest and best exposition of it was in "The Path of the Law" in 1897. It has since come to be called "legal pragmatism." Accepting that name for it, we remark that legal pragmatism was in print five and a half years before logical pragmatism. And even if Peirce had permitted Perry to publish his Metaphysical Club paper in the North American Review, logical pragmatism would have been, at the very least, six months behind legal pragmatism in reaching print.
It is often asserted or assumed that Peirce had little or no interest in law, in the philosophy of law, or even in political or social philosophy; but we know that, at least by the end of 1871, he was intensely interested in mathematical economics; we have his wife Zina's reports of his advocacy of proportional representation; she was president of the first Woman's Parliament in 1869; his mother's father had been a lawyer, founder of one of the earliest law schools in the country and U.S. Senator from Massachusetts; his father's mother would have married lawyer Joseph Story, later Justice of the Supreme Court, if her parents had not dissuaded her; his own father was a leading member of the American Social Science Association (which antedated the more specialized social science associations) and was chairman of its Department of Education from 1869 to 1872; Charles and his father had been expert witnesses in the famous Howland will case in 1867; his older brother "Jem" J. M.) had spent a year in the Harvard Law School; his younger brother Herbert went into diplomacy and became our Minister to Norway; and his own vividest recollections of the Metaphysical Club are of its oldest member, lawyer Green.
To Baldwin's Dictionary of Philosophy and Psychology, in 1902, Peirce contributed the article "Proximate," the principal section of which is on "proximate cause and effect" and derives from Green's "Proximate and Remote Cause," the leading article in the January 1870 American Law Review, of which Holmes was already co-editor. Thirty-one years later, this article was the first in the collection of Green's papers edited by his lawyer son under the title Essays and Notes on the Law of Tort and Crime (1933). Twenty-one years still later, it appeared a third time as an appendix to Jerome Frank's "A Conflict with Oblivion" as evidence that Holmes's philosophy of law derived from Green's, and hence that "Green was the grandfather not only of Pragmatism in general but of legal Pragmatism as well."7
In 1958 the Journal of Public Law published a symposium of three papers on Peirce, followed by a reprinting of his 1892 article "Dmesis," introduced as "one of the very few writings in which this philosopher deals directly with law."8 It was also the article in which he had come closest to the words he put into Green's mouth seventeen years later, in those vividest recollections of the Metaphysical Club mentioned above.
Our purpose in looking so far beyond the present volume's years is only to encourage readers interested in the philosophy of law and in social philosophy more generally to be on the lookout for them and to expect to find them in this and in preceding and later volumes. (For brief examples in our two preceding volumes, see 1:339 and 399, and 2:464 and 465.)
One last bit of evidence: When Peirce was elected a member of the American Academy of Arts and Sciences in 1867, he was assigned to Class III, Moral and Political Sciences, Section I, Philosophy and Jurisprudence. When Green was elected at the end of November 1872, shortly after Peirce’s Metaphysical Club paper was presented, he was assigned to the same class and section; and so was Holmes when he was elected in 1877. Wright had long been a member of Class I, Mathematical and Physical Sciences, Section I, Mathematics. When James was elected in 1875, he was assigned to still another class and section.
One of the striking differences between the 1872-73 chapter drafts toward a logic book and the 1877-78 "Illustrations of the Logic of Science" is the prominence of the theory of signs in the former and its absence from the latter. An obvious though not a conclusive explanation is (1) that none of the chapter drafts on representations or signs seems to have been intended as the first, or even as a very early, chapter in the logic book, and (2) that the "Illustrations" were never completed.
What are the evidences of the incompleteness? (a) The forward references to topics that the six papers do not reach. (b) The last words of the third paper: "at this early stage of our studies of the logic of science." Half way through a series of six papers is not an "early stage." (c) The readers of the Popular Science Monthly were given no hint that the sixth paper was to be, or had been, the last. (d) The publishers of the Monthly were also the publishers of the International Scientific Series, and among the volumes they advertised as in preparation was Illustrations of the Logic of Science by Charles S. Peirce; but the six papers would not have made much more than half a volume. (e) Early in 1881 Peirce wrote to his mother: "I am thinking of undertaking some more papers for the Popular Science Monthly though I can hardly screw myself up to that point yet."
That further "Illustrations" would still have been welcomed and published was assured by the fact that their importance had been recognized by G. Stanley Hall in his article in Mind for January 1879 on "Philosophy in the United States." He gave greatest space to them, assumed there were more to come, and said they promised to be "one of the most important of American contributions to philosophy."
The incompleteness of the "Illustrations" is the obvious answer to the question: "If pragmatism is the lesson in logic taught by Darwin's Origin of Species, why does Peirce never get back to Darwin and the Origin?" We may ask ourselves, "If he had got back, what would he have said?" And we may remind ourselves that in his published opening lecture at The Johns Hopkins University in September 1882 he said, among other things: "The scientific specialists—pendulum swingers and the like—are doing a great and useful work; each one very little, but altogether something vast. But the higher places in science in the coming years are for those who succeed in adapting the methods of one science to the investigation of another. That is what the greatest progress of the passing generation has consisted in. Darwin adapted to biology the methods of Malthus and the economists."
And in 1909, five years from the end of his life, in revising the third and fourth "Illustrations," he wrote that when the Origin reached Cambridge early in the winter of 1859, he was with a Survey party on the east coast of Louisiana. A letter from his mother told him what a sensation the book had made; and thereupon "I wrote to my friend Mr. Chauncey Wright that I felt confident that Darwin had received a hint of his idea from Malthus On Population."
A better answer would be the paper on "Design and Chance" that he presented to the Metaphysical Club at The Johns Hopkins University in 1884, and thus got back to the Origin at greatest length, by way of honoring its twenty-fifth anniversary.
But, even without their intended continuation, the six "Illustrations" that were published in 1877-78 have gradually come to be recognized as the nineteenth century Discourse on the Method of Rightly Conducting the Reason and Searching for the Truth in the Sciences; and so far no twentieth century Discourse has superseded it.9
—MAX H. FISCH
1. Henry James Letters, edited by Leon Edel (Cambridge: Harvard University Press, 1974), I:273. Cf. p.269.
2. Ralph Barton Perry, The Thought and Character of William James (Boston:
Little, Brown, and Co., 1935), I:332.
3. Henry James, The Letters of William James (London: Longmans, Green, and Co.,1920), I1:233.
4. Perry, Thought and Character, I:713.
5. See Alan Willard Brown, The Metaphysical Society: Victorian Minds in Crisis,
1869-1880 (New York: Columbia University Press, 1947).
6. American Law Review 6 (1872): 724. (Reprinted in Frederic Rogers Kellogg, The Formative Essays of Justice Holmes: The Making of an American Legal Philosophy [Westport, CT: Greenwood Press, 1984], p.92.)
7. Jerome Frank, "A Conflict with Oblivion: Some Observations on the Founders of Legal Pragmatism," Rutgers Law Review 9 (1954): 425-63.
8. Journal of Public Law 7 (1958): 30-36. Cf. CP 2.164 (1902).
9. For more detailed discussions and further evidence regarding several of the points made in the third part of this introduction, see the following essays: "Justice Holmes, the Prediction Theory of Law, and Pragmatism," Journal of Philosophy 39 (1942): 85-97; "Alexander Bain and the Genealogy of Pragmatism," Journal of the History of Ideas 15 (1954): 41344; "Philosophical Clubs in Cambridge and Boston," Coranto 2 (1964): 12-23; "Was There a Metaphysical Club in Cambridge?" in Studies in the Philosophy of Charles Sanders Peirce Second Series, edited by Edward C. Moore and Richard S. Robin (Amherst: University of Massachusetts Press, 1964), pp. 3-32, and "Was There a Metaphysical Club in Cambridge?-A Postscript," Transactions of the Charles S. Peirce Society 17 (1981): 128-30; and "American Pragmatism Before and After 1898," in American Philosophy from Edwards to Quine," edited by Robert W. Shahan and Kenneth R. Merrill (Norman: University of Oklahoma Press, 1977), pp. 78-110. See also Philip P. Wiener, Evolution and the Founders of Pragmatism (Cambridge: Harvard University Press, 1949); and James D. Miller, "Holmes, Peirce and Legal Pragmatism," Yale Law Journal 84 (1975): 1123-40. (Donald R. Koehn, our contributing editor for the "Illustrations" and "Toward a Logic Book, 1872-73," has contributed also to this introduction and to other parts of the present volume.)
The following fourteen corrections to the first printing have been incorporated in the second printing; the original readings are given in brackets.
Enlarged [Enlarge]
202 [203]
Began Logic Notebook . . . Nov. ’09 [Lowell Institute . . . 1 Dec.]
1866 Lowell Institute . . . 1 Dec. [Began Logic Notebook . . . Nov. ’09]
1869 First of ca. 300 . . . Dec ’08 [Promoted to Rank of Assistant in the Survey]
Promoted to Rank of Assistant in the Survey [Put in charge of pendulum experiments, beginning in Nov.]
Enlarged [Enlarge]
“I . . . wholesome.” [‘I . . . wholesome’.]
complex [incomplex]
three dots have been removed from the first figure and one dot each has been added to the first and second figure
universel [universelle]
page 481 [page 000]
Enlarged [Enlarge]
Review [Reviev]
Emendations for errata 21.9, 24.22–23, 38.31, 348.19, which represent Peirce’s errors, have been added on pages 581, 582, 583, and 603.
32 [34]
‘Any T [‘In T]
incorrectly [correctly]
non-occurrence [non-occurence]
it is found [it is a found]
Line-end hyphenation of a good twenty French words was done according to the American method instead of the French syllabic method
réversion [reversion]
MSS 179–184, 187–189 [MSS 186–189]
[Spectrometer report (data)]. [ [Pendulum Observations and Comparisons].]
Toward the end of Peirce’s 1873 essay “On the Theory of Errors of Observation” in W3: 136 l. 11, Peirce explains that the general result of many experiments he had made upon the time it took for a person to react to various signals confirmed “the facts already in our possession, and which are due to the researches of Hirsch, Daumbusch, and others.” That passage was subsequently quoted or paraphrased by Annibale Ferrero in his Esposizione del metodo dei minimi quadrati and in a short discussion by Francesco Crotti titled “Intorno ad una proprietà della media aritmetica.”
The mystery concerns Daumbusch’s identity. Extensive searches on that name did not yield any satisfactory result. It is well known that Swiss astronomer Adolf/Adolphe Hirsch (1830–1901) had done pioneering studies in the early 1860s on physiological time and reaction time. It appears that Matthäus Hipp’s invention of the chronoscope in the 1840s provoked much research in experimental psychology. Hirsch used it to measure the physiological time of astronomical observers at work. No one by the name of Daumbusch surfaces within Hirsch's circle of assistants and colleagues, nor in the related secondary literature. Hirsch’s work influenced many others, and Wundt in particular (whose Leipzig laboratory included a Hipp chronoscope).
In situations like this, the natural hypothesis is that Peirce misremembered and thus misrendered the name. There are two plausible possibilities.
First possibility (suggested by Jeoffrey Gaspard). Peirce may have had in mind Swiss physiologist Emil du Bois-Reymond (1818–1896), a colleague of Helmholtz and a frequent correspondent of Adolph Hirsch, and well known for his Researches on Animal Electricity (1848 and 1884).
Second possibility. It turns out that Hirsch’s work particularly influenced prominent Dutch physiologist and ophthalmologist Franciscus Cornelis Donders (1818–1889; see e.g. this website). That Peirce meant Donders is also likely. Peirce’s “others” plausibly included such figures as Hermann von Helmholtz, Ludwig Eduard Rudolf Schelske, and Donders’s doctoral student Johan Jacob de Jaager.
Sample of primary references: Emil du Bois-Reymond, “On the Time Required for the Transmission of Volition and Sensation through the Nerves,” Notices of the Proceedings at the Meetings of the Members of the Royal Institution of Great Britain 4 (1862–1866), pp. 574–593 (13 April 1866). Franciscus Cornelis Donders, “Over de Snelheid van Psychische Processen,” Onderzoekingen, gedaan in het Physiologisch Laboratorium der Utrechtsche Hoogeschool, Tweede Reeks 2 (1868–1869): 92–120; “Die Schnelligkeit psychischer Processe,” Archiv für Anatomie, Physiologie und wissenschaftliche Medizin (1868): 657–681; “La vitesse des actes psychiques,” Archives néerlandaises des sciences exactes et naturelles 3 (1868): 296–317. Adolphe Hirsch, “Expériences chronoscopiques sur la vitesse des différentes sensations et de la transmission nerveuse,” Bulletin de la Société des Sciences Naturelles de Neuchâtel 6:1 (1862): 100–114. Ludwig Eduard Rudolf Schelske, “Neue Messungen der Fortpflanzungsgeschwindigkeit des Reizes in den menschlichen Nerven,” Archiv für Anatomie, Physiologie und wissenschaftliche Medizin (1862): 151–173.
Sample of secondary references: Serge Nicolas, “On the Speed of Different Senses and Nerve Transmission by Hirsch,” Psychological Research 59 (1997): 261–268 (translator’s historical introduction, 261–264; translation of Hirsch’s paper referenced above, 264–268). Jimena Canales, “Exit the Frog, Enter the Human: Physiology and Experimental Psychology in Nineteenth-Century Astronomy,” The British Journal for the History of Science 34.2 (June 2001): 173–197. Henning Schmidgen, “Time and Noise: The Stable Surroundings of Reaction Experiments, 1860–1890,” Studies in History and Philosophy of Science Part C: Studies in History and Philosophy of Biological and Biomedical Sciences 34.2 (June 2003): 237–275. Henning Schmidgen, “The Donders Machine: Matter, Signs, and Time in a Physiological Experiment, ca. 1865,” Configurations 13 (2005): 211–256 (© 2007). Geoffrey O’Shea and Theodore R. Bashore, Jr., “The Vital Role of The American Journal of Psychology in the Early and Continuing History of Mental Chronometry,” The American Journal of Psychology 125.4 (Winter 2012): 435–448.
“What really distinguishes intelligent action is that it is directed towards ends (as all vital action is) and varies as the ends vary, with a facility that does not belong to other vital processes.”
Volume 4 of this edition, published in 1989, the sesquicentennial year of Peirce’s birth, covers the years of his tenure as part-time lecturer in logic at the Johns Hopkins University, his only period of regular academic employment. At the same time Peirce continued his employment with the U. S. Coast and Geodetic Survey, made two further trips to Europe on official Survey business, and wrote or published some of his most important scientific papers. Consequently, this volume contains a multitude of research reports, research papers, and research notes in multiple fields, occasioned by fieldwork, instrumental work, metrological work, mathematical and logical investigations, class preparations, pedagogical reflections, academic meetings, and professional conferences. Many of the writings in this volume focus on logic and mathematics. The volume is therefore the direct reflection of years of intense activity and fertile creativity, much of it collaborative, in several disciplines.
Volume 4 includes extensive selections from Peirce’s classic 1879 report on gravity at initial stations, his studies on comparing a wave-length with a meter, and his renowned quincuncial projection of the sphere—a projection that has recently generated much renewed interest in different fields.
Among the significant logical and mathematical studies are “On the Algebra of Logic” (1880); “A Theory of Probable Inference” (1883) with the two “Notes” A and B following it in the celebrated collection of papers Peirce and his Johns Hopkins students authored under the title Studies in Logic; Peirce’s notes and addenda to Linear Associative Algebra by his father, Benjamin Peirce; and a number of papers never before published on thinking as cerebration, on the logic of relatives, on Boolian algebra and other algebras, on types of propositions, on junctures and fractures, and on the axioms and the logic of number. The penultimate essay, out of eighty, in volume 4, the metaphysical lecture on “Design and Chance,” introduces topics that would engage Peirce for the next several years, culminating in “A Guess at the Riddle” (1887–1888) and the cosmological articles published in The Monist in the early 1890s.
“If I am asked whether the study of logic really makes a man reason better, I am obliged to confess that in most cases it has the directly opposite result.”
| Preface | xi |
| Acknowledgments | xv |
| Chronology | xvii |
| Introduction | xix |
1. Read's Theory of Logic |
1 |
| 2. Spectroscopic Studies | 4 |
| 3. [Lecture on Logic and Philosophy] | 7 |
| 4. Note on the Progress of Experiments for comparing a Wave-length with a Metre | 10 |
| 5. On a method of swinging Pendulums for the determination of Gravity, proposed by M. Faye | 12 |
| 6. On the Algebraic Principles of Formal Logic | 21 |
| 7. Logic. Chapter I. Of Thinking as Cerebration | 38 |
| 8. Logic. Chapter I. Thinking as Cerebration | 45 |
| 9. Rood's Chromatics | 47 |
| 10. On the Ghosts in Rutherfurd's Diffraction-Spectra | 50 |
| 11. A Quincuncial Projection of the Sphere | 68 |
| 12. Note on the Theory of the Economy of Research | 72 |
| 13. Measurements of Gravity at Initial Stations in America and Europe | 79 |
| 14. A large number of repetitions of similar trials | 145 |
| 15. On the Vale of Gravity at Paris | 148 |
| 16. [On the State of Science in America] | 152 |
| 17. Letter, Peirce to Herve Faye | 157 |
| 18. On the Colours of Double Stars | 161 |
| 19. On the Algebra of Logic | 163 |
| 20. Chapter IV. The Logic of Plural Relatives | 210 |
| 21. Results of Pendulum Experiments | 212 |
| 22. [The Logic Notebook] | 214 |
| 23. [A Boolian Algebra with One Constant] | 218 |
| 24. The Axioms of Number | 222 |
| 25. [On Associative Algebras] | 225 |
| 26. Notes on Associative Multiple Algebra | 228 |
| 27. [Unequivocal Division of Finites] | 233 |
| 28. [Jevons's Studies in Deductive Logic] | 238 |
| 29. Width of Mr. Rutherfurd's Rulings | 240 |
| 30. Logic; and the Methods of Science | 241 |
| 31. Methods of Reasoning | 245 |
| 32. Note on the Mouse-Trap Problem | 257 |
| 33. Note on 0 degree | 258 |
| 34. [On Propositions and Syllogisms of Differing Order] | 260 |
| 35. Note on the Boolian Algebra | 264 |
| 36. Proof of the Fundamental Proposition of Arithmetic | 267 |
| 37. Comparison of the Metre with a Wave-Length of Light | 269 |
| 38. On the Logic of Number | 299 |
[NOTES AND ADDENDA TO LINEAR ASSOCIATIVE ALGEBRA] |
|
| 39. [Note on the Algebra g4] | 312 |
| 40. [Note on the Class of Algebras 2423] | 313 |
| 41. On the Relative Forms of the Algebras | 319 |
| 42. On the Algebras in which Division Is Unambiguous | 322 |
| 43. Brief Description of the Algebra of Relatives | 328 |
| 44. On the Relative Forms of Quaternions | 334 |
| 45. [On the Logic of Relatives] | 336 |
| 46. [On Relative Terms] | 342 |
| 47. Remarks on [B. I. Gilman's "On Propositions and the Syllogism"] | 345 |
REPORT OF A CONFERENCE ON GRAVITY DETERMINATIONS, HELD AT WASHINGTON, D.C., IN MAY, 1882 |
|
| [Edited by Charles S. Peirce] | |
| 48. [Introduction] | 350 |
| 49. Letter from Professor Hilgard to Major Herschel | 351 |
| 50. Reply of Major Herschel | 352 |
| 51. Six Reasons for the Prosecution of Pendulum | 356 |
EXPERIMENTS |
|
| 52. Notes on Determinations of Gravity, by C. A. Schott | 360 |
| 53. General Remarks upon Gravity Determinations, by John Herschel | 365 |
| 54. Opinions concerning the conduct of Gravity Work | 369 |
| 55. Resolutions | 377 |
| 56. Introductory Lecture on the Study of Logic | 378 |
| 57. On a Class of Multiple Algebras | 385 |
| 58. On Irregularities in the Amplitude of Oscuillation of Pendulums | 389 |
| 59. [On Junctures and Fractures in Logic] | 391 |
| 60. Letter, Peirce to O. H. Mitchell | 394 |
| 61. [Beginnings of a Logic Book] | 400 |
| 62. [On Propositions] | 402 |
STUDIES IN LOGIC |
|
| 63. Preface | 406 |
| 64. A theory of Probable Inference | 408 |
| 65. Note A: On A Limited Universe of Marks | 450 |
| 66. Note B: The Logic of Relatives | 453 |
| 67. A Communication from Mr. Peirce | 467 |
| 68. A Problem relating to the Construction of a reversible pendulum | 473 |
| 69. [Syllabus of Sixty Lectures on Logic] | 476 |
| 70. [Lecture on Propositions] | 490 |
| 71. [Lecture on Types of Propositions] | 493 |
| 72. [From a Lecture on the Logic of Relatives] | 501 |
| 73. [Introductory Lecture on Logic] | 507 |
| 74. A new Rule for Division in Arithmetic | 511 |
| 75. On the flexure of Pendulum Supports | 515 |
| 76. On the Deduction of the Ellipticity of the Earth from Pendulum Experiments | 529 |
| 77. On a Method of Observing the Coincidence of Vibration of Two Pendulums | 535 |
| 78. Additional Note on the Method of Coincidences | 541 |
| 79. [Design and Chance] | 544 |
| 80. [On the Teaching of Mathematics] | 555 |
| Notes | 559 |
| Bibliography of Peirce’s References | 595 |
| Chronological List, 1879-1884 | 603 |
| Essay on Editorial Method | 615 |
| Symbols | 632 |
| Textual Apparatus | 634 |
| Headnotes, Textual Notes Emendations | |
| Line-End Hyphenation | |
| Rejected Substantive Variants | |
| Line-End Hyphenation in the Edition Text | 684 |
| Index | 685 |
The years 1879-84 were perhaps the most fulfilling and disappointing in the life of Charles Sanders Peirce. He saw the promise of a long hoped for academic career, established important academic contacts and had remarkable successes as a teacher, and gained international prominence as a scientist. But in 1884 his academic career ended in disgrace, and his scientific reputation was soon to suffer a serious assault. His purpose and sense of direction would be so battered that he would retreat to the seclusion of a country house to spend the rest of his life with his second wife, Juliette. However, during these years, amid the turmoil of personal victories and private calamities, Peirce worked at a fever pitch and produced some of his most important writings. 1
The most momentous and consequential event during these years was the death of his father on 6 October 1880. Born in 1809, Benjamin Peirce was Harvard's Perkins Professor of Astronomy and Mathematics for nearly 40 years, and America's leading mathematician. He was largely responsible for introducing mathematics as a subject for research in American institutions, and he is known especially for his contributions to analytic mechanics and linear associative algebra. He helped organize the Smithsonian Institution, and from 1867 to 1874 served as superintendent of the United States Coast Survey. Benjamin Peirce was generally regarded as the most powerful mind so far produced in the United States. 2
At the time of Benjamin's death, it was thought that of his four surviving children (Benjamin Mills had died in 1870) the one most endowed with his intellectual powers was Charles, who was expected to carry on his father's work. Benjamin himself appears to have expected as much, for at the close of his remarks on the impossible in mathematics before the Boston Radical Club near the end of his life, he "observed that his son Charles was now engaged in carrying on his investigations in the same line to which he had specially applied himself; and it was a great gratification to him to know that his son would prosecute the work to which he had devoted the latter part of his own life." 3
There is no doubt that his father had greater influence on Charles's intellectual development than did anyone else. Early on he had recognized his son's powers and had taken a regular and ongoing interest in his education and career. He got Charles started with the Coast Survey, giving him a salaried position in 1867, and put him in charge of pendulum operations, and in so doing, set the course for Charles's scientific work for the remainder of his career with the Survey. When in 1870 they traveled home to Cambridge from Michigan with the body of Benjamin Mills, he advised Charles against trying to make a career of logic; it would be better, he said, to stick with science. When his father died in 1880, Charles may well have remembered this advice, for he soon announced that he would quit logic and philosophy.
The full impact on Charles of his father's final illness and death can only be guessed at. The emotional toll is manifested in his impulsive decision to quit logic and philosophy and sell his library, a decision he soon came to regret, and in a general malaise that settled over him. Upon returning to Baltimore after the funeral in Cambridge, Peirce wrote to his mother in late October: "I have had a fog resting on my spirit ever since I have been back, so that I have not been working very successfully but I hope it is clearing up. It has been just like a steamer forging through a fog." That image may well have been vivid for Peirce. Because of his father's grave condition a few months earlier, in late July, he had been called home from Europe where he had been on assignment for the Coast Survey, and it is likely that he returned aboard the French steamer St. Laurent which arrived in New York on 4 August "after a passage in which it had strong W. gales and fog most of the time." 4
The effect of his father's death on the direction of
Peirce’s work was immediate. Along with his brother, James Mills,
Charles turned to Benjamin's writings, hoping to get more of them into
print. He spent much of the next year editing and annotating his
father's privately printed Linear Associative Algebra of 1870.
Mathematical topics began to occupy him more frequently than ever
before, although this was also due to the influence of the mathematical
community in which he found himself at the Johns Hopkins University. But
Peirce was already a talented mathematician who had accomplished enough
to be included in the small group of scientific men in America who were
capable of contributing to sciences that were laden with mathematical
theory. Other men in this group, mainly mathematical astronomers,
included Simon Newcomb, Asaph Hall, and George William Hill.
Probably the greatest effect of Benjamin's death on Charles was the loss of the influence and protection that his father's reputation had provided. Benjamin had been so highly regarded in scientific and academic circles, and his opinions and interests had carried such weight, that Charles almost always received special consideration. After his father's death this protective influence ended and Charles was left to make his own way.
The loss of his father was soon followed by the death of Carlile P. Patterson, who in 1874 had succeeded Benjamin Peirce as superintendent of the Coast Survey. Patterson's death on 15 August 1881 brought to an end the golden age of the Coast Survey, a time when pure research was much esteemed and the daily course of activity was governed by a desire to learn and discover as much as by the need to achieve practical results for a technologically oriented and sometimes shortsighted Congress. Patterson had been an ideal employer and it appears from Peirce’s eulogy (P 264) that he feared a change for the worse:
"His superintendency was marked by . . . great practical achievements. . . . Yet, although he was not professedly a scientific man, under none of the eminent geodesists who had preceded him was more stress laid upon the scientific branches of the work—to their extension, and to the precision of their execution.
"No one was so earnest as he to secure to the Survey the labors of men of purely scientific, and especially mathematical, attainments and abilities.
". . . I feel that in Patterson's death the science of the country has lost a staunch ally."
As it turned out, Peirce had good reason to fear the worst. No sooner had Julius Hilgard taken over as superintendent, something Benjamin had sought to prevent, than Peirce was put on notice that his reports would have to be more timely. In this way Hilgard let it be known that he did not have Patterson's patience for Peirce’s exacting and time-consuming methods nor, perhaps, for delays caused by his recent commitment to the Johns Hopkins. So began a period of disaffection that in 1891, after thirty-one years of service, led to Peirce’s forced resignation. In the meantime Hilgard had led the Survey into a public scandal and, after his dismissal in 1885, the Survey fell for the first time into the hands of F. M. Thorn, a bureaucrat with no training in science.
Nearly as consequential for Peirce as his father's death was his divorce from his first wife, Harriet Melusina (Zina) Fay Peirce, on 24 April 1883, and his marriage to Juliette Annette Froissy Pourtalai (or de Pourtalès) just six days later. Peirce and Zina had married on 16 October 1862 and they lived together until Zina refused to accompany Peirce when he moved from Cambridge in October 1876. Although her reasons have never been fully disclosed, it is clear that Zina was unwilling to live the itinerant life that Peirce thought essential for his work with the Survey. She never remarried and in later years expressed regret that she had not stayed with Peirce.
Sometime during his separation from Zina, perhaps within the first year, Peirce met Juliette, who was thought to be the widow of a Count Pourtalai and the sister of a diplomat brother who had, it seems, been known to George Bancroft while he was ambassador to Prussia. Bancroft is said to have recognized Juliette in America from her resemblance to her brother. She was generally thought to be a Frenchwoman, but she actively suppressed all accounts of her origin and her identity remains uncertain.
Peirce probably met her
at the Brevoort House, a European-styled hotel located on Fifth Avenue
near Washington Square, where he usually stayed when in New York City.
He was well known to the manager of the Brevoort, who reportedly
introduced Peirce and Juliette on the occasion of a great ball.
Of those outside Baltimore who knew of Peirce during the period covered by the present volume, most thought of him as a scientist in the service of the Coast Survey. 7 His association with the Survey began in 1859 and in July 1861 he was appointed a regular aide. In 1867, less than five months after Benjamin had become superintendent, Charles was promoted to a salaried position and began his rise to prominence in science. His primary field of scientific endeavor became geodesy, a field he led after 1872 when his father promoted him to assistant, the rank immediately below that of superintendent, and put him in charge of pendulum experiments. The two main aims of Peirce’s geodetic operations were to determine the force of gravity at various locations in the United States and abroad and, from these results, determine the figure of the earth.
But Peirce’s scientific work extended far beyond geodetic operations. He made notable contributions to metrology, for example. Precise determinations of gravity require exact measurements of the length of the pendulums employed, and exact measurements demand that precise relations to standards of length be determined. Consequently, Peirce spent a good deal of time comparing the lengths of Coast Survey pendulums with recognized standards of length throughout Europe, and with each other, under controlled conditions. This work led to a more generalized interest in standards, and for several months in 1884-85 he was in charge of the U.S. Office of Weights and Measures.
It seems natural that extensive work with pendulums should have led an inquiring mind like Peirce’s to reflect on the methodology of pendulum experimentation and on the adequacy of the instruments themselves. To some extent such reflection was part of the job, for it was essential that the data of observations be "corrected" to eliminate the effect of systematic sources of error. Peirce was adept at this work and in addition to establishing that the flexure of the stand of a popular pendulum (the Repsold compound pendulum) was an important source of error, which demonstrated the need for corrections to many of the gravity determinations of leading European scientists, Peirce conducted numerous experiments to determine additional sources of error. These included the effect of the wearing of the knife-edge (the thin blade on which the compound pendulum oscillates), the effect of using steel cylinders instead of knives, the effect of the oscillation of the walls of the receiver (the container in which the pendulum swings), and the effect of temperature on the length of the pendulum. Peirce also invented two styles of pendulum (only one of which was constructed) as well as a new kind of pendulum stand.
At the beginning of the period 1879-84 Peirce was involved with the U.S. Treasury Department in a matter that may have planted seeds of disaffection with the Survey. Late in 1878 he had requested an increase in his salary, from $2870 to $3500 and was so determined to have his raise that he was prepared to submit his resignation should it be refused. "I prefer working for somebody who will consider the character of my work," he wrote to his father on 14 January 1879. (Peirce may have had Daniel C. Gilman in mind, the president of the Johns Hopkins University, with whom he had been in correspondence for more than a year about the possibility of an academic appointment.) By 8 July Superintendent Patterson sent the request to John Sherman, Secretary of the Treasury, with the following supporting argument:
"Mr. Peirce is forty years of age, has been employed on the Survey for eighteen years, and on account of his exceptional ability for special investigations, was during eleven years service rapidly advanced to his present pay in 1873. Since that date Mr. Peirce has made extraordinary advances in Pendulum observations of a very original character, exciting the deepest interest in this important scientific subject on the part of all physicists, both in this country and abroad, and leading to a complete revision of all past observations at the main initial points for Pendulum observations in Europe. In fact Mr. Peirce is the first person in this country who has with any success attacked this problem, the subject having remained in abeyance for many years, awaiting a truly scientific observer. Mr. Peirce has also succeeded in comparing the accepted standard unit of length (the meter) with a permanent (so far as now known) length in nature, a wave length of light, a task hitherto never attempted on account of the inherent difficulties of the case, over which after many discouragements and failures he has at last triumphed. These results of Mr. Peirce’s work have greatly advanced the science of Geodesy, the scientific reputation of the Survey, and therefore that of the Country.
"The enclosed extracts from letters of eminent American Scientists offer the best evidence of the value of Mr. Peirce’s work." 8
The eminent scientists were Alfred M. Mayer, professor of physics at Stevens Institute of Technology; Wolcott Gibbs, Rumford Professor at Harvard University; Ogden N. Rood, professor of physics at Columbia College; and Benjamin Peirce.
Mayer reported that the results of Peirce’s work already "are of the highest importance to the advancement of science and to the interest of the U.S. Coast Survey. Mr. Peirce’s methods are original, and of an accuracy and refinement which are unsurpassed"; he added that "Mr. Peirce deserves well of his countrymen, for his work has added much to the scientific reputation of the U.S. Coast Survey among European nations." Gibbs discussed the spectroscopic apparatus that Peirce used in his experiments with light waves. "I have carefully examined the apparatus," he said, "and am of opinion that it is admirable both in design and in workmanship. In fact I do not hesitate to say that both the spectroscope and spectrometer are the most perfect instruments of the kind in existence, and I have been both delighted and instructed by a critical examination of the refinements introduced in their construction." Rood addressed Peirce’s general merit and the "very high estimation in which Mr. Peirce’s contributions are held by the scientific men of this country and of Europe," and he claimed that "it would be difficult to find another scientist having similar qualifications with Mr. Peirce either in the special education required, or in natural ability. I certainly know of no one in this country who would be at all qualified to take the position which he now holds in your Survey." Finally, Benjamin Peirce, whose relation to Charles may have somewhat diluted the impact of his remarks, wrote of his son's work in establishing a wave-length of light as a standard of length:
"It is a most remarkable achievement to have thus determined the length of the meter from the wave-length of light, which is the shortest length which has ever been measured; and the only sure determination of the meter, by which it could be recovered if it were lost to science. It will certainly secure for the Survey the applause of all scientific men.
"When combined with Mr. Peirce’s admirable measures of the pendulum, which have justly been regarded by the savans of Europe as adding a new era to this most difficult branch of observation, it places him among the great masters of astronomical and geodetic research, and it would be most unfortunate, i[f] such grand strides in science were not suitably acknowledged."
But Peirce did not get his raise. In his letter conveying Sherman's decision, Patterson regretfully assured Peirce that he would do anything in his power to advance his interests outside the Survey, but said that it would be difficult to replace him. By the time Peirce heard of Sherman's denial he had received his part-time appointment at the Johns Hopkins and he concluded that with his combined salaries he was sufficiently well off. Besides, he felt that Patterson, who had admitted that he was not adequately paid, might be "more or less indulgent" of his connection with the Johns Hopkins—a recognition of the potential difficulty of pursuing two careers at once.
William James had recommended Peirce to Gilman for the professorship of logic and mental science in 1875, and Benjamin Peirce had later recommended him for the professorship of physics. By 13 January 1878 Peirce had informed Gilman of his strong interest in being "called" to the Johns Hopkins and had set out in detail his projected program for the physics department. Peirce emphasized that he was a logician and had learned physics as part of his study of logic; for "the data for the generalizations of logic are the special methods of the different sciences. To penetrate these methods the logician has to study various sciences rather profoundly." He then described his view of logic and remarked on the importance of his work:
"In Logic, I am the exponent of a particular tendency, that of physical sciences. I make the pretension to being the most thorough going and fundamental representative of that element who has yet appeared. I believe that my system of logic (which is a philosophical method to which mathematical algebra only affords aid in a particular part of it) must stand, or else the whole spirit of the physical sciences must be revolutionized. If this is to happen, it cannot be brought about in any way so quickly as by the philosophical formularization of it and the carrying of it to its furthest logical consequences. If on the other hand it is to abide, its general statement will be of consequence for mankind. I have measured my powers against those of other men; I know what they are. It is my part to announce with modest confidence what I can do. My system has been sketched out but not so that its bearings can be appreciated. If the world thinks it worth developing, they have only to give me the means of doing it. But if not, I shall follow another path, with perfect contentment."
Gilman inquired on 23 January whether Peirce would accept a half-time appointment as lecturer of logic, while retaining his position with the Survey. Peirce replied on 12 March that he would.
"The truth is that the great difficulty I had in reaching a decision was that if I were to be your professor of logic, my whole energy and being would be absorbed in that occupation. Right reasoning is in my opinion the next thing in practical importance to right feeling; and the man who has to teach it to young minds has such a tremendous responsibility, that the idea of giving 1/2 his activity to such a business seems shocking. All the more so, that students have hitherto been fed with such wretched bran under the name of logic. That name now rests under a just opprobrium from which, if I should become your professor, it would be the purpose of my life to redeem it, first in the eyes of those who had been my pupils, and next before the world; for I should think that I had failed if my pupils did not carry into after-life a more distinct idea of what they had learned from me than of most of the subjects of their study and did not feel that the study of reasoning had been of great advantage to them."
But the trustees had already decided not to make any further appointments that year.
Gilman inquired again the following year, and though Peirce now set certain conditions, he again replied affirmatively (on 6 June 1879). He wanted to have sole charge of instruction in logic and the assurance that the position would eventually be full-time. Furthermore, he advised Gilman that he would be on Coast Survey business in Europe until after the beginning of the fall term. As for the teaching of logic, Peirce’s views were much the same as he had expressed the previous year.
"There are two things to be done; one, to communicate the logica utens, and to make expert reasoners of the pupils, able to form clear ideas, to avoid fallacies & to see in what quarters to look for evidence; the other, to familiarize them with the logical ideas which have percolated through all our language & common sense, & to show their significance & what they are worth. Special branches of logic may of course be taught in special cases; such as logical algebra, the history of logic, etc. etc."
On 13 June 1879 Gilman made an offer which Peirce accepted on 20 June, the day after he received it.
So it happened that for most of the period 1879-84 Peirce pursued two careers: as a scientist in the most prestigious scientific agency in America and as a teacher and scholar in the most advanced American school for graduate studies. Peirce was a regular commuter on the B & O railroad between Washington and Baltimore during these years. He tried to do well in both jobs, but that was a formidable predicament and, as it turned out, a near impossibility. Given the demands of his position of leadership in the Coast Survey, which included frequent travel and sustained periods of research and experimentation, and the pressures of a new career in teaching with the excitement of his longed-for interaction with brilliant students, it is not surprising that Peirce’s health began to break. He struck an alarming note toward the end of his first term of teaching when in a curious letter to Gilman, written on Christmas Day 1879, he wrote:
"I have an odd thing to say to you which is to be perfectly confidential unless something unexpected should occur. In consequence of certain symptoms, I yesterday went to see my physician in New York, & he after calling in an eminent practitioner in consultation, informed me that he considered the state of my brain rather alarming. Not that he particularly feared regular insanity, but he did fear something of that sort; and he must insist on my being some little time in New York and he could not promise that I should go back on January 5th. For my own part, I do not think the matter so serious as he thinks. The intense interest I have had in the University and in my lectures, combined with my solitary life there, & with the state of my physical health, has undoubtedly thrown me into a state of dangerous cerebral activity & excitement. But I feel convinced that I shall surprise the doctors with the rapidity with which I regain my balance. I don't think the matter of any particular importance. However, I think it best to say to you as much as I do say; both that you may understand why I may possibly not be on hand Jan 5, and also because the matter might turn out worse than I anticipate, and I might do some absurd thing. I have said nothing to anybody else than you; & I beg you will not let me see that it is in your mind when I go back; for I shall not go back until it is quite over."
The matter was apparently no more serious than Peirce had thought, but it is true that for the next several years he suffered from ill health.
It is amid the events and circumstances so far described that Peirce’s writings of this period were created. Although much of his work exhibits his dual preoccupations—his scientific work is reflected in his academic work, and vice versa—his writings generally concern one or the other of his pursuits. These pursuits are distinct enough to be treated separately, though it is well to keep in mind the parallel unfolding of the events described in the following two sections.
The Coast and Geodetic Survey
Although the decade preceding 1879-84 has sometimes been regarded as Peirce’s most "intensely scientific period," he seems to have lost little intensity during the present period. A review of his scientific undertakings and accomplishments reveals that his productivity remained on a par with that of the previous decade. However, his reliability, especially with regard to the preparation of his field reports, did decline somewhat. With his part-time employment at the Johns Hopkins Peirce could not be so single-mindedly directed toward scientific undertakings as he had been during the 1870s. But Peirce’s commitment to teaching did not keep him from carrying on a full life of science.
From 1879 to 1884 Peirce was in charge of half a dozen major pendulum observation parties at several sites in Pennsylvania and at St. Augustine, Savannah, Fortress Monroe in Virginia, and the Smithsonian. Extensive experiments were also conducted in Baltimore and Cambridge and at the Stevens Institute in Hoboken, New Jersey. Besides these domestic occupations Peirce led an observation party to Montreal in 1882, and in the summers of 1880 and 1883 he made the final two of his five sojourns to Europe on assignment for the Coast Survey. The fieldwork for these assignments resulted in one to two hundred field books of experimental data, and it generated over a linear foot of detailed correspondence (most of which is deposited in Record Group 23 in the National Archives). In addition to these major assignments Peirce performed the regular functions of his office and he carried out a number of other experiments at the Washington headquarters. He conducted experiments with his spectrum meter in his attempt to establish a wave of sodium light as a unit of length and he oversaw the construction of four pendulums of his own design (Peirce Pendulums 1 - 4). Throughout these years Peirce was always at work on the reduction of the data of his field notes and on the preparation of reports for publication, primarily for the superintendent's annual reports. He saw more than a dozen scientific papers into print and he contributed at least as many papers and reports to scientific associations, most notably the National Academy of Sciences.
In 1879 Peirce’s initial concern was to get fieldwork
underway in accordance with his assignment to determine the disturbing
effect of the Appalachian mountains on geodetic operations. Early in
January he occupied the Allegheny Observatory in Pennsylvania
Peirce’s fieldwork was completed at Allegheny in March and resumed at Cresson in July and at Ebensburgh in mid-August. Field operations at these Pennsylvania stations were concerned with the determination of gravity but also with sources of error resulting from the nature of the pendulum apparatus itself. Peirce had worked on the latter since 1875 when he had surprised Europe's leading geodesists at a Paris conference where he proclaimed that the stand of the Repsold pendulum was unstable and thus a systematic source of error.
Peirce had acquired a Repsold pendulum during his second European assignment in 1875, and had made a series of determinations at selected European locations (or "initial stations") in order to relate American to European results. In his report on these determinations he emphasized that "The value of gravity-determinations depends upon their being bound together, each with all the others which have been made anywhere upon the earth." He had made determinations in Berlin, Geneva, Paris, and Kew, and had met such leading figures as James Clark Maxwell of Cambridge, Johann Jakob Baeyer of Berlin, and Emile Plantamour of Geneva.
It appears that General Baeyer had first raised the suspicion that the Repsold stand might be unstable. Peirce examined the stand in Geneva and worked out an approximate value of the error due to its swaying, which he presented at the Paris conference. If Peirce was right, all of the results published in Europe during the previous ten years would be vitiated. Although Peirce’s claim drew little response, Hervé Faye suggested that such an error might be overcome by setting up two pendulums on the same stand and by swinging them simultaneously in opposite directions. The following year at a meeting in Brussels, which Peirce did not attend, it was concluded that he was mistaken. Peirce resolved to defend his claim at the next meeting of the European Geodetic Association in 1877 in Stuttgart. With abundant experimental data in hand and with the mathematical theory well worked out, Peirce won the day. He later reported that "from that time I was acknowledged as the head of that small branch or twig of science." 10
The results of Peirce’s geodetic work in Europe, and some subsequent work in the United States, were set forth in the extensive monograph entitled "Measurements of Gravity at Initial Stations in America and Europe" (item 13), which is regarded as one of the classics of geodesy and the first notable American contribution to gravity research. It was specially noted at the Munich meetings of the International Geodetical Association in 1880 and it is listed as a basic monograph on the pendulum in the 1904 Encyklopädie der mathematischen Wissenschaften. The results of Peirce’s work on flexure were presented in April 1879 at a meeting of the National Academy of Sciences (P 152) and appeared not long after in the American Journal of Science and Arts as "On a method of swinging Pendulums for the determination of Gravity, proposed by M. Faye" (item 5), which shows the theoretical soundness of Faye's method for avoiding error due to flexure.
Three more papers that Peirce read to the Academy in April indicate his other scientific endeavors. His "Comparison of the meter with wave lengths" (P 154) detailed his efforts to establish wave-lengths of light as a standard of length, a different version of which (P 133) was presented by his father to the American Academy of Arts and Sciences in Boston. Although summary reports of this work were published in various scientific journals—as in items 2 and 4, or in his "Mutual Attraction of Spectral Lines" in Nature (P 156)—no major study was ever published. By 1886 Peirce had several times revised his report on the spectrum meter but the finished monograph has been lost. Item 37 is what remains of an 1882 version.
In his spectrum meter experiments, Peirce compared wave-lengths of light with the breadth of a diffraction plate. He used a machine called a comparator, a spectrometer he himself designed, and a diffraction plate designed by Lewis M. Rutherfurd. These experiments led him to the discovery of hitherto unknown diffraction phenomena called "ghosts," which provided the topic for his third paper to the National Academy (P 153) and the published paper "On the Ghosts in Rutherfurd's Diffraction-Spectra" (item 10).
Peirce’s fourth paper, "On the projections of the sphere which preserve the angles" (P 151), was the first public presentation of his quincuncial projection; it was later published in the American Journal of Mathematics (item 11) and in the 1876 Coast Survey Report (P 138; see also P 238). The quincuncial projection allowed for repetition of the whole sphere in transposed positions on the map so that any location might be viewed as occupying a central position relative to the rest of the earth. It was used during World War II for charting international air routes. Peirce had completed most of the work on the projection by 1879 and the first quincuncial map appeared in May 1879 in an appendix to the Proceedings of the American Metrological Society, but there it was only a convenient map for showing the date-line from pole to pole, not a new projection with supporting mathematical theory.
Another classic paper in the 1876 Report (in addition to item 13) is Peirce’s "Note on the Theory of the Economy of Research" (item 12). The theory developed in this paper was intended to guide scientific researchers in their efforts to balance the benefit of advancing knowledge against the costs of the research. The main problem of the doctrine of economy is "how, with a given expenditure of money, time, and energy, to obtain the most valuable addition to our knowledge," a problem that concerned Peirce even in his later years. This paper has been reprinted as recently as 1967 in Operations Research.
Two other papers published in 1879 illustrate the scope of Peirce’s scientific interests during the period 1879-84. The 16 October issue of the Nation contained his review of Ogden Rood's Modern Chromatics (item 9), which makes several references to Peirce’s own experimental work on color, and the 1876 Coast Survey Report contained yet a third paper, entitled "A Catalogue of Stars for observation of latitude" (P 159). This catalogue, which was intended to supersede the list published in the 1873 Report (P 95), does not appear under Peirce’s name, but J. E. Hilgard's preface indicates that "the list was selected under the direction of Assistant C. S. Peirce, and the names of the stars were assigned by him."
Peirce concluded his fieldwork for the determination of the disturbing effects of the Allegheny mountains with a three-month occupation of a station at York, Pennsylvania, in 1880. Henry Farquhar conducted the operations, which continued until mid-June, under Peirce’s direction. In addition to measurements of gravity, observations were made for the detection of flexure and experiments were conducted in which the standard pendulum knife was replaced by small steel cylinders that acted as bearings. This method had been proposed by both Peirce and Yvon Villarceau in order to avoid the effects of the blunting of the knife-edge, but Peirce eventually showed that the cylinders increased rather than reduced friction.
Peirce sailed on his fourth Coast Survey assignment to Europe in April. Although his previous gravity determinations in Paris varied significantly from the accepted measures of Borda and Biot, he demonstrated that, when corrected for errors not suspected at the time of their observations, their work came into line with his. His paper "On the Value of Gravity at Paris" (item 15) is a translation of the paper he presented to the French Academy of Science and published in the Academy's Comptes Rendus (P 171). Peirce intended to report on his pendulum work and his spectrum meter at the International Geodetic Association meeting in September in Munich but, as mentioned earlier, he was called home when his father became seriously ill. He sent an abbreviated report in the form of a letter to Hervé Faye, which was published in the Association's proceedings (item 17).
After his return from Europe in 1880, for his father's final illness and death, Peirce does not appear to have taken up any new projects right away. He provisionally completed his comparison of the meter with a wave-length (although he soon resumed that study), pursued his investigations of the effect of the walls of the receiver on the period of oscillation, and labored to improve the related mathematical theory. In mid-November he read a paper "On the ellipticity of the earth as deduced from pendulum experiments" to the National Academy of Sciences in New York City; it was later published in the 1881 Coast Survey Report (item 76).
Several more of Peirce’s scientific writings appeared in print in 1880. In July, Nature published "On the Colours of Double Stars" (item 18), and "The quincuncial projection" was reprinted in the 1876 Coast Survey Report. A summary of the "Measurements of Gravity at Initial Stations" appeared as "Results of Pendulum Experiments" in the October issue of the American Journal of Science and Arts (item 21, which was reprinted in the November issue of The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science), and a report of his pendulum operations was included in the 1879 report of the Commission der Europæischen Gradmessung (P 184).
Much of Peirce’s Coast Survey work during the first half of 1881 focused on the construction of his four invariable reversible pendulums which, according to Hilgard, had their surfaces "as nearly as convenient in the form of an elongated ellipsoid." Peirce had invented the pendulums so that the effects of viscosity could be theoretically ascertained. Three of them (Nos. 1, 2, and 4) were meter pendulums, and one (No. 3) was a yard pendulum. Peirce No. 1 was used in the Arctic, in Franklin Bay above the 80th Parallel, by an expeditionary party led by Lieutenant Adolphus W. Greely later in the year. Greely's party was one of two U.S. parties assembled as a result of a meeting in Hamburg in 1879 where eleven nations 11 had agreed to man polar stations for one year (1882-83) to conduct scientific observations and pool their results. Included in Greely's assignment was pendulum work for the determination of gravity, which Peirce had carefully planned. He had personally instructed Greely's astronomer, Sergeant Edward Israel, in the conduct of the experiments. Unhappily, Greely's party suffered terrible hardships and eighteen of his twenty-five men died during the course of the next three years, including Israel. Although he and Greely had meticulously recorded and maintained the records of their pendulum experiments, Peirce at first concluded from the data that some accident must have befallen the pendulum. When he recorded this opinion in his official report of the experiments (P 369), it occasioned a mild dispute. But it ended amicably when Peirce assured Greely that "there has been no failure, but this determination is far more reliable than any other which has ever been made within the arctic circle, and this will be take my assurance of it the ultimate judgment of experts".12
In mid-April 1881, Peirce delivered a report "On the progress of pendulum work" to the National Academy of Sciences (P 199), and in June he made gravity determinations at Washington, in late July and August at Baltimore, and in September at Cambridge. He continued his investigations of error due to the flexure of the stand and the receiver and he experimented with the Faye/Peirce plan of swinging two pendulums from the same support. In July he sent his letter to Faye (item 17) and saw the publication of his "Width of Mr. Rutherfurd's Rulings" in Nature (item 29), and in August he attended the thirtieth meeting of the American Association for the Advancement of Science in Cincinnati where he read a paper entitled "Comparison Between the Yard and Metre by Means of the Reversible Pendulum" (P 186). On 30 August he was elected to membership in the Association and was appointed to the standing committee on weights and measures.
Although Peirce’s reputation as a geodesist was strong as 1882 got underway, he was beginning to be a source of irritation inside the Survey, primarily because of his growing tendency toward tardiness in reducing the results of his fieldwork and the preparation of reports for publication. In April he was urged by Richard D. Cutts, assistant in charge of the Survey office, to send in his appendices for the 1881 Report and, on 6 July, Superintendent Hilgard informed him that it had gone to press without the four appendices ("Determination of Force of Gravity at points in Penn.," "Variation of Gravity with the Latitude," "Flexure of Pendulum Supports," and "Oscillation Period of the Walls of the Receiver"). He implored Peirce to concentrate on what could be finished by 20 July, the final day for submission, and to let him know at once which papers could not be finished so that reference to them might be struck from the report. Surprisingly, the 1881 Report appeared with four appendices by Peirce, although the first of the four listed above was not included. Because of its bulkiness it was also absent from the 1882 Report, but it finally appeared as Appendix 19 in the 1883 Report (P 290).
In April 1882 Major John Herschel of the India Survey arrived in the United States to conduct gravity operations at selected stations in order to connect British with American pendulum work. Peirce helped him get set up at Hoboken and frequently assisted him during his year-long stay. In May Herschel was invited to participate in an informal conference on the future of pendulum work and the efficiency and accuracy of the methods employed, a conference no doubt occasioned by his presence in the United States and by his prominence in the field of pendulum operations. Those in attendance besides Peirce and Herschel were Simon Newcomb of the Nautical Almanac and Superintendent J. E. Hilgard, as well as George Davidson and C. A. Schott of the Coast Survey. J. W. Powell, director of the United States Geological Survey, was unable to attend. Peirce edited the proceedings of the conference, which were published in the 1882 Report (items 48-55).
In addition to the considerable attention he gave to Herschel's pendulum operations throughout the year and to his supervision of the construction of the Peirce pendulums (work on No. 4 was still underway in May), Peirce conducted extensive fieldwork of his own. From May through September he made gravity determinations and other pendulum observations in Washington, Baltimore, Hoboken, Montreal, and Albany. Although he continued to swing the Repsold pendulum in order to coordinate his operations with those of Herschel and others, he also made observations with his new invariable reversible pendulums. By the end of 1883, Peirce Pendulums 2 and 3 had been swung at Washington, Hoboken, Montreal, Albany, and St. Augustine.
Peirce traveled to Montreal in August to make a series of pendulum experiments at the McGill College Observatory and to attend the thirty-first meeting of the American Association for the Advancement of Science. The work was very demanding and beset with complications due to equipment problems. Peirce was beginning to feel the strain of overcommitment. On 29 August he wrote to his mother:
"For a long time I have been so driven with work that I have had no time to write the smallest line except in the way of business. . . . I have prepared an enormous quantity of matter for the press of late,—almost enough to make a volume of the Coast Survey Reports. . . . I have also been very active in the line of experiments, frequently working all night. Hilgard is a regular task-master. My assistants and I have been nearly killed with overwork."
Yet Peirce managed, somehow, to take in some of his surroundings. His letter continues: "I am charmed with Montreal. It is a most lovely site, much of the architecture is fine, there is very little that is utterly dreary, and the admixture of the French element contributes something very pleasing."
Peirce had not traveled to Montreal alone. Juliette had accompanied him on the train and may have stayed with him for a short time in Montreal before traveling with her maid to Quebec City. When Peirce left on 10 September after completing his work in Montreal, Juliette again accompanied him. They stopped over in Albany, where Peirce visited the Dudley Observatory, and they stayed at the same hotel. Peirce’s brazenness in his relations with Juliette, whether from innocence or arrogance, did not go unnoticed, especially by Superintendent Hilgard.
Operations at the Fort Marion station in St. Augustine were occasioned by a field party sent by the French government to observe the 6 December transit of Venus. Peirce was assigned to assist the French party by determining the longitude of the station, which he did with the assistance of E. D. Preston, at a station in Savannah, Georgia, and Captain Desforges at Fort Marion. Although he does not seem to have spent much time in Florida in December, he did oversee the setting-up of the station, and he wrote the 21 December letter to Mitchell with a graphical notation for the logic of relatives (item 60) from St. Augustine.
Peirce read four papers to the National Academy of Sciences in 1882, two based on his work at the Johns Hopkins and two on his work for the Survey. The practice of reading papers based on his work at the Johns Hopkins seems to have begun in November 1881 when he read a version of his "Logic of Number" (item 38). In April he presented "On a fallacy of induction" (P 233), which he had read five months earlier to the Johns Hopkins Scientific Association (P 211). At the November meetings, he presented "On the logic of relatives" (P 235), which was probably a version of his soon to be published "Note B" in Studies in Logic (item 66). He also read two papers resulting from his Coast Survey work, "On the determination of the figure of the earth by the variations of gravity" (P 234) and "On Ptolemy's catalogue of stars" (P 236). The first paper may have been a version of what he had read to the Johns Hopkins Scientific Association in 1881 (P 210) and had published in 1883 as "On the Deduction of the Ellipticity of the Earth from Pendulum Experiments" (item 76).
Three of Peirce’s scientific papers appeared in print in 1882. In October "On Irregularities in the Amplitude of Oscillation of Pendulums" was published in the American Journal of Science and Arts (item 58), which is a response to remarks made by O. T. Sherman in an earlier issue of the Journal (24:176). Volume 13 of the Annals of the Astronomical Observatory of Harvard College, entitled Micrometric Measurements and published in 1882, contains the results of extensive observations made under the direction of Joseph Winlock and Edward C. Pickering during the years 1866-81. Peirce was one of the principal observers during many of those years and much of his work is represented in the volume (P 219). The third publication (P 238) is in Thomas Craig's A Treatise on Projections, which contains an extract from the "Quincuncial Projection" first published in 1879 (item 11).
Peirce’s Coast Survey work for the first four months of 1883 consisted primarily of fieldwork at the Smithsonian and at Hoboken. In late December 1882 and continuing through most of January 1883 he was at the Smithsonian, and in February he reoccupied the Stevens Institute at Hoboken, where Peirce Pendulums 2 and 3 were swung for the purpose of comparing the yard with the meter. In March and April he was back at the Smithsonian.
April 1883 was an important month in Peirce’s personal life. Emotions were running high in a dispute about a reference Peirce had inserted into a paper by J. J. Sylvester. Yet probably of greater concern to Peirce was the fact that his divorce from Zina was drawing near. The final decree was issued on 24 April and six days later he married Juliette. On the day of his divorce he had written to Gilman that something had gone wrong at the Survey, that he could not make his afternoon class and that it might be best to bring his lectures that term to a close. It was surely not coincidental that Superintendent Hilgard had issued instructions on the 23rd directing him to go to Europe to help connect English and American pendulum work and to obtain additional, specially constructed pendulum apparatus. Peirce’s fifth, and last, European assignment must have come as a great relief, for it gave him and Juliette the opportunity to honeymoon away from the reproachful societies of Baltimore and Washington. Yet Peirce was diligent in executing his duties during his four months in Europe. He compared the Survey's standard yard No. 57 with the imperial yard No. 1 and with the iron yard No. 58 at the British Standards Office in London (where he also visited the library of the Royal Society). At the Kew Observatory in Surrey he measured the flexure of the pendulum base used for his 1878 experiments, which he had been unable to measure in 1878, and in Geneva he measured the flexure of the table he had used for the pendulum base in his 1875 experiments.
Part of Peirce’s European assignment was to obtain special pendulum apparatus from Gautier, world-renowned manufacturer of precision instruments in Paris (where, at the Bibliotheque Nationale, he made a thorough study of Paris MS. No. 7378, the Epistle of Petrus Peregrinus on the lodestone). He had known for some time that the four pendulums made at the Coast Survey Office were sufficiently defective to diminish the accuracy of measurements and he was much pleased with the prospect of having Gautier construct new pendulums, which he intended to take back with him in September. But during some preliminary experiments at the Gautier workshop he discovered a new source of error, the result of the flexure of the pendulum staff due to cuts about the knife-edges. He designed an improved staff to eliminate this flexure and he received permission to have the pendulums redesigned. Unfortunately, manufacturing delays and the necessity for continued experimentation during the manufacturing process resulted in Peirce’s return to America without the new pendulums. He unsuccessfully sought to obtain them after his return but was forced to continue using the old Peirce pendulums, thus depending on theoretically derived correction formulas. His failure with the Gautier pendulums no doubt contributed to Peirce’s embitterment and growing estrangement from the Survey.
Having settled in Baltimore with Juliette after his return from Europe in September 1883, Peirce resumed the direction of pendulum work for the Survey and was soon conducting experiments at the Washington Office and at the Smithsonian Institution. Probably due to his lengthy stay in Europe, Peirce did not make any presentations to scientific associations during the year, although a number of his scientific papers appeared in print. Nature published his "Note on Peirce’s comparison of U. S. Yard No. 57 with British Yard No. 1" (P 249), and the 1881 Coast Survey Report, published in 1883, contained his "Flexure of Pendulum Supports" (item 75), "Deduction of the Ellipticity of the Earth" (item 76), "Method of Observing the Coincidence of Vibration of Two Pendulums" (item 77), and "Value of Gravity at Paris" (item 15). Peirce’s fieldwork was, as usual, detailed in the Report's "Pendulum observations" (P 252). The 1882 Report was also published in 1883 and it contained the "Report of a Conference on Gravity Determinations, held at Washington, D. C., in May 1882" (items 48-55), which Peirce had edited and to which he contributed his "Six Reasons for the Prosecution of Pendulum Experiments" (item 51) and the "Opinions" section (item 54).
1884 was probably the worst year of Peirce’s life. On 26 January he was informed of a resolution of the Executive Committee of the Johns Hopkins that led to his dismissal a few months later. For several weeks, even months, Peirce was in a state of shock over the realization that his life's ambition had been shattered. Except for pendulum operations at the Smithsonian that continued under his direction through April, Peirce seems to have taken up no new Survey work until July when he received instructions from Hilgard to proceed to Fortress Monroe, Virginia, for gravity determinations and then to reconnoiter for one or two more stations in the mountains of Virginia, West Virginia, and North Carolina. Peirce was pleased with the results of his work at Fortress Monroe but he did not succeed in finding any new gravity stations. When Peirce returned to Washington he was put in charge of the Office of Weights and Measures.
Peirce finished the year with what seems to have been a burst of energy. Having resolved himself to a non-academic life, perhaps he was settling into his life as a scientist. He occupied the Smithsonian through February 1885 and measured (by comparing with standards) all four of the Peirce pendulums. As head of the Office of Weights and Measures, he traveled to Boston, Providence, Hartford, New York, and Philadelphia and met with electricians and manufacturers of gauges and machinery to determine how to meet the need for standards of measure as set out in resolutions passed at the United States Electric Conference. At the October meetings of the National Academy of Sciences in Newport he read three papers: "On Gravitation Survey" (P 281), "On Minimum Differences of Sensibility" (P 282), co-authored with Joseph Jastrow, and "On the Algebra of Logic" (P 283). He also discussed Wolcott Gibbs's paper "On the Theory of Atomic Volumes" and R. Pumpelly's paper "On an Experimental Composite Photograph of the Members of the Academy."
On 30 December he attended the American Metrological Society meeting at Columbia College, where he read a paper on the determination of gravity (P 270) and gave an account of his measures of the Old Stone Mill at Newport. A short article on the Mill had appeared in the 5 December issue of Science (P 293). In a discussion of the adequacy of the standards of weights and measures in the United States, Peirce informed the Society of some of the deficiencies of the current system. As a consequence, the Society passed a resolution calling for the appointment of a committee to persuade Congress and the Secretary of the Treasury of the need for establishing an efficient national bureau of weights and measures.
Possibly the most important of Peirce’s scientific writings of 1884 was his "Determinations of Gravity at Allegheny, Ebensburgh, and York, Pa., in 1879 and 1880" (P 290), which appeared as Appendix 19 of the 1883 Report. His Photometric Researches of 1878 (W3: item 69) figured prominently in volume 14 of the Annals of the Astronomical Observatory of Harvard College, entitled Observations with the Meridian Photometer, by Edward C. Pickering (P 271). And in November 1884, he published a paper on "The Numerical Measure of the Success of Predictions" (P 292) in Science, which illustrates that his interest in finding suitable means for quantifying even the evaluative elements of scientific work continued after his earlier work on the economy of research.
In bringing the picture of Peirce’s scientific activities to the end of 1884 we have gone somewhat beyond the period of the present volume. Yet it should be noted that as the present period ends and as Peirce came to accept the end of his academic career, he experienced something of a resurgence of his enthusiasm for experimental science. For a few months, until scandal shook the Survey, he may have thought that goodwill toward him might be restored. But, as will be seen in the introduction to the next volume, that was not to be.
The Johns Hopkins
Though Peirce’s decision to teach logic at the
Johns Hopkins was a diversion from the scientific path he had been
following so successfully, it did not set him on a new path of inquiry.
As he had clearly shown in his January 1878 letter where he had set down
his views on how the physics department should be organized, logic had
long been his abiding research interest. Some of his earliest writings
were about logic, broadly conceived to include the study of scientific
method as well as the more formal investigations of the syllogism and
the algebra of logic. His first major series of lectures, the Harvard
Lectures of 1865, was on the logic of science, and by the
following year he had begun chapter 1 of a treatise on logic where he
had pointed out that, although formal logic may seem trivial, it has in
fact such a deep significance that "the commonest and most indispensible
conceptions are nothing but objectifications of logical forms" (W1:351).
Six years later, spurred on by the seminal deliberations of the
Cambridge Metaphysical Club, Peirce was at work on his Logic of 1872-73,
with "logic" now defined as "the doctrine of truth, its nature and the
manner in which it is to be discovered" (W3:14). Although his focus had
shifted somewhat from the formal to the pragmatic aspects of inquiry,
his general interest still was logic. There is good reason to believe
that his famous "Illustrations of the Logic of Science" of 1877-78 was
the fruition of the 1872-73 work. Peirce expected to finish the
"Illustrations" as the period of the present volume got underway and to
publish them in book form in the International Scientific Series. The
sixth paper had appeared in the Popular Science Monthly in August
1878 and the French version of the second paper appeared in January
1879. As late as 1881 he wrote to his mother that he was thinking of
writing more papers for the series and in early 1882 he wrote, in the
front of a diary listing his expectations for the year, that he intended
"to write my book on logic." With this in mind, and remembering his
1867 American Academy Series (W2: items 2-6) and his pioneering 1870
"Description of a Notation for the Logic of Relatives" (W2: item 39), it
is clear that when Peirce took up logic at the Johns Hopkins, he was
continuing a well-established line of research. Already, W. K. Clifford
had declared Peirce to be "the greatest living logician, and the second
man since Aristotle who has added to the subject something material."
But in January 1879, even with the "Illustrations" still underway, neither logic nor philosophy in general was much on Peirce’s mind. He was hard at work on his spectrum meter experiments and plans for his extensive Pennsylvania fieldwork for the Survey, and he was under considerable pressure to finish his report on gravity at initial stations (item 13) and some other field reports. Almost all of Peirce’s 1879 writings, until he took up his position at the Johns Hopkins in the fall, reflect these scientific interests. The only exceptions are his short review of Read's Theory of Logic (item 1) and his lecture on logic and philosophy (item 3) which he may have delivered to the Harvard Philosophical Club in May. But this soon changed. On 27 July, he wrote to President Gilman that he was preparing his first lectures—"You would be amused if I were to say that they were very fine"—and soon afterwards he was deeply engaged in some of his most original logical researches. Not for several years—not until after his dismissal from the Johns Hopkins—did his philosophical research extend once again beyond logic to phenomenology and metaphysics.
Before turning to a chronological account of Peirce’s life at the Johns Hopkins, a few general historical remarks should be made. The Johns Hopkins University opened in 1876, financed by a bequest of the Baltimore philanthropist who gave the university its name. On the advice of the presidents of some leading universities, the trustees decided to focus on the establishment of professional schools and to emphasize research and graduate education. Daniel C. Gilman had been appointed president the year before, and he began to put together his faculty according to the trustees' plan. He was so successful that Peirce could announce, in his Fourth of July address to Americans in Paris in 1880 (item 16), that the Johns Hopkins was unique among American universities in that "it has here alone been recognized that the function of a university is the production of knowledge, and that teaching is only a necessary means to that end." In its first four years, the published results of research done at the Johns Hopkins nearly equaled the total research output of all American universities for the preceding twenty years.
Eighty-nine students were enrolled in 1876 and, three years later, when Peirce took up his appointment, enrollment reached 159. Many of the early students had already taken degrees from other universities, and at Hopkins they sought advanced degrees. Johns Hopkins was the first university in America to offer the doctorate. Many brilliant students made their way to the university during the early years, and some of the fifty or so who studied with Peirce who stand out include John Dewey, Fabian Franklin, Benjamin Ives Gilman, Joseph Jastrow, Christine Ladd (Franklin), Allan Marquand, Oscar Howard Mitchell, and Thorstein Veblen. Christine Ladd, with whom Peirce kept in touch throughout his life, was among the most gifted of his students. The admission of a woman for an advanced degree was remarkable for the times, although Ladd had been admitted under some pressure from James Joseph Sylvester, professor of mathematics and one of the university's chief luminaries, and on the recommendation of Benjamin Peirce. But when time came to confer Ladd's degree, the trustees broke the promise implicit in her admission; her doctorate was not conferred until many years later.
The Johns Hopkins was an intimate community during this period, for besides the students, the number of professors, lecturers, associates, and instructors ran to only about forty. Peirce stood out in these circumstances. In his life of Gilman, Fabian Franklin remarks that "the singular genius of Charles S. Peirce was made a source of remarkable intellectual stimulation in the University", 14 and Christine Ladd reported that in the classroom "Peirce . . . had all the air . . . of the typical philosopher who is engaged, at the moment, in bringing fresh truth by divination out of some inexhaustible well." 15 When Sylvester asked one of his students to tell him about Peirce’s lectures, he was informed that they "were always substantial, often very subtle, never trite, not easy to follow, frequently so lacking in clearness that the hearers were quite unable to understand"; but the student added that "there can be no question that Mr. Peirce is a man of genius." "Well," Sylvester replied, "if he is a genius, isn't that enough? Isn't it men of genius that we want here?" 16
Sylvester too, was a man of genius and the most distinguished professor during the university's early years. Although he had been shut out of university life in England, his reputation as a mathematician was of the first order. He had once held a post at the University of Virginia but had been forced to resign after an unfortunate incident with a violent student. Benjamin Peirce, perhaps the only mathematician in America who truly comprehended Sylvester's greatness, had urged Gilman to appoint him. Gilman had hesitated because he thought that Sylvester might be "hard to get on with" 17 but came to realize that he was precisely the kind of stimulating intellect needed to ignite the minds of advanced students. Sylvester was on the faculty when classes began in 1876. When he left seven years later to become Savilian Professor at Oxford, Gilman was probably beginning to reach his limit with the difficult natures of men of genius. He had just seen Sylvester and Peirce through a troublesome public quarrel and he now had to deal with the revelations and deliberations that would lead to Peirce’s dismissal not long after.
Sylvester fully lived up to Gilman's expectations. Under his leadership Hopkins became the center of mathematical research in America; in fact, it might be said that American mathematics, as a true contender on the world stage, was born there during Sylvester's tenure. (Earlier, perhaps only the work of Benjamin Peirce had gained international respect.) Although it may have been in the classroom that Sylvester sowed the seeds for the mathematical harvest that would follow, it was his founding of the American Journal of Mathematics (again with the help of Benjamin Peirce) that quickly put the Johns Hopkins at the center of mathematical thought. With the very first issue in 1878 the Journal became the forum for original mathematical research in America, and it served to connect American work with work from abroad.
Although it was Sylvester who galvanized the mathematical community at Hopkins, he was by no means the only creative force. Sylvester had helped persuade Peirce and Thomas Craig to stay on at Hopkins—as Coast Survey employees they were finding it difficult to fulfill the duties of two offices—and in March 1881 he wrote to Gilman:
"Allow me to express the great satisfaction I feel in the interest of the University at the measures adopted by the Trustees to secure the continuance of Craig and Peirce. We now form a corps of no less than eight working mathematicians—actual producers and investigators—real working men: Story, Craig, Sylvester, Franklin, Mitchell, Ladd, Rowland, Peirce; which I think all the world must admit to be a pretty strong team."
And when Professor Arthur Cayley of Cambridge University came as a visiting lecturer from January to June 1882, it is doubtful that as much sheer mathematical power was so concentrated anywhere else.
The other Hopkins professors during Peirce’s time were Basil L. Gildersleeve (Greek), Newell Martin (biology), Charles D. Morris (Latin and Greek), Ira Remsen (chemistry), and Henry A. Rowland (physics). Peirce seems to have had little interaction with Gildersleeve, Martin, Morris, and Remsen, although all except Morris read papers to the Metaphysical Club, which Peirce presided over for several terms. In the spring of 1880, Gildersleeve travelled to Europe with Sylvester and Peirce, and on 15 July wrote to Gilman from Paris that he had been seeing a good deal of Peirce, who "has been kind to me in his way, and if he were always as he can be sometimes, he would be a charming companion." But apparently no regular friendship developed. Relations were much closer with Rowland, chairman of the Physics Department, the position Peirce had sought in January 1878. Peirce often saw Rowland at the meetings of the Johns Hopkins Scientific Association and the Mathematical Seminary and he frequented and probably used Rowland's laboratory. When Rowland undertook to map the solar spectrum he used the results of Peirce’s work on the absolute wave-length of light, which, combined with the results of Ångström and Louis Bell (Rowland's assistant), gave him his table of solar spectrum wave-lengths that served as the world standard for a generation. 18
Three lecturers at the Johns Hopkins must be mentioned as influential in Peirce’s career: G. Stanley Hall, George S. Morris, and Simon Newcomb. The first two were on the philosophy faculty and taught in alternate half years. Morris taught ethics and the history of philosophy and Hall taught courses in psychology and developed the psychological laboratory. Although Morris, Hall, and Peirce were rivals for the philosophy professorship, there seems to have been no animosity among them, and Peirce’s relations with Hall, who for a time lived just across the street from him, were quite friendly. They both had an active interest in experimental psychology and they appreciated each other's work. In an 1879 article in Mind on "Philosophy in the United States," Hall had praised Peirce as "a distinguished mathematician" whose Popular Science Monthly "Illustrations" promised to be "one of the most important of American contributions to philosophy." 19 In 1884, when Hall was chosen over Peirce and Morris (and also William James) for the philosophy professorship, he expressed surprise: "Each of the three was older and abler than I. Why the appointment, for which all of them had been considered, fell to me I was never able to understand unless it was because my standpoint was thought to be a little more accordant with the ideals which then prevailed there." 20 Hall went on, in 1889, to become president of Clark University which he modeled after the Johns Hopkins. Peirce visited him there at least twice.
Simon Newcomb, a protégé and friend of Benjamin Peirce, was well-known to Charles. Their paths had often crossed, in and out of the Peirce home, and would continue to cross for years. They corresponded for over thirty years, with Peirce’s last letter to Newcomb dated 7 January 1908. 21 But more often than one might expect of a presumed friend, and more often than anyone realized, Newcomb took actions that damaged Peirce. Three incidents stand out. The first concerns Newcomb's role in the events leading to Peirce’s dismissal which will be discussed later. The second occurred after Peirce’s dismissal when Newcomb had succeeded Sylvester as editor of the American Journal of Mathematics. The first part of Peirce’s "Algebra of Logic" (P 296), which had been accepted for publication by Sylvester, appeared in the Journal in 1885, and part 2 was to follow in the next issue. Confident that it would be published, Peirce had duly submitted it, but Newcomb rejected it on the ground that its subject was not mathematics. Given that in the first part Peirce had introduced quantifiers into his system of logic, as well as truth function analysis, Newcomb's rejection can only be seen as a great misfortune for Peirce and for logic. The third incident occurred years later when Newcomb was asked to review a scientific monograph that Peirce had prepared for publication for the Coast Survey—the report on gravity at the pendulum stations Peirce began occupying in 1885. He had spent years reducing his data and writing this report and he expected it to be a major contribution. But two of three reviewers recommended that it not be published, with Newcomb's negative appraisal perhaps the deciding one. The rejection of Peirce’s report contributed to the decision to ask for his resignation from the Coast Survey. It is ironic that in his last letter to Newcomb, Peirce asked that he put in a good word for him at the Nation, which had long been an important source of income for Peirce, "if you are disposed to do me such a good turn."
In his five years at the Johns Hopkins, Peirce taught logic courses each semester, often both elementary and advanced courses. He also taught special courses on the logic of relatives, medieval logic, philosophical terminology, and probabilities, as well as a course on the psychology of great men. Never before in America—nor anywhere else, save perhaps at Aristotle's Academy in Athens—had a logician of such power developed a program of research with such capable students. It seemed certain that Gilman would see the results he had hoped for when he took a chance with Peirce. The expectation was widespread. According to John Venn:
"Mr. C. S. Peirce’s name is so well known to those who take an interest in the development of the Boolian or symbolic treatment of Logic that the knowledge that he was engaged in lecturing upon the subject to advanced classes at the Johns Hopkins University will have been an assurance that some interesting contributions to the subject might soon be looked for." 22
Venn was reviewing the 1883 Studies in Logic, of which he said that "such assurance is justified in the volume under notice, which seems to me to contain a greater quantity of novel and suggestive matter than any other recent work on the same or allied subjects which has happened to come under my notice."
Peirce’s involvement in the life of the university extended
far beyond the classroom. He attended the meetings of the Mathematical
Seminary and the Scientific Association and occasionally contributed
papers. Not long after he had arrived at the Johns Hopkins, he
instigated the founding of the Metaphysical Club, perhaps inspired by
his memory of the old Cambridge Metaphysical Club. He had conceived it,
according to Christine Ladd, in this way: "So devious and unpredictable
was his course that he once, to the delight of his students, proposed at
the end of his lecture, that we should form (for greater freedom of
discussion) a Metaphysical Club, though he had begun the lecture by
defining metaphysics to be 'the science of unclear thinking'."
"1. Reading of Minutes.
2. Reading & discussion of a Principal Paper, the delivery of which shall not exceed
forty-five (45) minutes.
3. Papers deferred from previous meetings.
4. Reading & discussion of Minor Communications, the delivery of which shall not exceed twenty (20)
minutes.
5. Reviews of books & magazines.
6. Transaction of business.
7. Adjournment"
Peirce served as president for about half the club's life, the other half being divided between Hall and Morris. He attended nearly two-thirds of the meetings and as late as 13 May 1884, long after it was known that his contract would not be renewed, he presided over the thirty-ninth meeting in the absence of Hall. He delivered his final paper to the club at its 40th meeting on 18 November. By this time Hall had been appointed to fill the philosophy position as professor of psychology and pedagogy, and he recommended at the 40th meeting that the Metaphysical Club should be reorganized to reflect the changes in the philosophy program. The club met only three more times, expiring with the 43rd meeting of 3 March 1885, not long after Peirce’s departure.
It is not surprising that most of Peirce’s research during the period of this volume, except for science, closely follows the paths marked out by his Hopkins courses and activities. Even the impact of his father's death on his program of research was influenced by Sylvester, who urged him to edit Linear Associative Algebra for publication in the Journal. Peirce’s interest in carrying on some of his father's mathematical work became much intertwined with interests related to the mathematical community at Hopkins, which included some of his best logic students.
During his first semester he taught a general logic course that met three times a week for three months and a course in medieval logic which met only once a week. Fourteen students took general logic, including three who would make contributions to Studies in Logic: B. I. Gilman, Ladd, and Marquand. It was the lectures for this course that Peirce was preparing when on 27 July he wrote to Gilman that "you would be amused if I were to say that they were very fine." Earlier in the letter, Peirce had expressed some anxiety about the coming term:
"I have a good deal of confidence & a good deal of diffidence about my instruction in Logic. The former about the ultimate result if I succeed in pleasing you the first year, the latter about the first year. Logic is peculiar in this respect that it is not so much a body of information as it is knowing how to use the mind. That is why the Socratic method ought to be followed as much as possible. But then it is extremely difficult to make that method work right."
From lecture notes and course descriptions, and from class notes taken by Allan Marquand and other students, we can get a fairly clear picture of what Peirce’s courses were like and what he was like as a teacher. Christine Ladd-Franklin speaks of the eagerness of Peirce’s students for intellectual adventure and their receptiveness "to the inspiration to be had from one more master mind."
"He sat when he addressed his handful of students (who turned out afterwards, however, to be a not unimportant handful) and he had all the air . . . of the typical philosopher who is engaged, at the moment, in bringing fresh truth by divination out of some inexhaustible well. He got his effect not by anything that could be called an inspiring personality, in the usual sense of the term, but rather by creating the impression that we had before us a profound, original, dispassionate and impassioned seeker of truth." 24
Joseph Jastrow reports that "Peirce’s courses in logic gave me my first real experience of intellectual muscle." He goes on to speak of Peirce’s "fertile suggestiveness" and then of his personality.
"Mr. Peirce’s personality was affected by a superficial reticence often associated with the scientific temperament. He readily gave the impression of being unsocial, possibly cold, more truly retiring. At bottom the trait was in the nature of a refined shyness, an embarrassment in the presence of the small talk and introductory salutations intruded by convention to start one's mind. His nature was generously hospitable; he was an intellectual host. In that respect he was eminently fitted to become the leader of a select band of disciples. Under more fortunate circumstances, his academic usefulness might have been vastly extended. For he had the pedagogic gift to an unusual degree. . . .
"The young men in my group who were admitted to his circle
found him a most agreeable companion. The terms of equality upon which
he met us were not in the way of flattery, for they were too spontaneous
and sincere. We were members of his "scientific" fraternity; greetings
were brief, and we proceeded to the business that brought us together,
in which he and we found more pleasure than in anything else."
In reflecting on the courses she had taken with Peirce, Christine Ladd-Franklin remarked that "His lectures on philosophical logic we should doubtless have followed to much greater advantage if he had recommended to us to read his masterly series of articles on the subject which had already appeared in the Popular Science Monthly." 26 But Marquand's notes of Peirce’s first classes show that, even if his "Illustrations" were not required reading, he often referred to them and spent his first three lectures discussing such topics as doubt and belief, methods of fixing belief, and degrees of clearness of ideas. This was the early part of the course Peirce called prolegomena, which continued through the eleventh class on 3 November. The final four paragraphs of Marquand's notes on lecture 11 show Peirce’s concluding emphasis for this part of the course:
"Various forms of investigation of the same subject converge to one result. Eg on velocity of light. This gives a real significance—a finality to truth. It is no (made up) figment, but a reality.
"We do not make Reality independent of thought altogether, but only of the opinion of you I or any other man. We may adopt a false opinion, this only delays the approach of the true.
"Truth we may call a predestinate opinion—sure to come true. Fatalism proper assumes events as sure to come to pass, no matter what we do about it. But our reaching this opinion tomorrow or next year does depend upon what we do. Its characters nevertheless are independent of our opinion.
"To say that real things influence our minds & that opinion will finally become settled—one & same. No explanation to say we come to same conclusion because real things influence our minds. We come to this final opinion by a process. What is that process, is the problem of Logic which we now consider."
Peirce continued the course with a lecture and a half on his theory of signs, taken mainly from hisJournal of Speculative Philosophy series of 1868 (W2), and then he took up formal logic, which he divided into syllogistic, the theory of logical extension and comprehension, the quantification of the predicate, and the algebra of logic. The first three topics took Peirce to the end of the term (of thirty lectures). The algebra of logic was reserved for the second term.
Peirce’s lectures on formal logic were based in part on his 1867 American Academy series (W2), but many new issues were developed which helped set the course for future work. For example, in order to examine reasoning in the theory of numbers, Peirce developed an axiomatic treatment of elementary number theory. In his 17 December lecture he gave the following seven premises:
"1. Every number by process of increase by 1 produces a
number.
2. The no. 1 is not so produced.
3. Every other number is so produced.
4. The producing & produced nos. are different.
5. In whatever transitive relation every no. so produced stands to that which produces it, in that relation
every no. other than 1 stands to 1.
6. What is so produced from any individual no. is an individual no.
7. What so produces any individual no. is an individual no."
Then, after specifying his notation and defining the relations "greater than" and "not greater than," he went on to develop examples. Items 24 and 38 show that Peirce continued to refine his basis for natural numbers.
Marquand's notes illustrate that Peirce used his classes to work through material that he was preparing for publication—or that what he prepared for his courses ended up in print. Several of Peirce’s important writings on logic from this period correspond to the content of his courses. This is true of "On the Logic of Number" (item 38) as well as of "On the Algebra of Logic" (item 19). When Peirce began the second half of his first logic course on 12 January 1880, he indicated that he would be dealing with Boole's and Schröder's work and with his improvements on Boole. He also mentioned work by Leslie Ellis and his own "Logic of Relatives" and De Morgan's 1860 paper on the syllogism. But the material Peirce discussed in his winter 1880 classes was developed quite beyond his algebras of 1867 and 1870. In the fall or winter of 1879, Peirce worked out a systematic treatment of the algebra of logic entitled "On the Algebraic Principles of Formal Logic" (item 6). Although this work is fragmentary, it suggests a systematic presentation of the algebra of logic that may have served both as an outline for his class lectures and for item 19. Even though item 6 is no doubt an early version of item 19, it is of interest to look at some of the differences. In item 6 Peirce still employed his 1870 notation, using the claw (–<) as his sign for general inclusion, "+," for logical addition, and "," for logical multiplication. In item 19, however, he has replaced the "+," with the simpler "+" and the "," (for logical multiplication) with "x" (or mere conjunction) though he retains his claw, as he will for the rest of his life (except in his graphical notations). The most powerful rule in the earlier system is a principle of duality that permits the assertion of a dual form for every well-formed expression. This rule is not present in the item 19 system but in its place is a new, more powerful (and considerably more important) rule, related to the deduction theorem, that permits the assertion of inferences as inclusions and vice versa. As a general expression of this powerful rule Peirce asserted the identity of the relation expressed by the copula with that of illation, and said that this identification gives us the principle of identity (x –< x) and shows that the two inferences
x
y and
x
[therefore]z
[therefore] y
–<z
are of the same validity. By this rule modus ponens and conditional proofs are legitimized in item 19, but they are no part of the earlier work. Otherwise the systems bear marked similarities.
Item 19 did not appear in print until September 1880, though Peirce had completed it by April when he left for Europe on assignment for the Coast Survey. Thus within a few months' time, six at most, his system had evolved in the ways indicated above. Notably, what came in between was his first course in logic. We know from Marquand's notes that as early as 12 November 1879 Peirce had asserted that "the Copula expresses a transitive relation" and that on 3 December he pointed out that "later in theory than Syllogistic—springs also as all Logic, from transitiveness of Copula" and "we have already identified the illative sign with the transitiveness of the copula. A [therefore] B & A –<B. The resemblance more important than the difference." Although it is impossible to say how much Peirce’s interaction with his students influenced his writings, the above case (which is one of several that could have been given) is very suggestive of the sort of synergism that one might expect between a good teacher and good students.
Another topic that occupied Peirce during the winter of 1879 was the relationship between thinking and cerebration (or logic and physiology in his first logic course). Two versions of a paper on the subject, included in the present volume, are first chapters of a work on logic, perhaps the book he was preparing from his "Illustrations." This is suggested by the fact that one version of the paper (item 7) moves into a discussion of the settlement of opinion that is taken almost verbatim from the first "Illustration" (W3:242-57), even as both papers appear to be early versions of the first section of item 19. Perhaps Peirce had it in mind to somehow combine his "Illustrations" with his 1879-80 work on the algebra of logic and to make that his logic book in the International Scientific Series. 27 It should also be noted that Peirce began his first logic course with a discussion of the connection between logic and physiology.
Five students were enrolled in Peirce’s course in medieval logic, described in the Hopkins Circulars as "A course of lectures on Medieval Logic, designed to show the spirit and leading doctrines of the logic of the Middle Ages." Peirce had made a thorough study of the history of logic and was probably the most knowledgeable American in medieval logic, and his collection of medieval logic texts was unsurpassed in America. While he was teaching medieval logic, he also directed Marquand's study of Epicurean logic, especially of the Herculaneum papyrus of Philodemus's "On Methods of Inference." On Peirce’s recommendation Marquand made the first English translation which he submitted along with a commentary as his doctoral dissertation. A paper by Marquand on Epicurean logic, possibly the commentary part of his dissertation, was included in Studies in Logic. Peirce’s own study of Epicureanism, in guiding Marquand, may have planted the seed that a few years later, fed by his developing evolutionism, grew into the paper on "Design and Chance," the seed being the Epicurean doctrine of absolute chance, the view that a place for freedom was afforded by the uncaused swerve of atoms. 28
During the same term Peirce gave a paper to the Metaphysical Club on 11 November on "Questions Concerning Certain Faculties Claimed for Man" and, on 3 December he spoke to the Scientific Association on the four color problem (he is reported to have suggested improvements to the method of demonstration employed by A. B. Kempe). 29 Before the year was out, he reviewed Vol. 2, No. 3, of the American Journal of Mathematics for the Nation. He remarked that Hall's discovery (at the Johns Hopkins) of the effect of magnets on electric current (the Hall effect) could hardly be overestimated, and he took special note of Sylvester's stress on the importance of observation for the discovery of mathematical laws by saying that "there has been, perhaps, no other great mathematician in whose works this is so continually illustrated."
At the end of his first term Peirce wrote the 25 December
letter to Gilman about his "state of dangerous cerebral activity &
excitement." He returned in January to begin a very unsettling year,
albeit one of remarkable achievement. While confined to his quarters
with bronchitis during the first months of 1880, that he wrote "On the
Algebra of Logic (item 19)", in which he produced a system of logic that
with only slight augmentation provides a complete basis for logic.
Also in 1880 he wrote his short "A Boolian Algebra with One Constant" (item 23), in which he anticipated H. M. Sheffer's paper of 1913 that introduced the stroke function. 36 He also continued his work on number theory and in the winter following his father's death began working in earnest on associative algebras. By the end of the year Peirce had sketched out his proof that, in the words of Eric Bell, "the only linear associative algebra in which the coordinates are real numbers, and in which a product vanishes if and only if one factor is zero, are the field of real numbers, the field of ordinary complex numbers, and the algebra of quaternions with real coefficients." 37 The proof appeared as an appendix to his edition of Linear Associative Algebra (item 42).
The Metaphysical Club was especially active during the first half of 1880 with about twenty presentations, and a special meeting was called in May for Josiah Royce's "On Purpose in Thought," read in his absence. On 9 March Peirce had presented "On Kant's Critique of the Pure Reason in the light of modern logic," which appears to be one of the few papers in this period focussing directly on the fundamental philosophical questions which Peirce had developed in his 1867 American Academy Series but which he would not take up again for several years. The following abstract of the paper appeared in the April Circular:
"Mr. Peirce compared Kant's solution of the problem "How are synthetical judgments à priori possible?" with the solution given by modern logic of the problem "How are synthetical judgments in general possible?" He showed that the reply which Kant makes to the former question has its analogue with reference to the latter. This analogous answer to the second question is true, indeed, but is far from being a complete solution of the problem. On the other hand, the solution which modern logic gives of its question may be successfully applied to Kant's problem; but this does not enable us to discover the origin of the conceptions of space and time. The categories of Kant were next considered. The list given by him is built upon the basis of a formal logic which subsequent criticism has undermined and carried away. Nevertheless there really do exist relationships between some of those conceptions and logic on the one hand and time on the other. The explanation of these relationships in conformity with modern logic, though far more definite than that of Kant, is not altogether dissimilar to it."
An impressive record of the fertility of Peirce’s mind in 1880 can be found in a notebook, probably written during the summer while he was in Paris. Entitled "Logic of Relatives," MS 364 contains a remarkable set of ideas and developments, including notes on alternative copulas where Peirce first set out the idea for his single connective Boolian algebra, some suggestive moves toward his quantifier notation, a new set of seven axioms of number based on the "greater than" relation, and notes on his relative of simple correspondence that he used for his treatment of finite collections (see item 38). It is possible that, like items 20 and 22, these are notes toward a continuation of item 19, a continuation that was sidetracked by his father's death and by Schröder's criticisms of his distribution claims. As might be expected, the ideas Peirce developed in the summer made their way into his logic classes in the fall.
Peirce had begun 1880 teaching the second half of his first general course on logic, as well as a two-month course in probabilities. In connection with the latter he probably wrote his notes entitled "A large number of repetitions of similar trials" (item 14). But his courses appear to have been cut short by the illness that gave him the opportunity to finish item 19 before leaving for Europe in April.
Peirce had returned by 5 August and remained in Cambridge until after his father's death on 6 October. Although he had originally thought to skip the fall term at the Johns Hopkins (he had been authorized to stay in Europe until January), he now prepared for the full academic year. On 19 August he wrote to Gilman about his upcoming lectures:
"I wish to extend them through the whole year if possible, & if Patterson consents. I expect to make two courses, one very elementary and practical, the other to take up first the algebra of logic, then probabilities, and finally inductive logic. I have this summer made a discovery in logic which seems to me to be really important. I shall develop it in an early number of the Journal of mathematics; and shall explain it in my lectures."
The "Logic of Relatives" notebook (MS 364) provides clues as to what this discovery might have been: his successful axiomatization of the natural numbers or his definition of finite sets (item 38); his "A Boolian Algebra with One Constant" (item 23); or it might have involved quantification or truth values. Peirce continued his letter with a remark about "On the Algebra of Logic," which would soon be in print. "This paper which is appearing in the Journal will probably be in 3 parts and will cover over 100 pages. The first part appears in the number which is nearly ready. I think it would be well for me to put some of my copies on sale at Cushing & Baily's for the convenience of my students."
Although Peirce was despondent when he returned to Baltimore after his father's death, he pulled himself together for his two fall semester courses: elementary logic, which met twice a week with an enrollment of five, and advanced logic, which met three times a week with an enrollment of seven. Among the seven were all the contributors to Studies in Logic as well as Sylvester's favorite student, Fabian Franklin. The text for the first part of the advanced course (item 19) had been issued in September. One of Peirce’s assignments appears to have been the preparation of class notes, or notes on the text, to be handed in for his scrutiny and comments. Christine Ladd's notes reveal an intensive study of item 19, especially with regard to his extension of De Morgan's eight propositional forms. Peirce had remarked that if we admit "particularly of the predicate," the system of propositions must be enlarged; but he did not say how many propositional forms there would be in the completed system. In one of the early classes in the fall term he showed that there are fifteen states of the universe for two terms; he did not yet consider the empty universe as a sixteenth state. Ladd made an elaborate study of this matter and struggled with the problematic empty universe. Taking a hint from Fabian Franklin's application of binary notation to logical formulae, she worked out binary numbers for all the value combinations for two terms. Though reluctant, she felt compelled for reasons of symmetry to include the null case. It was not until she read an early version of her Studies in Logic paper to the Metaphysical Club in January 1881 that she had overcome her reluctance to imagine an empty universe. A table in that paper gives "the sixteen possible constitutions of the universe with respect to two terms," which is in effect the second order truth-table for the sixteen binary connectives (probably making its first appearance in print). 38
Peirce had resigned the presidency of the Metaphysical Club before leaving for Europe, thinking he would be away until January, but he was reelected in the fall when he returned early. On 14 December 1880 he suffered from a severe headache and sent a note to be read in his absence at the meeting that evening. He reported that he had made contact with the secretary of the Leipzig Academical Philosophical Club, which sought to establish a "better acquaintance between the Clubs" and that he had "lately received papers from professors Wundt, Schröder, J. J. Murphy, Venn, Jevons, MacColl, and others on various logical and psychological subjects." With his fellows club members, Peirce was in the inner circle of logic.
Yet at the height of his success as a logician he had not settled on a career in logic. His success as a scientist, combined with the pressures of his duties for the Coast Survey, had something to do with his hesitation to commit himself to logic, as did his father's advice that he stick with science, but probably the main reason was his unhappiness with his part-time status at the Johns Hopkins. On 18 December he wrote to Gilman that he intended to leave the university in the spring because of the difficulty with conducting two careers at once and that, given his "subordinate position" at the Johns Hopkins, he was unwilling to modify his connection with the Coast Survey. He intended to abandon the study of logic and philosophy and offered to sell his library (on those subjects) to the University for $550. Before the week was out Gilman accepted Peirce’s offer and, in his commencement day address on 22 February, he lauded Peirce and remarked on the importance of his collection. 39 But Peirce did not quit logic and philosophy and he soon deeply regretted the loss of his books. By November 1883 his efforts to secure special volumes for his research and his courses—most notably the Berlin Aristotle—and his attempt to buy back some of the books he had sold to the library had become a source of irritation to the library committee and of personal offense to Gilman.
When Peirce resumed teaching in January 1881 for his fourth term he expected it to be his last; for by 7 February the trustees had accepted his decision to leave. Had his elementary logic course with three students and his advanced course with six (including, again, B. I. Gilman, Ladd, and Marquand) been his last, he might have avoided the erosion of his welcome at the Johns Hopkins as well as the scandal of his dismissal, which closed academic doors later on. But by the end of March, Sylvester had prevailed on Gilman to keep Peirce (and Craig) and the trustees had agreed to raise his salary from $1500 to $2500. Peirce agreed to stay on, and soon he was again deeply engaged in his logical researches.
1881 was a very productive year for Peirce, especially
in logic. Probably in the spring, in connection with his advanced logic
class, he wrote his paper on the theory of probable inference, which
would later be included in Studies in Logic (item 64), and in the
summer he wrote "On the Logic of Number" (item 38) where, several years
before the equivalent axiomatizations of Dedekind and Peano,
An examination of the early volumes of the American Journal of Mathematics reveals that many of the contributions are entitled "Note on . . . " or simply "On . . . " and it is quite probable that many of Peirce’s short manuscripts of this period that have such titles were written with the Journal in mind. A number of these pieces did appear there (items 10, 19, 38, 41, and 42) although at least three of them are more substantial than ordinary notes, and several others (items 5, 15, 18, and 44) appear elsewhere, though they too in may originally have been written for Sylvester's Journal. Even Notes A and B in Studies in Logic may have been intended at first for the Journal, along with items 6, 32, 33. But it is also possible that some of these papers were written for presentation at one or another of the Johns Hopkins clubs, for many of their presentations had such titles, including Peirce’s "On Relations between Sensations" in April 1881 and Joseph Jastrow's "A Note on Mechanical Light" in April 1883.
Peirce was president of the Metaphysical Club for all of 1881 but was absent for two of its six meetings. At the meetings he attended he heard ten papers by among others, Ladd, Franklin, Davis, Marquand, B. I. Gilman, and G. S. Morris. These were mainly on logic (three were on induction) and psychology, but one by Burt was on Hegel's Philosophical Propaedeutic and Morris's was on "English Deism and the Philosophy of Religion." In November Peirce gave a paper entitled "A Fallacy of Induction" before the Scientific Association in which he examined some of Priestley's inferences concerning atomic weights and specific heats. 41
Peirce’s courses in the fall of 1881 had unusually low enrollment with only three students both in his elementary and his advanced logic course. (Thorstein Veblen was in the elementary course, and Davis, B. I. Gilman, and Mitchell in the advanced.) The courses were described in the July Circular as follows :
"1. An elementary course on General Logic, deductive and
inductive, including probabilities. This course will be designed to
teach the main principles upon which correct and fruitful reasoning must
proceed; and special attention will be paid to the discussion of the
significance and validity of those logical conceptions and maxims which
are current in literature and in law.
2. A course upon the methods of science. A sketch of
deductive logic and the theory of relative terms will lead to the study
of the methods of Mathematics. The theory of chances and errors will
next be expounded. Lastly, after the development of the general doctrine
of induction and hypothesis, the methods of reasoning in several of the
physical and moral sciences will be examined in detail."
By the end of 1881 Peirce was again fully committed to logic both as investigator and teacher, and his reputation was now such that his work was noticed almost as soon as it appeared. To his Preface in his Studies in Deductive Logic, dated 3 October 1880, W. Stanley Jevons added the following paragraph:
"To the imperfect list of the most recent writings on Symbolical Logic, given in this preface, I am enabled to add at the last moment the important new memoir of Professor C. S. Peirce on the Algebra of Logic, the first part of which is printed in the American Journal of Mathematics, vol. iii (15th September, 1880). Professor Peirce adopts the relation of inclusion, instead of that of equation, as the basis of his system." 42
Peirce’s paper (item 19) had been out less than three weeks. John Venn noticed the same paper at the 6 December 1880 meeting of the Cambridge Philosophical Society, in particular Peirce’s notation (which appeared just before Frege's). 43 But perhaps the most satisfying notice came in the 24 March 1881 issue of Nature where, in a piece entitled "Recent Mathematico-Logical Memoirs," Jevons claimed that: "The most elaborate recent contributions to mathematico-logical science, at least in the English language, are the memoirs of Prof. C. S. Peirce, the distinguished mathematician, now of the Johns Hopkins University, Baltimore."
Peirce’s classes in the spring of 1882 were better enrolled, for he had five students in each of his two regular classes, elementary and advanced logic. (Mitchell took both, and B. I. Gilman and Ladd repeated the advanced course.) Peirce also taught a short course on the logic of relatives, where items 45 and 46 may have originated (as well as Note B of Studies in Logic). Perhaps the best indication of what Peirce covered in his short course is his "Brief Description of the Algebra of Relatives" (item 43) which he composed in very short order at the beginning of the term, inspired by what he heard from his advanced logic students who were taking Sylvester's new course of lectures on universal multiple algebra. Peirce was convinced that Sylvester's universal algebra was only a case, or interpretation, of his own logic of relatives, and he decided to write out his system in a way that would demonstrate the identity. He especially wanted to present his logic of relatives in a manner that would interest Sylvester. Peirce’s "Brief Description" is dated 7 January and he had proof sheets in hand by the middle of the month. Even as he was writing his brochure he was in correspondence with Sylvester about some of the points he hoped to demonstrate. But Sylvester seems not to have been convinced—and he was not anxious to see the paper in print, as is evident from Peirce’s 6 January 1882 letter:
"I lay no more claim to your umbral notation than I do to the conception of a square block of quantities! What I lay claim to is the mode of multiplication by which as it appears to me this system of algebra is characterized. This claim I am quite sure that your own sense of justice will compel you sooner or later to acknowledge. Since you do not acknowledge it now, I shall avail myself of your recommendation to go into print with it. I have no doubt that your discoveries will give the algebra all the notice which I have always thought it merited and therefore I hope my new statement of its principles will be timely. I cannot see why I should wait until after the termination of your lectures before appearing with this, in which I have no intention of doing more than explaining my own system & of saying that so far as I am informed it appears to be substantially identical with your new algebra, & that it ought to be, for the reason that mine embraces every associative algebra, together with a large class—perhaps all—of those which are not entirely associative. I am sorry you seem to be vexed with me."
Just the day before Peirce had written to Sylvester trying to explain the "precise relationship of your algebra of matrices to my algebra of relatives." He concluded that "It, thus, appears to me just to say that the two algebras are identical, except that mine also extends to triple & other relatives which transcend two dimensions."
Arthur Cayley had arrived at the Johns Hopkins in December and in January began his half-year tenure as visiting lecturer. On 18 January he, Sylvester, and Peirce had delivered a special program of lectures to the Mathematical Seminary in celebration of Cayley's visit. Peirce’s paper, "On the Relative Forms of Quaternions" (item 44), was commented on favorably by Sylvester. On 16 January Peirce had added a note to his brochure, which was then in press, stating that on that day, for the first time, he had read Cayley's 1858 Memoir on Matrices and had discovered that his algebra of dual relatives had been substantially anticipated by Cayley although, he pointed out, "many of his results are limited to the very exceptional cases in which division is a determinative process." Peirce was beginning to fear that his brochure might somehow offend Sylvester, perhaps even Cayley. So on 7 February, when his printed copies arrived, Peirce sent one to President Gilman along with the following note:
"It occurs to me that it is possible that (although I am unable to see it at all) there may be some just cause of offense in my references on the last page to Professors Sylvester and Cayley. Of course, you will see none at first glance; but will you see them and find out 1st whether they think they see anything out of the way and 2nd whether if so it is merely the systematic arrogance of these Britishers or whether it is just. I will keep back the issue until I hear from you."
There must have been some objection, for Peirce never did distribute his brochure. But he no doubt taught its content in his course on the logic of relatives, and he used it in his logic class in the fall.
However frustrated Peirce may have been—on 7 January he wrote "Sylvester is a cad" in his diary, and in later years he remembered that he had "felt squelched" 44—his relations with Sylvester continued seemingly undamaged. On 5 March he again wrote to him: "I have a purely algebraical proof that any associative algebra of order n can be represented by a matrix of order n + 1 having one row of zeros, together with a rule for instantaneously writing down such a matrix." About the same time, Sylvester was seeing Peirce’s "On the Logic of Number" and his edition ofLinear Associative Algebra through the press. They appeared in the fourth volume of Sylvester's Journal with the Linear Associative Algebra stretching over two issues. In the second addendum to LAA, "On the Relative Forms of the Algebras" (item 41), Peirce inserted a reference to his problematic brochure, which suggests that he may have completed this addendum between 7 January, when he finished the brochure, and the middle of February, by which time he had decided not to distribute it.
Peirce’s summer was almost completely taken up with his scientific endeavors, especially his work with John Herschel and the construction of his new pendulums but also with his spectrum meter experiments and with his reports for the Superintendent. He was occupied, as well, with the legal preparations for his divorce from Zina. He commuted frequently Baltimore, Washington, and New York, and took occasional side trips on Coast Survey business including the ill-fated trip to Montreal and Albany.
Charles Darwin's death in April had rekindled discussions of the question of evolution. On 27 April T. H. Huxley had written for Nature:
"He found a great truth, trodden under foot, reviled by bigots, and ridiculed by all the world; he lived long enough to see it, chiefly by his own efforts, irrefragably established in science, inseparably incorporated with the common thought of men, and only hated and feared by those who would revile, but dare not." 45
When Peirce returned to Baltimore in September to begin his fall classes, he gave a public lecture (item 56) designed to convey "the purpose of the study of logic" and "remove some prejudices." He gave a general outline of his fall course (to meet four times a week) and made a strong pitch for liberal education:
"But when new paths have to be struck out, a spinal cord is not enough; a brain is needed, and that brain an organ of mind, and that mind perfected by a liberal education. And a liberal education—so far as its relation to the understanding goes—means logic. That is indispensible to it, and no other one thing is."
Reflecting on Darwin's achievements, he attributed them largely to his method:
"The scientific specialists—pendulum swingers and the like—are doing a great and useful work; each one very little, but altogether something vast. But the higher places in science in the coming years are for those who succeed in adapting the methods of one science to the investigation of another. That is what the greatest progress of the passing generation has consisted in. Darwin adapted to biology the methods of Malthus and the economists. . . ."
After several other examples of men who had adapted the methods of one science to the investigation of another, Peirce went on:
"in order to adapt to his own science the method of another with which he is less familiar, and to properly modify it so as to suit it to its new use, an acquaintance with the principles upon which it depends will be of the greatest benefit. For that sort of work a man needs to be more than a mere specialist; he needs such a general training of his mind, and such knowledge as shall show him how to make his powers most effective in a new direction. That knowledge is logic."
Peirce was beginning to see his task as that of applying the methods of logic, especially induction and hypothesis, to philosophy and science. Over the coming months he would reflect on the statistical method that had been so fruitful for Darwin and would make the bold surmise that chance is an active player in the evolution of the universe and its laws. The Epicurean seed would bear fruit.
Peirce’s logic class for the fall of 1882 (with fourteen students!) and the spring of 1883 (with seven) was remarkable. Jastrow stayed for both terms, and it is probably this course he was thinking of when he said that Peirce had given him his first real experience of intellectual muscle. Peirce considered the foundations and philosophy of logic, using his "Illustrations" as his text, and then took up modern formal logic and the algebra of logic, using as texts De Morgan's Syllabus of Logic and Schröder's Operationskreis des Logikkalkuls, with examples from many other sources. He then took up (1) the logic of relatives, using as texts his "Logic of Relatives" (item 39 in W2), "Algebra of Logic" (item 19), "Algebra of Relatives" (item 43), and his paper on the logic of relatives that would become Note B in the Studies in Logic (item 66); (2) mathematical reasoning, where he examined the nature of mathematical demonstration and studied "the methods of mathematical research" using the history of multiple algebra as his example; (3) the theory of probabilities, with Liagre's Calcul des Probabilités, Boole's Calculus of Finite Differences, and Ferrero's Metodo dei Minimi Quadrati as texts; (4) inductive reasoning, to which he devoted a large part of the course and for which he used his "Theory of Probable Inference" (item 64); (5) the nature of scientific reasoning, with Kepler's De motibus stellae Martis; (6) an inquiry into the validity of modern conceptions of the constitution of matter, with Meyer's Kinetische Theorie der Gase; and (7) in conclusion, he considered the relation of the new theory of logic to philosophical questions. This course was Peirce’s most ambitious bid for a permanent position as Professor of Logic.
Peirce continued his active participation in the Johns Hopkins clubs. He presided over the Metaphysical Club until November and gave a paper on Mill's logic and a response (item 47) to B. I. Gilman's "On Propositions and the Syllogism." In October he read "On a Class of Multiple Algebras" (item 57) to the Mathematical Seminary. He also presented two papers on logic to the National Academy of Sciences, one in April "On a fallacy of induction" (P 233) and another in November "On the logic of relatives" (P 235). The first may be the paper he had presented to the Johns Hopkins Scientific Association in November 1881, and the second is probably what became Note B in Studies in Logic.
By the end of 1882 Peirce was experimenting with graphical systems of logic. He may have been stimulated by Sylvester's 1878 paper "On an Application of the New Atomic Theory to the Graphical Representation of the Invariants and Covariants of Binary Quantics," perhaps in conjunction with his study of the atomic theory of matter for his logic class. In this paper, in what Peirce saw as an anticipation of his reduction thesis (see item 20), Sylvester had put forward "one simple, clear and unifying hypothesis, which will in no wise interfere with any actually existing chemical constructions. It is this: leaving undisturbed the univalent atoms, let every other n-valent atom be regarded as constituted of an n-ad of trivalent atomicules arranged along the apices of a polygon of n sides." After explaining his theory further, and giving numerous diagrammatic examples, Sylvester remarked: "The beautiful theory of atomicity has its home in the attractive but somewhat misty border land lying between fancy and reality and cannot, I think, suffer from any not absolutely irrational guess which may assist the chemical enquirer to rise to a higher level of contemplation of the possibilities of his subject." Peirce’s paper on junctures and fractures (item 59) and his 21 December letter to O. H. Mitchell (item 60) suggest that he may have been trying to apply some of the methods of chemistry, and perhaps the theory of atomicity, to logic.
Also in 1882, though perhaps already in the latter part of 1881, Peirce met Benjamin Eli Smith, who had come to the Johns Hopkins as a graduate assistant. Although he seems not to have been a student in any of Peirce’s courses, he presented two papers to the Metaphysical Club, one on "Wundt's Theory of Volition" in February 1882 and the other "On Brown's 'Metaphysics'" the following month. Smith was a member of the staff of the Century Dictionary (and soon became its managing editor) and he recruited Peirce to be a contributor. Peirce was given principal responsibility for terms in logic and philosophy, mathematics, mechanics and astronomy, weights and measures, and all words relating to universities. By 1883 Peirce had already begun working on definitions (see MSS 496 and 497) and in the fall of that year, with the dictionary project in mind, he added a new course on philosophical terminology. From this time onward—for after the first edition of 1889-91 he immediately set to work on a revised edition—Peirce had definitions, etymologies, and language groups (and other lexicographical matters) on his mind. This was a monumental project and Peirce’s contribution was massive. Its impact on the evolution of his thought was surely very significant, though it has yet to be seriously examined. Peirce’s difficulties with Sylvester had not ended with his decision to withhold his 1882 brochure. In the early weeks of 1883 a more severe and consequential dispute broke out. In August 1882 one of Sylvester's papers (an abstract of a paper on nonions which he had read in May to the Mathematical Society) appeared in the Circulars with the following sentence: "These forms can be derived from an algebra given by Mr. Charles S. Peirce (Logic of Relatives, 1870)." The sentence, as it turned out, had been written by Peirce. Apparently, Sylvester had entrusted Peirce with checking the proof-sheet of his paper for adequate reference to his own work. Peirce had expected that Sylvester would look over his changes before releasing the proof-sheet to the printer but, according to Sylvester, that did not happen. In reflecting on the episode in later years, 46 Peirce remembered that he had not made the insertion mark for the printer, but had only written out the sentence he thought Sylvester would want to insert. The February 1883 Circular carried an Erratum by Sylvester correcting the troublesome sentence to read "Mr. C. S. Peirce informs me that these forms can be derived from his Logic of Relatives, 1870." He went on to say:
"I know nothing whatever of the fact of my own personal knowledge. I have not read the paper referred to, and am not acquainted with its contents. The mistake originated in my having left instructions for Mr. Peirce to be invited to supply in my final copy for the press, such references as he might think called for."
Peirce was incensed. Not only had he engaged in lengthy discussions with Sylvester about his logic of relatives and carried on at least a limited correspondence with him, but in April 1882 Sylvester had discussed Peirce’s logic of relatives before the Mathematical Seminary and in the same month had stated specifically before the Scientific Association that Peirce’s logic was tantamount to his Nonions. His remarks had been reported in the Circulars as follows:
"Mr. Sylvester mentioned . . . that in his recent researches in Multiple Algebra he had come upon a system of Nonions, the exact analogues of the Hamiltonian Quaternions. . . .
"Mr. Charles S. Peirce, it should be stated, had to the certain
knowledge of Mr. Sylvester arrived at the same result many years ago in
connexion with his theory of the logic of relatives."
And only a year earlier, in Sylvester's own journal, Peirce had published the addendum to his father's Linear Associative Algebra (item 41) in which he proved "that any associative algebra can be put into relative form, i.e. . . . that every such algebra may be represented by a matrix."
Peirce wrote out a full reply to the Erratum and sent it to Gilman. There followed much correspondence between Gilman, Peirce, and Sylvester and there were drafts of responses and responses to responses. At one point, on 29 March, Peirce wrote to Gilman:
"I cannot consent to my statement being modified unless Professor Sylvester will say that my conduct was correct in regard to the proof-sheets. I have no objection to this being qualified by his saying that it was correct if the oral message was delivered to me as I say it was; but clearly if such a qualification is to be inserted, everything depends upon how it is put."
Peirce continued with detailed recommendations for emendation. At some point Gilman sent drafts of Peirce’s reply and Sylvester's note to Peirce’s reply to G. W. Brown, one of the trustees, to ask for advice. Brown replied on 17 April: "After thinking over this annoying matter it appears to me that nothing is to be done but to publish the articles as they stand. This should however be the last of it and would it not be well to say so to both in advance." Earlier there had been a suggestion, apparently from Brown, to publish Peirce’s reply without Sylvester's note. But Sylvester had responded heatedly to Gilman:
"I am astonished at the proposition contained in your note of the 18th that it should be proposed to allow Mr. Peirce’s virulent and disingenuous statements to be made in the circular without giving me an opportunity of replying thereto. If that course is adopted, self-respect will render it imperative for me to withdraw from all future participation in the circulars."
Peirce’s "Communication" (item 67) finally appeared in the April Circular, preceded by this "Note" from Sylvester:
"I wished (as I still wish) it to be understood that it is Mr. Peirce’s statement and not mine that the "forms" in question can be derived from his Logic of Relatives. I certainly know what he has told me and should attach implicit credit to any statement emanating from him, but have not the knowledge which would come from having myself found in his Logic of Relatives the forms referred to; as previously stated I have not read his Logic of Relatives and am not acquainted with its contents."
Many years later, when Peirce recounted these events, he wrote of Sylvester's character:
"Sylvester was a man whose imagination and enthusiasm were incessantly running away with him: he was given to harboring the most ridiculous suspicions and to making rasher assertions than became so great a man. His power of distinct recollection was most phenomenally weak, almost incredibly so; while his subconscious memory was not at all wanting in retentiveness. . . . I suppose, as he said, that he "came across" the system of novenions . . . and remembered, or thought he remembered, that I had pointed out these forms. Subsequently, he got a suspicion that I was about to charge him with plagiarizing my "Description of a Notation &c," and was anxious to declare that he had never read it, and knew nothing about it. He seems to have fancied that I had some deep-laid plot against him." 48
Peirce must have felt some relief from the tension of his conflict with Sylvester toward the end of March 1883 when his long-awaited Studies in Logic, which had been "in the works" for over two years, finally appeared. Peirce had written to Gilman about it as early as 9 February 1881, and on 8 December 1881 he had said to Christine Ladd that "after a long delay from various causes, I have everything arranged to go on with the publication of our essays except one thing—about $300 is still needed. I shall probably supply this myself, but am not prepared to do so now, so that the matter may rest idle till spring." Although the matter lay idle much longer, when it finally did come Studies in Logic the book was immediately recognized as an important contribution. The book as a whole covered a vast part of the field of symbolic logic and dealt with the work of the major contributors. Even Frege's Begriffsschrift appeared in Ladd's bibliography although it is not mentioned in the paper. In his review for Mind, Venn said that the most interesting paper philosophically, was the concluding one by Peirce which dealt with the nature and foundations of statistical reasoning and the connection between probability and induction. This was, of course, "A Theory of Probable Inference" (item 64) about which Peirce wrote to Paul Carus: "In my humble opinion you are never likely to say again anything so false as that writings lose their freshness by being worked over. The first page or two of my Theory of Probable Inference was put into more than 90 forms very varied before I was satisfied; yet nobody would suspect any elaborate work on it." 49
Peirce was pleased with Studies in Logic. He
sent out many inscribed copies as gifts and for the remainder of his
days he often referred to one or another of its papers as an
authoritative source. Probably with a complimentary copy, he wrote to
T. S. Perry: "If you are going to read any of my papers—which seems
inconceivable—I hope you will try note B in the bound book."
Studies in Logic is a landmark not only for logic, but also for education in America. It was a work on the leading edge of research in its field by a team of researchers composed mainly of graduate students. Certainly they were led by a seasoned scholar but he neither demanded nor wanted credit for their work. Even though Peirce edited the book his name did not appear on the title page; it was by MEMBERS of the the Johns Hopkins University. This was in the spirit of Johns Hopkins in its first decade.
Peirce had a great deal on his mind in the winter and spring of 1883. There was his demanding logic course, the trouble with Sylvester and, as always during these years, he had several Coast Survey projects going at once: pendulum operations at the Smithsonian and the Stevens Institute, testing of the new Peirce pendulums, preparations for an eclipse expedition, continuation of spectrum meter experiments and other metrological work, plans (which would fall through) to go to Point Barrow in the Arctic, and the constant pressure to finish overdue reports. He participated in the first three meetings of the Metaphysical Club and remarked on papers by G. S. Morris, A. H. Tolman, and W. T. Sedgwick. On May he wrote to Hilgard to say that he had "written for Science a careful review of Dr. Craig's work on projections—a job upon which I have spent a great deal of time"; but apparently it was never published and only one manuscript page (MS 442) has been found. Looming over all this, casting its shadow, was Peirce’s coming divorce and remarriage.
Peirce’s divorce from Zina became final on 24 April. Six days later he married Juliette and by 2 May they were sailing to Europe. Peirce had made plans to visit with Hugh MacColl in Boulogne, which he probably did near the beginning of his stay. On 16 May he sent Gilman a general plan for his 1883-84 course of lectures based, as he said, on his "forthcoming book." From the plan, Gilman had the following notice printed in the June Circular:
"Mr. C. S. Peirce. 1. Will give forty lectures to graduate and special students upon General Logic. The course will follow the contents of Mr. Peirce’s forthcoming treatise on logic. At least one lecture will be devoted to each chapter, but the preferences of the class will be consulted in deciding upon the topics of nine of the lectures. The distribution of topics in the chapters is as follows:
"Generalities (5 chapters)
Deductive Logic:
Non-mathematical (3 chapters)
Algebraic (4 chapters)
Otherwise mathematical (4 chapters)
Inductive Logic:
Theory (9 chapters)
Illustrations (6 chapters)
"2. Will give special courses or private lessons upon any branch of the subject in which any of the graduates or special students may desire instruction."
As the summer progressed Peirce expanded his plan into a full-fledged syllabus and, as it grew, so did the planned number of lectures. There are two manuscript versions of the syllabus, one with fifty lectures (MS 458) and a more finished one with sixty lectures (item 69). A few features of the syllabus stand out. Peirce has definitely introduced truth values into his system of logic by this time and he is using quantifiers as he will in his 1885 "Algebra of Logic." Most of the topics he had written about while at the Johns Hopkins are covered in one way or another. Possibly the best general outline we have of his logic of relatives is given in lectures X through XIV. Some lectures treat topics he had not yet written about but soon would. For example, part of lecture XIX is devoted to the nature of geometrical axioms and the last part of lectures XXXIII-XXXVI is devoted to the problem of the duration of play, applied to the theory of natural selection and to philosophy. Peirce’s thoughts were turning toward "Design and Chance" (item 79). There is even a provocative reference in lecture XXV to the harmfulness of logic too narrowly studied. Overall, the syllabus provides a detailed account of Peirce’s well thought out design for an advanced general course in logic.
There are four lectures or fragments of lectures that Peirce probably composed before classes began in the fall: items 70-73. In them he continues the discussion of the constitution of the universe begun in item 19 and in his class lectures (which Christine Ladd had developed in her Studies In Logic paper). Peirce’s theory of quantification is also much in evidence. At least the first three lectures were probably written while Peirce was still in Europe, though it is possible that all of them were written out class by class.
When Peirce and Juliette returned from Europe in mid-September 1883, they took a two-year lease on a house in Baltimore and began to furnish it. Peirce had sought and had been given Gilman's assurance that his position with the philosophy department was secure, so he and Juliette were eager to make Baltimore their home. When Peirce began teaching in the fall he may well have supposed that it was just the next of many teaching years ahead of him. It turned out that enrollment in his courses dropped dramatically from the previous year. Only four students took the advanced logic class in the fall—John Dewey, Jastrow, C. W. E. Miller, and Henry Taber—and only Jastrow and Taber were left for the second term. Dewey had dropped out because the course was too mathematical. But he and Jastrow enrolled in Peirce’s new course on philosophical terminology. The course met once a week and apparently lasted for only a few weeks. Beginning in early October, Peirce sought special privileges with the University Library. On 10 October he requested permission, for special reasons, to take out twelve books at a time. The special reason was that he was engaged in a "piece of work" that "requires me to make use of a great many books." He explained that his research required the regular consultation—in some cases many times a day—of certain books. "Such for instance is the Berlin Aristotle in 5 volumes." Probably the "piece of work" was his set of definitions for the Century Dictionary, but soon he was also stymied in his related course on philosophical terminology. Although he tried as best he could to work out a suitable arrangement with the library, he met with no success. Finally on 8 November he wrote to Gilman: "I find my work brought to a complete stand-still for the want of books. I have been obliged to suspend my lectures on Philosophical Terminology until I can obtain the Berlin Aristotle. My application to you to have the University add another Aristotle to the library I understand to be refused." Peirce went on to ask if he could buy back his books listed under Ancient Authors which he had sold three years earlier. Gilman must have taken offense for a week later Peirce wrote to him again: "I deeply regret having said anything which seems to offend you, since I am bound to you by every bond of official respect, personal esteem, gratitude, and if you will permit me to say so even affection." But Peirce continued in a less conciliatory way:
"Then, let me say with candour, my dear Mr. President, that although I believe I have never complained of it to anybody, I have not thought that any heed at all had been given to any of the suggestions which I have made in regard to wants in the Library, although I considered them important. . . . I think, without of course comparing you to the jailer of the Peabody Library, that Cambridge is a trifle ahead of Baltimore in its appreciation of the wants of its students in the way of books. You have always permitted me to express myself with great freedom to you, and I always think a misunderstanding should be seized as an occasion to have a mutual understanding. There[fore], I beg you will not find offence in what I am saying. I have lately been offending people everywhere by my speeches."
Peirce then withdrew his request, admitting that it had not been "in good taste or temper." Although it is not clear how the whole matter was finally settled, it does appear that the course on philosophical terminology had come to an end.
Peirce taught a third course in the fall of 1883, described very briefly in the Circulars: "He also guided a company of students in studying the psychology of great men." 52 He had invited a group of students to join him in this study, and they worked out an elaborate program that involved reading the chief biographies of the day, extracting data of specified sorts, compiling impressionistic lists of great men and finally, submitting the lot to statistical analysis. Peirce wanted to demonstrate that statistical analysis could be fruitfully applied even in situations where the primary data are impressionistic (based on impressions). This study may have been the first extended application of statistical methods to comparative biography. Although Peirce continued the study with his group of students through the summer and fall of 1884, and even into the winter, it was never completed. Sometime after his move to Milford in 1888 Peirce took up the study again, probably stimulated by the publication of The Comtist Calendar. His 1901 paper on "The Century's Great Men of Science" was an offspring of the earlier study, and shortly after Peirce’s death one of the members of Peirce’s group, Joseph Jastrow, remarked in a memorial article 53 that he had been permitted to publish two rather simple conclusions, one relating to "Longevity," and the other to "Precocity." 54 Although many of the manuscripts related to the study of great men were composed in the period of the present volume, the study as a whole went beyond the period and will therefore be included in the next volume.
Peirce attended all the meetings of the Metaphysical Club for the fall term and gave one paper, a reply to G. S. Morris's paper on "The Philosophical Conception of Life." Among several others, he heard Jastrow read a paper on "Galton's 'Inquiry into Human Faculty'," Dewey on "The Psychology of Consciousness," and A. T. Bruce on "The Design Argument." Bruce's paper was read on 11 December and the Club's minute book shows that Peirce remarked on it. Just over one month later Peirce would read his "Design and Chance" to the Club.
Looking through the correspondence of this period for clues to Peirce’s life and work, one letter stands out as signalling the end of his fortunes at the Johns Hopkins. On 22 December 1883 Simon Newcomb wrote to Gilman: "I felt and probably expressed some uneasiness in the course of our conversation the other evening, lest I might have been the occasion of doing injustice to persons whose only wrong had been lack of prudence. I have therefore taken occasion to inquire diligently of my informant, and am by him assured that everything I had said was fully justified." Newcomb was referring to Peirce as the one he might have injured and his informant was Julius Hilgard. Although it is not known for sure what "wrong" Peirce had committed beyond a "lack of prudence," we do know that Newcomb's revelations led to a resolution, of the Johns Hopkins Executive Committee that effectively ended Peirce’s connection with the university. The resolution passed on 26 January 1884, was not to renew the contracts of lecturers in philosophy and logic "after the present engagements expire" and to replace the three lecturers (Peirce, Morris, and Hall) with one Professor and an assistant. But only Peirce’s appointment expired at the end of the 1883-84 academic year, and he soon realized that the resolution was aimed at him. At first he appealed to the sense of fairness of the university administration. On 8 February he wrote to Gilman and asked that his letter be laid before the Executive Committee:
"On returning to Baltimore last September, I was unable to obtain a suitable house for one year. Therefore, as soon as the President returned I went to him and explained my difficulty and asked whether in his judgment it would be prudent for me to take a house for two years. To this important inquiry he replied that he knew of no disposition to disturb me in my place. The Treasurer suggested my purchasing a house. In view of these encouragements, I did take a house for two years. I have never heard the smallest whisper of dissatisfaction or suggestion of a possible change until I yesterday received your resolutions. My lectures have been much better than hitherto. There has been more coöperation between the different branches of philosophical instruction. There has, in short, been no reason for a change which did not exist before. I, therefore, appeal to your sense of fairness, gentlemen, with great confidence; for to cut short my lectureship at the end of this year, though it be perfectly within the letter of the contract, is not one of the things which it is open to you under the circumstances to do. I have no doubt that President Gilman spoke truly and sincerely in encouraging me to take my house. He now tells me he has for a long time seen this crisis coming; this long time must however have been altogether subsequent to last October."
The final paragraph of Peirce’s letter suggests that he thought religion was somehow at issue:
"I also desire to address you briefly upon the present state of philosophy, and to show you that the difficulty of finding a modus vivendi between philosophy, science, and religion, is now much less than it has been for a very long period; so that you have only to make the philosophical department really true to the actual condition of thought, and you will bring it into a state of warm sympathy and friendship with science on the one hand and with Christianity on the other."
Peirce was probably right on two counts. The immediate and official cause of the decision to let him go was something subsequent to October 1883, and probably something else, like his attitude about religion, had helped bring on the crisis. When Gilman had candidly told Peirce that he had "for a long time seen this crisis coming" he may have revealed a truth he would decline to make official. Certainly Peirce had given Gilman many reasons to be concerned about his long-term continuation at the Johns Hopkins beginning with his December 1879 letter about the alarming state of his brain. Peirce’s work for the Survey had resulted in a number of conflicts and absences and, perhaps partly because of the pressures of two jobs, his ill health had been a source of inconvenience. His aborted resignation in 1880 and the events following the sale of his books, and the cancellation of his course in philosophical terminology, had been irritating and perhaps even embarrassing for Gilman, who surely also noticed that Peirce’s courses often had low enrollments. And then there was the question of religion. Charles W. Nichols, who was in Peirce’s first course in logic and who presented the first paper to the Metaphysical Club, recorded some telling remarks in his "Johns Hopkins University Note Book":
"I read by invitation from the university, before the Johns Hopkins Philosophical Association, a thesis on "Illustrations from Grecian philosophy of the fallacy that differences in nature must correspond to received verbal and grammatical distinctions." Professor Charles S. Peirce, the scientist who presided, was an agnostic, and heartily seconded the sophomoric flaying I administered to old father Aristotle and the Schoolmen." 55
If Nichols's perception of Peirce was common among his students, it probably would have come to Gilman's attention and would have disturbed him. He had worked hard to alleviate the fears of conservative Baltimorians who imagined that the University was encouraging agnosticism.
But the official cause of the decision to let Peirce go, and clearly the provocation, was Newcomb's revelation. This is evident in the record of the Johns Hopkins Executive Committee. On 1 December 1884, Committee Chairman William Brown made the following statement:
"The undersigned having read Mr. Peirce’s recent letters to Judge Brown, & having refreshed their recollection by reference to the records of the Executive Committee, & the official correspondence, make the following statement so that if there should be any subsequent reference to this affair, their understanding of [it] may be on record.
"The change of attitude toward Mr. Peirce on the part of President Gilman, which is the cause of complaint, occurred near the beginning of January 1884 in consequence of information first brought to his knowledge in December 1883, several weeks subsequent to his remark that he "knew of no disposition to disturb Mr. Peirce in his relations to the university"; and from that time onward Mr. Gilman's communications to Mr. Peirce were governed by the action of the Executive Committee and were taken in consultation with two members of that body."
Newcomb's revelation never became part of the official record. The most explicit reference appeared in a 15 November 1884 letter from Gilman to the Executive Committee in which he summarized the events surrounding Peirce’s dismissal:
"It is true that [at] the beginning of the academic year 1883-4, I knew of no disposition to disturb Mr. Peirce in his relations to this university. It was not until several weeks later that one of the Trustees made known to the Executive Committee & to me certain facts which had been brought to his knowledge quite derogatory to the standing of Mr. Peirce as a member of an academic staff. These facts & their bearing upon the philosophical instruction in this university were considered by the Executive Committee, at their meeting, January 26, 1884."
Further light is shed on the matter by Newcomb himself in a letter of 30 December 1883 to his wife:
"I have been somewhat exercised at being the unintended means of making known some of the points of C. Peirce’s marital history at Baltimore. When last going to N. Y. I went from Balt. to Phil. in the same seat with Dr. Thomas, a J. H. U. Trustee, and supposing they all knew more or less of the affair got talking of it, and let several cats out of the bag. What I gave as reports, Dr. Th., I suspect, told Gilman as facts, and troubled the latter greatly, as it seems Mrs P (2) had begun to cultivate Mrs G's acquaintance. The supposition is, that the marriage last summer made no change in the relations of the parties. Mr. Hilgard assures me that it is all true, they having occupied the same apartments in N. Y. some years ago. It is sad to think of the weaknesses which may accompany genius." 56
An examination of the exchange of letters between Peirce and Gilman and other members of the Executive Committee, which began with Peirce’s notification of the 26 January resolution and continued at least into December, reveals that Peirce’s initial concern was to keep his position and to defend his honor as an instructor. But as he became aware of the unyielding resolve of Gilman and the Committee, his concern shifted to an interest in reimbursement for damages resulting from his dismissal. If anything beneficial came of that lengthy exchange of letters, it was at most some measure of compensation for his loss in setting up a home in Baltimore. But the loss of an academic career, both to Peirce and to the world, could not be compensated.
During that painful year Peirce must have suspected that his academic life was over. Although he made some attempts to find another teaching position, it was less than four years after his dismissal that he and Juliette moved to Milford, Pennsylvania, to live the rest of their lives in seclusion and relative obscurity. Peirce was never again offered a regular teaching position, and his dismissal from the Johns Hopkins was at least partly the reason. In dropping Peirce from consideration for a position in philosophy at the University of Chicago in 1892, William R. Harper relied on the advice of George H. Palmer of Harvard University, who had written on 4 June 1892:
"I am astonished at James's recommendation of Peirce. Of course my impressions may be erroneous, and I have no personal acquaintance with Peirce. I know, too, very well his eminence as a logician. But from so many sources I have heard of his broken and dissolute character that I should advise you to make most careful inquiries before engaging him. I am sure it is suspicions of this sort which have prevented his appointment here, and I suppose the same causes procured his dismissal from the Johns Hopkins." 57
It is remarkable that James, certainly a man of judgment and discrimination, never gave up on Peirce but continued to recommend him as both teacher and scholar. It is disturbing that others were so blind to what James saw in Peirce.
Peirce’s appointment at the Johns Hopkins ran until 1 September 1884, so he labored under the cloud, even disgrace, of his dismissal for about seven months. Yet he persevered with his classes and managed to keep up a steady flow of manuscript pages. In addition to his advanced logic course that continued in the second term with only two students (Jastrow and Taber), he taught a course on probabilities that met twice a week with an enrollment of seven (Davis, Julius J. Faerber, Arthur S. Hathaway, Jastrow, Henry B. Nixon, William E. Story, and Taber). He also gave several papers during the year including one to the Mathematical Seminary and three to the Metaphysical Club. On 16 January he delivered "On the Mode of Representing Negative Quantity in the Logic of Relatives" to the Mathematical Seminary. However, he could not have hoped to enlighten Sylvester about the generality and power of his logic, for Sylvester had departed for England the previous month to take up his chair at Oxford. He did not find out about Peirce’s dismissal right away and several years later (on 28 March 1888) he wrote to Gilman: "What was the cause of C. Peirce’s leaving? I am truly sorry on his account. I regret the differences which sprang up between him and me for which I was primarily to blame. I fear that he may not have acted with entire prudence in some personal matters."
On 17 January, the night after his talk at the Mathematical Seminary, Peirce gave what may be his most important philosophical paper of the Johns Hopkins period. On that night he presented "Design and Chance" (item 79) to nine members of the Metaphysical Club. The following remarks appear in the Club's minute book: "President Morris in the Chair . . . Principal paper was read by Mr. Peirce. Subject: Chance and Design. Mr. Peirce, Dr. Franklin, Prof. Remsen, Mr. Dewey and Mr. Jastrow as well as the President took part in the discussion." The paper is not such a substantial work in itself, but it represents an important turning point in the evolution of his thought. It is curious that it was written at such a turning point in his life. We shall quickly survey the rest of Peirce’s non-scientific papers for the remainder of the year and then return to "Design and Chance."
Peirce delivered his second paper of 1884 to the Metaphysical Club on 13 May. It was entitled "Logic of Religion." On 7 April he had written to Gilman to seek permission to give six lectures on the logic of religion in the fall "with the purpose of stating some things on the credibility of various religious beliefs." Although it is difficult to make out the text of this letter, Peirce seems to be saying that if the trustees would not sanction his lectures he would give them at his house. No such lectures seem to have been given, though his 13 May paper was probably a preview of what he had in mind. The Club's minute book only reports that "it had special reference to the proofs of the existence of a God," and the June 1884 Circular that it was "on the logic of religious life."
One of the manuscripts from this period (MS 505) is evidently an outline for an oral presentation and it may be the outline for the Metaphysical Club paper. There are no references, however, to existence proofs. It has "reading times" marked at the left margin which indicate that the first three pages took twenty-one minutes. It begins:
"Religion must be subject to good sense. It is always in danger of being carried to excess. . . . Morality cannot be carried to excess. Logic cannot be carried to excess; and it is not subject to good sense, but on the contrary gives good sense its law. But religion if not taken in moderation leads to insanity and that not as is sometimes said, because it is adulterated, but because of the element of it that is most essential,—the mystical element."
A fourth page, perhaps an outline for a separate talk, begins by asserting that "Scientists have faith in science" and "religionists want faith in religion." Peirce then mentions the prayer test which he says, is "also a test of faith." He goes on to say that if religionists really had faith they would not be afraid of science but would encourage it, "sure that it would ultimately be found on their side." Peirce ends with the following outlined remarks, the Cayley references supporting the supposition that they were intended for a talk at the Johns Hopkins:
"Reality. True nature given by me. Opposed to conception which makes it origin of force. True philosophy adequate to govern the science of the XIX Century, develops itself from my conception alone.
"Passage of Cayley's address. 58 Appears at first sight an anachronism. A man like Cayley had better not be rashly accused of anachronism. Really what distinguishes this XIX above all is the force of Ã-.
"How this came about.
"To the businessman—gold alone is real. To the physicist force alone. To the mathematician relations alone; Ã- more real than gold."
Peirce presented his final paper to the Metaphysical Club on 18 November, two and a half months after his appointment had ended. He discussed Petrus Peregrinus's De magnete which he had transcribed from a manuscript in the Bibliothèque Nationale the previous summer and which, because he thought it held a significant place in the history of scientific method, 59 he hoped to publish with an English translation. At the club's fortieth meeting president Hall recommended that it be reconstituted to reflect the reorganization of the Johns Hopkins philosophy program. According to the minute book there were only three more meetings, the last on 3 March 1885. Even in Peirce’s absence, for he did not attend again and had left Baltimore by the new year, his influence continued. On 27 January Jastrow gave a demonstration of logic machines including the Stanhope Demonstrator, Marquand's machine for syllogistic variations, and two machines of his own. At the previous meeting, on 16 December, A. T. Bruce had read a paper on "Final Causes" arguing that "natural selection was a process, not consistent with the notion of a designer but more akin to the action of chance." This suggests the influence of Peirce’s "Design and Chance." At the club's last meeting, M. I. Swift also spoke on "Final Causes."
In the spring of 1884 Hall, now Professor of Psychology and Pedagogy, had organized a program of lectures for about eighty graduate students planning to become teachers, with lectures by President Gilman, Gildersleeve, Remsen, Martin, Hall, Adams, Wood, and Peirce. In Hall's original plan, Peirce was slated to give two lectures, one on "The Observational Element in Mathematics" and another on "The a priori Element in Physics." Although no manuscripts with these titles remain, it is likely that item 80 is the first part of a lecture for Hall's special course.
According to a notice in the May issue of Science Peirce read two papers at the spring meeting of the National Academy of Sciences, one on the study of comparative biography and the other (with Jastrow) on whether there is a minimum perceptible difference of sensation. 60 But it is doubtful that Peirce attended that meeting, and the paper with Jastrow was first read at the October meeting of the Academy and published in its Memoirs (P 303). He read two other papers at the Academy meetings in Newport : "On Gravitation Survey," and "On the Algebra of Logic," the latter probably from what would soon appear in the American Journal of Mathematics (P 296).
It is remarkable that despite what must have been a great tragedy for Peirce—the loss of his academic position (and $2500 salary), the disappointment of having to prepare to leave the home he and his new bride had only a few months before begun to furnish, and the growing awareness that he and Juliette were now personae non gratae, especially in the home of President Gilman—he was able to remain productive as a scholar (and as a scientist).
But such a stunning blow would inevitably affect the course of his work. At first Peirce shifted much of his attention to science and his work for the Coast Survey. In October he had taken charge of the Office of Weights and Measures and had sought to convince Congress of the need for an efficient bureau of standards. And 1885 was largely devoted to pendulum swinging at Key West, Ann Arbor, Madison, and Cornell. But in July the Coast Survey was rocked by scandal; Hilgard was fired and the value of Peirce’s work was impugned. Although Peirce’s reputation was soon restored, the allegation that his work was of "meagre value" had greatly wounded him. When the Survey was placed in the hands of the chief clerk of the Internal Revenue Bureau, F. M. Thorn, who was a lawyer and not a man of science, Peirce knew that his days there were numbered. The enthusiasm that had been rekindled after his dismissal from the Johns Hopkins began to wane.
Another change in Peirce can be traced to his separation from teaching. Although he did not immediately give up the idea of teaching but in June 1885 proposed a course of twelve lectures on advanced logic at Harvard 61 and also developed a correspondence course that he offered for a while, the intense and fruitful interaction he had enjoyed with his logic students at the Johns Hopkins was over. Peirce now had time for the more solitary speculations that would lead to his grand architectonic schemes of the late '80s and '90s ("Guess at the Riddle" and the first Monist series). The most obvious beginning of this new philosophy was his Metaphysical Club lecture on "Design and Chance."
The lecture draws together a number of ideas that had become prominent in Peirce’s writings and lectures. He had long been interested in the Darwinian controversy which had swept America after the first copies of Origin of the Species arrived in the fall of 1859, and as early as the following summer he was convinced that Darwin's theory, "which was nourished by positive observation," was destined to play a major rôle in the development of thought for years to come. 62 Philip Wiener has suggested that Peirce saw in evolutionism, when welded to his "rigorous scientific logic," a way to "make room for freedom of the individual will and religious values," 63and Max Fisch has suggested that "Peirce had an ulterior interest in the logic of evolution as a weapon in his lifelong war against nominalism." 64 But Peirce was also driven by the desire of the scientific philosopher to find things out and to bring whatever he could within the scope of explanatory hypotheses, and he was committed to the economy of explanation—he was a wielder of Ockham's razor—and always sought theories that represented the universe as parsimoniously as its richness would allow. In evolutionism he saw the prospect for a theory he could generalize and develop into a cosmological principle of the highest order.
Perhaps the key Darwinian idea that so attracted Peirce was that of the long run: "Darwin, while unable to say what the operation of variation and natural selection in any individual case will be, demonstrates that in the long run they will adapt animals to their circumstances" (W3:244). But Peirce had made a special study of induction and probability and was well acquainted with sampling techniques and the tendency of random events, when sufficiently multiplied in controlled experiments, to assume as a group a determinate character. His understanding of statistics led him to his view of induction as a self-corrective process. If we add to these ideas his conception of habit as a tendency to act in ways that have not met with (or that have over time met with the least) resistance (the irritation of doubt is a kind of resistance), so that a habit is a statistical result of sorts, then we have most of the ingredients for the bold thesis of "Design and Chance." Perhaps it was the suggestive Epicurean vision of the uncaused swerve of atoms that drew together these conceptions in such an original way. What we find in this paper for the first time is Peirce’s hypothesis that chance is really operative in the universe, even in the realm of laws. 65
His main line of argument is that the fundamental postulate of logic, that everything is explicable, cannot be absolutely true—or at least, that there are good reasons for doubting its absoluteness. One of these reasons is that the operation of absolute chance, which is allowed for if the absoluteness of the postulate is rejected, provides the basis for a theory of cosmic evolution that promises both "the possibility of an indefinite approximation to a complete explanation of nature" and general guidelines for further scientific research. The hypotheses of absolute chance and universal evolution provide the means, perhaps the only means, of satisfying the non-absolute version of the postulate, which asserts that "everything is explicable . . . in a general way." So even though Peirce is challenging the absolute truth of the claim that everything is explicable, his motive is to explain, or to make possible the explanation of, facts which had hitherto remained inexplicable—the laws of nature, similarities among those laws, the general fact that there are laws, and so on and thus, by introducing the hypotheses of absolute chance, habit-taking, and universal evolution, to extend rather than reduce the range of explicability.
The introduction of absolute chance provides for the possibility of an indefinitely close approximation to a complete explanation of nature by allowing for the origin and growth of a tendency to habit-taking. On this view the laws of nature become both "statistical results" and "habits gradually acquired by systems." A kind of natural selection can take place among various systems, according to whether they develop "good" habits, "bad" habits, or no habits. Selection, in the form of elimination, takes place when a system disintegrates and also when entities move beyond the limits of the perceptible universe.
Peirce has generalized Darwinism, since what Darwin had done was to apply the "statistical method" (or probability theory) to the explanation of species, which had commonly been considered absolute and immutable. Peirce applies the same statistical method to the explanation of all regularities, including laws of nature, which still were generally assumed to be absolute and immutable. Add to this the sort of natural selection among habit-systems mentioned above, and the analogy between Darwinism and Peirce’s evolutionism is very strong.
Despite its relative brevity and its incompleteness in the extant manuscript, the argument of "Design and Chance" is sufficiently strong and suggestive to stand as a major statement of Peirce’s evolutionary explanation of the laws of nature—one worthy of close study and comparison with his later, more detailed presentations of the hypothesis. The paper records his rejection of his earlier necessitarianism in favor of tychism, and sets forth significant new developments in his views on the logic of explanation and the problem of induction. It is an important early attempt to advance his view that Nature performs not only deductions, but inductions and retroductions (abductions) as well.
Relieved of the duty to prepare regular lectures, Peirce could now take time to ponder his cosmological speculations. In the coming months his commitment to the Survey would wane, as his methods became less appreciated and his duties became fewer, and he could take even more time for deep reflections. He would soon be ready to make his guess at the riddle of the universe.
NATHAN HOUSER
NOTES
1
I thank Professor Max H. Fisch,
without whose advice and extensive files this introduction could not
have been written. For further information about Peirce’s time in
Baltimore, see his "Peirce at the Johns Hopkins," included in the
invaluable collection of some of his papers: Peirce, Semeiotic, and
Pragmatism, ed. Kenneth L. Ketner and Christian J. W. Kloesel,
(Bloomington: Indiana University Press, 1986); for information about
Peirce’s scientific work, see the published writings of Victor Lenzen
and Carolyn Eisele.
To reduce the number of footnotes, I do not
give references for items that can be easily located by keeping the
following in mind: all manuscript references are to the Peirce Papers at
Harvard University which also contain the correspondence between Peirce
and his parents; Daniel C. Gilman's correspondence, as well as the
Metaphysical Club minute book, is in the Milton S. Eisenhower Library at
the Johns Hopkins University; Allan Marquand's lecture notes are in the
Princeton University Library; all correspondence with employees of the
Coast Survey are in Record Group 23 in the National Archives; Max
Fisch's correspondence is in the Peirce Edition Project in
Indianapolis.
2 See "Reminiscences of Peirce," in Benjamin Peirce 1809-1880; Biographical Sketch and Bibliography, ed. Raymond Clare Archibald (Oberlin, OH: Mathematical Association of America, 1925; reprinted New York: Arno Press, 1980).
3Sketches and Reminiscences of the Radical Club, ed. Mrs. John T. Sargent (Boston: James R. Osgood & Co. 1880), pp. 379-80.
4 Victor Lenzen to Max H. Fisch, 3 March 1963.
5 John W. Servos, "Mathematics and the Physical Sciences in America, 1880-1930," Isis 77 (1986): 611-29. These men had all been students of Benjamin Peirce.
6 Henry James to Henry S. Leonard, 2 Oct. 1936.
7 The Coast Survey became the Coast and Geodetic Survey in 1878, thereby signifying official recognition that geodesy was now the regular business of the Survey. Peirce’s father had played an important r™le in bringing about this expansion of its responsibilities. For conveniences sake, I use the older and shorter name.
8 This extract from Patterson's letter to Sherman, and the extracts referred to therein, are included in Patterson's 8 August 1879 letter to Peirce (L 91).
9 Allegheny was a city in Allegheny County, Pennsylvania, which later amalgamated with Pittsburgh.
10Peirce to J. H. Kehler, 22 June 1911 (L 231).
11 Austria, Denmark, England, Finland, France, Germany, Holland, Norway, Russia, Sweden, and the United States.
12 Peirce to Greely, 27 November 1888 (L 174).
13Quoted in Fisch (1986), p. 129.
14Life of Daniel Coit Gilman (New York: Dodd, Mead & Co., 1910), p. 239.
15 "Charles S. Peirce at the Johns Hopkins," Journal of Philosophy 26 (1916): 716.
16Reported by Cassius J. Keyser in "Charles Sanders Peirce as a Pioneer," Galois Lectures (Scripta Mathematica Library: No. 5, 1941), p. 94.
17 Daniel C. Gilman, The Launching of a University (New York: Dodd, Mead & Co., 1906), p. 66.
18 Fisch (1986), pp. 63-64.
19 Review of "Philosophy in the United States," Mind 4 (1879): 101f.
20 Life and Confessions of a Psychologist (New York: D. Appleton Co., 1923), p. 226.
21 See "The Correspondence with Simon Newcomb," in Studies in the Scientific and Mathematical Philosophy of Charles S. Peirce, ed. R. M. Martin (The Hague, Paris, New York: Mouton Publishers, 1979). For Peirce’s last letter to Newcomb see pp. 86-88.
22 Mind 8 (1883): 594-603.
23 "Charles S. Peirce at the Johns Hopkins," 717.
24 Ibid., 716.
25 Joseph Jastrow, "Charles S. Peirce as a Teacher," Journal of Philosophy 26 (1916): 724-25.
26 "Charles S. Peirce at the Johns Hopkins," 717.
27 Edward L. Youmans, editor of the Popular Science Monthly, where Peirce’s six "Illustrations" appeared, hoped to combine them with additional "Illustrations" in a book for his International Scientific Series.
28 Fisch (1986), pp. 235-37.
29 Johns Hopkins University Circulars 1 (1880): 16.
30 See Arthur N. Prior, "The Algebra of the Copula," in Studies in the Philosophy of Charles Sanders Peirce, 2nd series, ed. Edward C. Moore and Richard S. Robin (Amherst: University of Massachusetts Press, 1964), pp. 79-94; especially pp. 88-92.
31 Alfred Tarski, "On the Calculus of Relations," Journal of Symbolic Logic 6 (1941): 73.
32 V. N. Salii, Lattices with Unique Complements, tr. G. A. Kandall (Providence, RI: American Mathematical Society, 1988), p. vii.
33"Sets of Independent Postulates for the Algebra of Logic," Transactions of the American Mathematical Society 5 (1904): 288-309.
34Survey of Symbolic Logic (Berkeley: University of California Press, 1918).
35 See Salii (1988), pp. 36ff.
36 "A Set of Five Independent Postulates for Boolean Algebras, with application to logical constants," Transactions of the American Mathematical Society 14 (1913): 481-88.
37 The Development of Mathematics, 2nd ed. (New York: McGraw-Hill, 1945), p. 250.
38 See also, however, Mitchell's table on p. 75 of his paper in Studies in Logic ("On a New Algebra of Logic") and Peirce’s table on p. 442 of his principal contribution ("A Theory of Probable Inference," item 64).
39 See Fisch (1986), pp. 52-53.
40 Paul Shields, "Charles S. Peirce on the Logic of Number," Diss. Fordham 1981.
41 Ellery W. Davis, "Charles Peirce at Johns Hopkins," Mid-West Quarterly 2 (1914): 48-56.
42 Studies in Deductive Logic (London: Macmillan, 1880), p. xxiii.
43 "On the various notations adopted for expressing the common propositions of Logic," Proceedings of the Cambridge Philosophical Society 4 (1883): 36-47. Reprinted in Symbolic Logic (London: MacMillan and Co., 1881).
44 Robin MS 302.
45 Nature 25 (1882): 597.
46 Robin MS 431.
47 Johns Hopkins University Circulars1 (1882): 203. Reprinted in James J. Sylvester, Mathematical Papers (Cambridge: University Press, 1909), 3:643.
48 Robin MS 431.
49 Peirce to Carus, 3 March 1893 (L 77).
50 Peirce to Perry, 24 March 1883 (L 344).
51 Semiotics and Significs, ed. Charles S. Hardwick (Bloomington and London: Indiana University Press, 1977), p. 29.
52 Johns Hopkins University Circulars 3 (1884): 119.
53"Charles S. Peirce as a Teacher," 725.
54 "The Longevity of Great Men," Science 8 (1886): 294-96 (also in Nature of 4 Nov. 1886); "Genius and Precocity," Christian Union 37 (1888): 264-66; a related paper with the same title appeared in the Journal of Education (July 1888): 326-28.
55Charles Wilbur de Lyon Nicholls, "Annals of a Remarkable Salon," unpublished brochure, deposited in the Johns Hopkins University Library.
56Newcomb's wife, Mary Hassler Newcomb, was the granddaughter of Ferdinand Hassler, first superintendent of the Coast Survey. She appears to have taken a special interest in finding out the worst about Peirce. See Josiah L. Auspitz, Commentary 52 (1983): 51-64.
57Darnell Rucker, The Chicago Pragmatists (Minneapolis: University of Minnesota Press, 1969), p. 10.
58Peirce may have had the following passage in mind: "I would myself say that the purely imaginary objects are the only realities, the ontwV onta , in regard to which the corresponding physical objects are as the shadows in the cave." The quotation is from the "Inaugural Address by Arthur Cayley," Nature 28 (1883): 492.
59Historical Perspectives on Peirce’s Logic of Science, ed. Carolyn Eisele (Berlin: New York, Amsterdam: Mouton, 1985), 1:4 15-95.
60See also Nature 30 (1884): 40.
61Peirce to James, 20 June 1885 (Wm. James Papers, Harvard University).
62Fisch (1986), p. 23.
63 Philip P. Wiener, "Peirce’s Evolutionary Interpretations of the History of Science," in Studies in the Philosophy of Charles Sanders Peirce, ed. Wiener and Young (Cambridge: Harvard University Press, 1952), p. 143.
64Fisch (1986), p. 29.
65The next four paragraphs are a slight recasting of a summary statement about "Design and Chance" prepared by William Davenport.
Original readings are given in brackets after the correction.
1989 [1986]
383 [385]
1 July ’67 [1 Dec.] line to be moved after l. 17 in Chronology
acquired [acquried]
Measurements [Measurement]
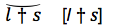
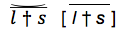
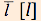
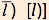
Associative [Asociative]
400.13–20 [400.13–21]
The block quotation excerpted from Peirce’s 1902 application to the Carnegie Institution was taken from a typescript (RL 75C: 611–612) that someone typed for Peirce from a manuscript Peirce had prepared (the last version of many drafts). The typescript contains several errors of transcription, mostly in accidentals. We are listing them below, using the first line of the quotation as line #1. The reading to the left of the bracket restores the manuscript reading (except for entry l. 6, where we italicize the book title Peirce had surrounded with single quotes, rendered as double quotes in W4); the bracketed reading represents the typescript as reproduced in W4: 588. The manuscript text is in RL 75A: 27–30, or equivalently in RL 75: 368–71.
present [general]
logic. [Logic.]
Studies in Logic, [“Studies in Logic,”]
name, [name[,]]
Abduction [abduction]
Induction [induction]
Abduction [abduction]
Induction [induction]
Abduction [abduction]
Subsequently, [Subsequently]
that category [the category]
sea [sea,]
The last line of the block quotation is followed by four more interesting sentences in the paragraph it comes from (RL 75: 30):
My gratitude to the man who will show me where I am wrong in logic will have no bounds. Thus far, I have had to find out for myself as well as I could. Meantime, be it observed that the kind of error which I have been considering can never amount to anything worse than a faulty classification. All that I asserted about probable inference in my Johns Hopkins paper and in my Monist paper was perfectly true.
“We gather what is passing in one another’s minds in large measure from sensations so faint that we are not fairly aware of having them, and can give no account of how we reach our conclusions about such matters.”
Volume 5 of this edition covers the start of an important transition in Peirce’s life. Following his forced resignation from the Johns Hopkins University, Peirce continued to work for the U.S. Coast and Geodetic Survey. His increasing disaffection toward the Survey, however, led to a rekindling of his enthusiasm for speculative philosophy. Volume 5 includes several writings, especially “One, Two, Three,” that convey his growing excitement over the synthesizing and heuristic power of his theory of categories. It is in this volume that Peirce’s extends the categories from thought to nature for the first time and forever, and that firstness, secondness and thirdness are born in both genuine and degenerate forms. Descriptions and arguments in their regard will find their way two years later into Peirce’s 1887–1888 “A Guess at the Riddle” (published in Volume 6).
Many of the writings in Volume 5 are the outcome of work begun by Peirce at Johns Hopkins. Most notable among these are the (unfinished) “Study of Great Men,” which Peirce undertook to test the usefulness of statistical methods for comparative biography; the groundbreaking paper in experimental psychology, “On Small Differences of Sensation,” written with his student Joseph Jastrow; and the 1885 paper “On the Algebra of Logic,” in which Peirce (independently of Frege but inspired by his student Oscar Mitchell) introduced quantification notation and methods, the concept of truth-value, and truth-function analysis for testing theorems. Several writings related to this last paper appear in this volume for the first time, and there are other papers for readers interested in the evolution of Peirce’s logic and the general history of logic.
Also included in Volume 5 are scientific papers that Peirce contributed to the annual reports of the Coast Survey (notably on the flexure of the pendulum, the swaying of the pendulum support, the use of the noddy to measure that swaying, and on the interference between the noddy and the pendulum’s period) and an account of his testimony to Congress about the organization of the Survey.
Perhaps most interesting for the philosopher, besides the groundbreaking papers on the categories, is Peirce’s review of Royce’s Religious Aspect of Philosophy, a review Royce (an “American Plato”) never got to read since it was not published during his lifetime, but which begins to mark both the similarities and the differences between two thinkers who, over ensuing decades, will grow philosophically very close—so close, fortunately, that, had it not been for Royce, Peirce’s papers might have fallen into oblivion.
“It is absurd to speak of choosing an original and ultimate aim. That is something which if you haven’t it, you have nothing to do but wait till the grace of God confers it on you.”
“We gather what is passing in one another’s minds in large measure from sensations so faint that we are not fairly aware of having them, and can give no account of how we reach our conclusions about such matters.”
Volume 5 of this edition covers the start of an important transition in Peirce’s life. Following his forced resignation from the Johns Hopkins University, Peirce continued to work for the U.S. Coast and Geodetic Survey. His increasing disaffection toward the Survey, however, led to a rekindling of his enthusiasm for speculative philosophy. Volume 5 includes several writings, especially “One, Two, Three,” that convey his growing excitement over the synthesizing and heuristic power of his theory of categories. It is in this volume that Peirce’s extends the categories from thought to nature for the first time and forever, and that firstness, secondness and thirdness are born in both genuine and degenerate forms. Descriptions and arguments in their regard will find their way two years later into Peirce’s 1887–1888 “A Guess at the Riddle” (published in Volume 6).
Many of the writings in Volume 5 are the outcome of work begun by Peirce at Johns Hopkins. Most notable among these are the (unfinished) “Study of Great Men,” which Peirce undertook to test the usefulness of statistical methods for comparative biography; the groundbreaking paper in experimental psychology, “On Small Differences of Sensation,” written with his student Joseph Jastrow; and the 1885 paper “On the Algebra of Logic,” in which Peirce (independently of Frege but inspired by his student Oscar Mitchell) introduced quantification notation and methods, the concept of truth-value, and truth-function analysis for testing theorems. Several writings related to this last paper appear in this volume for the first time, and there are other papers for readers interested in the evolution of Peirce’s logic and the general history of logic.
Also included in Volume 5 are scientific papers that Peirce contributed to the annual reports of the Coast Survey (notably on the flexure of the pendulum, the swaying of the pendulum support, the use of the noddy to measure that swaying, and on the interference between the noddy and the pendulum’s period) and an account of his testimony to Congress about the organization of the Survey.
Perhaps most interesting for the philosopher, besides the groundbreaking papers on the categories, is Peirce’s review of Royce’s Religious Aspect of Philosophy, a review Royce (an “American Plato”) never got to read since it was not published during his lifetime, but which begins to mark both the similarities and the differences between two thinkers who, over ensuing decades, will grow philosophically very close—so close, fortunately, that, had it not been for Royce, Peirce’s papers might have fallen into oblivion.
“It is absurd to speak of choosing an original and ultimate aim. That is something which if you haven’t it, you have nothing to do but wait till the grace of God confers it on you.”
|
Preface xi |
The years 1884-1886 were a time of transition for Peirce. When the period began, he intended to make Baltimore his permanent home, confident that his connection with Johns Hopkins was secure. His main work in life would be logic. But he soon learned of the fateful resolution of the Johns Hopkins Executive Committee that his contract would not be renewed, and he knew that his days there were numbered. After his shock had subsided and he had reluctantly yielded to the inevitable, his focus shifted back to his scientific work for the Coast and Geodetic Survey. During these years he probably spent more time on science, either with pendulum observations or with the reduction of scientific data and the preparation of reports, than on all other activities combined. He was on location for the Survey much of the time; almost continuously between July 1884 and February 1886 he directed pendulum operations at a succession of sites extending from Washington, DC to Key West, Florida and Madison, Wisconsin. It might have been a time of passage to a long and influential career in science, but a scandal led to Peirce’s estrangement from the Survey and considerably dampened his enthusiasm for government service. By 1886 his scientific interest shifted from gravity research and metrology to such subjects as the study of color and the history of science, which were outside his sphere of responsibility for the Survey, and after the brief resurgence of his enthusiasm for science, philosophy came again to dominate his thought. 1
These years mark the end of what Max Fisch calls Peirce’s "cosmopolitan period," a time devoted mainly to science and frequent travels in Europe and throughout the United States and Canada. 2 That period began in June 1870, when Peirce sailed for Europe to arrange for scientific observations of the 22 December solar eclipse,3 and ended in April 1887, when he and his second wife, Juliette, moved to Milford, Pennsylvania, a Pocono Mountain resort town. The following year the Peirces settled on a farm on the Delaware River just outside Milford in the home they would soon name "Arisbe," and in the years that followed, except for frequent trips to New York City (some for extended intervals) and occasional trips to Cambridge, Peirce stayed in Pennsylvania.
From a different point of view, that of Peirce’s intellectual growth, the years 1884-1886 mark a new beginning. According to Murray Murphey, this is the start of the fourth and final phase of Peirce’s intellectual development, stemming from his discovery of quantification and set theory.4 In 1883 Peirce’s Johns Hopkins student Oscar Howard Mitchell had introduced indices into algebraic logic in a way Peirce recognized as the key to quantification.5 Over the following months (see items 20-22), Peirce developed a theory of quantification that by 1885 (items 30-32) took a very modern form. At about the same time, he first came into contact with the work of Georg Cantor (see MS 530), which must have been a stimulus for the investigations he had already begun on number theory. He had probably also begun to reflect deeply on the nature of continuity, for by 1 April 1884, while working on the definition for the Century Dictionary, he lamented that "continuity" had never been adequately defined: "Kant's definition, to which I am ashamed to say I have hitherto given my adhesion, is ridiculous when you come to think of it" (MS 528).6 By that time Peirce had begun to formulate his unique theory of the continuum that would ground his anti-Cantorian set theory (and theory of number). His discovery of the quantifier and set theory marks the beginning of a major phase of his intellectual development because, as Murphey has shown, Peirce was forced to make major revisions to his theory of reality and to his categories. 7 The groundwork for this final period in Peirce’s thought was laid in works included in the present volume.
Peirce wrote or published over one hundred papers and reports between 1884 and 1886, ranging in subject matter from the measurement of sensations and the price of sugar to the algebra of logic and philosophical categories. Most of the fifty-eight items included in the present volume belong to science, logic, or philosophy; the Study of Great Men, which fills eighty pages (items 2-19), was described by Peirce as comparative biography, and thirty-two pages (item 57) are devoted to definitions of words beginning with the letter "e" that Peirce drafted for the Century Dictionary. At least one paper (item 24) belongs most appropriately with psychology, and there are four private letters and several reviews.
For much of this three-year period the Peirces were
itinerant. They stayed in Baltimore for the first
half of 1884, where Peirce’s contract with Johns Hopkins
ran until September, but spent the summer in Virginia,
where Peirce was conducting gravity experiments and
looking for sites for new pendulum stations. They
were in Washington for much of the latter part of 1884
and the first part of 1885, where from October to February
Peirce was in charge of the Office of Weights and Measures
and directed pendulum operations at the Smithsonian.
From March 1885 through February 1886 the Peirces
traveled for extended visits to Key West, Ann Arbor,
Madison, and Ithaca, all on Coast Survey business.
Finally in 1886, engaged only in local operations
and soon to be relieved of fieldwork so that he could
devote his time to preparing reports, he settled down
in New York City, where he and Juliette stayed until
their move to Pennsylvania the following year.
The year 1884 may have been the worst of Peirce’s life (although Joseph Brent's biography reveals that there were bitter years still ahead). Peirce and Juliette had been married for only a few months and had hardly settled into their newly leased house when they learned of the decision by the Johns Hopkins trustees to let Peirce go.8 It is clear now—though it was not then—that Peirce’s dismissal was a sign that society could not tolerate his disregard for its conventions. His unique and somewhat arrogant individuality was too much at odds with the tenor of the times, and especially the conservatism of Baltimore. (Ironically, in less than a decade Peirce would express grave reservations about the American propensity to regard one's character as an individual as more important than one's social character.) By mid-year Peirce and Juliette knew that they would have to give up their Baltimore house and dispose of the elegant home furnishings they had so painstakingly chosen. The shock and disappointment of this turn of events led to ill-health and despair. 9
It must have come as a relief when in July 1884 Peirce was assigned to Fort Monroe in Virginia to make gravity determinations, and then to reconnoiter for one or two more stations in the mountains of the Virginias and North Carolina. Traveling with Juliette, Peirce arrived at Fort Monroe at the bottom of Chesapeake Bay on 23 July and proceeded to set up a station. The Superintendent's Report for the fiscal year ending June 1885 (P 331) indicates that only Peirce Pendulum No. 3 was swung and that Peirce was pleased with the results. In addition to gravity measurements, Peirce experimented with the use of an instrument, called a noddy, for measuring the swaying of the pendulum support and worked up some theoretical results for the 1884 Report (item 42). In September Peirce looked for new mountain stations, but not finding any that met the Superintendent's specifications, he returned to Washington toward the end of the month and on 1 October was put in charge of the Office of Weights and Measures, an agency of the Coast Survey.
Peirce began his tenure with a great deal of energy and enthusiasm and even announced to Superintendent Julius Hilgard that he would write a book on the history of standards. Before year's end he had traveled to Boston, Providence, Hartford, New York, and Philadelphia and had met with electricians and manufacturers of gauges and other machinery in order to determine how best to meet the need for metrical standards as recommended by the U.S. Electrical Conference. In mid-October he attended the scientific session of the National Academy of Sciences in Newport, where he presented three papers: "On Gravitation Survey" (P 281), "On Minimum Differences of Sensibility," co-authored with Joseph Jastrow (P 282), and "On the Algebra of Logic" (P 283). His paper on logic must have been a preview, along the lines of items 20-22, of the paper he would soon finish for the American Journal of Mathematics (item 30). The paper on gravity surveys elaborated on a program for future gravity determinations that Peirce had proposed to Hilgard in his 1 October letter (item 23) and that was summarized in the 24 October issue of Science (pp. 396-97):
Mr. C. S. Peirce explained some of the errors still needing correction in Pendulum observations, particularly such as were due to the flexure of the pendulum. He presented the outline of a scheme for a gravitation survey of the entire country, indicating the position of points in the eastern portion of the country which he thought most desirable to occupy, in which the stations would be about two hundred miles apart, regions of geological disturbance avoided, but their sides occupied, together with the summits of the higher mountains. Seven or eight stations could be occupied in a year, and thus a series of curves secured which would give us the form of the geoid; i.e., of the surface beneath the continent where the force of gravity was uniform.
While in Newport he took time to investigate an old stone mill to try to determine what standard of length had been used for its construction, probably thinking that he might help settle a dispute about the mill's origin. He argued that the construction of such a building would have required a "drawing to scale" and therefore a unit of length, which he assumed was either the English or Norse foot. In December he published his findings in Science (item 26) and might have established himself in the popular mind as an authority in the field of measurement—but alas, his conclusions favored a Norse origin for the mill and it was soon revealed that it was English (which fact had already appeared in print).10 In fairness to Peirce it must be said that he stated his purpose as purely metrological and that he had deliberately declined to offer an archeological opinion.
On 30 December 1884 Peirce attended the meeting of the American Metrological Society at Columbia College in New York City. He read a paper on the determination of gravity (P 270) and gave an account of his measures of the Old Stone Mill. He also participated in a discussion of the adequacy of the standards of weight and measure in the United States and pointed out some of the deficiencies in the current system. As a result of his revelations, the Society passed a resolution recommending the appointment of a committee to advise Congress on the need for establishing an efficient bureau of standards.
Peirce had managed to finish this difficult year with a burst of energy. Perhaps he had resigned himself to a non-academic life and had readjusted to the idea of a life of science. Toward the end of the year, he began a series of five lengthy occupations that would continue to the end of January 1886, at stations in Washington, Key West, Ann Arbor, Madison, and Ithaca. The occupations began at the Smithsonian, where all four Peirce Pendulums were measured (compared to standards) in preparation for the elaborate fieldwork ahead, and continued there under his direction through February 1885.
Probably the most important of Peirce’s scientific writings to appear in print in 1884 was his "Determinations of Gravity at Allegheny, Ebensburgh, and York, Pa., in 1879 and 1880" (item 1). It had been scheduled to appear in two previous Coast Survey Reports, but he had not been able to finish it because he was overextended with his dual appointment at Johns Hopkins. It is an important work, in part because it connects American geodetic methods and results with European geodesy. Another 1884 publication, Observations with the Meridian Photometer During the Years 1879-1882 (P 271), makes heavy use of Peirce’s scientific findings, in particular his Photometric Researches (P 118).
When his Johns Hopkins classes ended in the spring of 1884, Peirce might have stopped his university related research, but a momentum had built up that carried him along for several months. In the fall of 1883 he had begun teaching a course on the psychology of great men, a subject he had found interesting since boyhood. As early as 1860, in his "Private Thoughts," he had reflected on greatness and had concluded that a great man should be revered "notwithstanding his mistakes" (W1:5). The subject of human character was a topic of general interest and was addressed on more than one occasion at the Johns Hopkins Metaphysical Club: the work of Francis Galton was discussed on at least two occasions, and William James's "Great Men, Great Thoughts, and the Environment" was the topic for one meeting. A special interest of Peirce while at Johns Hopkins was the application of statistics to different subjects, and comparative biography lent itself to the illustration of statistical investigations that depended largely on impressionistic data. Some years later Peirce wrote that he had "cast about for a subject that might afford valuable training in such inductive investigation [as] the members of my class might need in future life and which they would not be likely to acquire in their other classes" (CP 7.256). The course, although poorly enrolled (like many of Peirce’s other courses), was an apparent success. A carefully thought out program was followed that involved reading standard biographies and extracting relevant information (the question of relevance having been settled beforehand), compiling impressionistic lists of great men (and a few women), and submitting the resulting data to statistical examination. The study was carried on informally by Peirce and his students after the course had ended, apparently up to the time of his final departure from Baltimore near the end of 1884. In the absence of a complete record of the research it is unclear how far the study had progressed by then, and it seems likely that results were spread among the papers of the participants. The parts that are published here (items 2-19) give only a sampling of the methods and results as preserved in pages that remain with the Peirce Papers, and it may appear that the study never achieved any considerable success. But later discussions in Peirce’s writings11and references to the study made by Jastrow suggest otherwise. When in 1894 the American educator Albert Yoder asked G. Stanley Hall, then of Clark University, about the study of greatness, Hall referred him to Peirce. Some years after he had left Baltimore, possibly stimulated by the 1891 publication of The Man of Genius by Cesare Lombroso and the 1892 New Calendar of Great Men (based on Comte's positivist calendar),12 Peirce’s interest in the old study was rekindled. An invitation to give the 1892 Lowell Lectures led Peirce to write to Augustus Lowell suggesting his "Comparative Biography of Great Men" as a topic for the series:
It refers, not to the eminent men whom Galton has studied, but to a higher order, the phenomena of the history of mankind. A list of about 300 of such men would be formed and discussed and a method for the comparative study of them developed. Comparative lives of a few of them would be given,—a sort of scientific Plutarch,—scientific I mean in the treatment, not so exclusively as to the subjects. Finally, a large number of general questions relating to the nature, kinds, causes, and characters of greatness would be inductively considered. 13
Peirce took up the study again at the turn of the century and in 1901 published a paper on "The Century's Great Men of Science." In a manuscript related to that paper (Harvard MS 1125), Peirce explained more fully his distinction between eminent men and truly great men:
the native capacity of the lesser great men, like that of the merely eminent men, is due to the accidental coöperation of a thousand minute independent causes such as operate one way or another upon all of us, while the greater ones do somewhat partake of the nature of monstrous births in that their exceptional natures are largely due to causes that very rarely operate at all.
When Peirce recalled the original course of study, it was always with the greatest fondness for his students: "It was one of those matchless classes—the very salt of the earth,—which it was my privilege to enjoy in Baltimore."
Peirce taught two courses in the spring of 1884: one was the second half of his advanced logic course and the other a course on probabilities. His last two advanced logic students were Henry Taber and Joseph Jastrow. Taber had planned to write his dissertation on logic but after Peirce’s dismissal had to give it up because, as he explained in a letter to Paul Weiss dated 3 September 1931, Peirce’s successor "was quite ignorant of formal logic except the very rud[i]ments." Taber held Peirce in high esteem: "I have been told that James, or perhaps it was Royce, I have forgotten which, had said that Peirce impressed him as potentially the most powerful intellect he had ever known. I would certainly subscribe to this estimate of Peirce’s powers."
Peirce’s other advanced student, Jastrow, went on to become a respected psychologist and a well-known debunker of the paranormal.14 In addition to logic (and probability theory—both Jastrow and Taber took the course on probabilities along with five other students, including William E. Story), Jastrow studied experimental psychology independently with Peirce. In his 1930 autobiography Jastrow said that "it was Charles S. Peirce, one of the most exceptional minds that America has produced, who stimulated me most directly." 15 Peirce suggested to Jastrow that they undertake an experiment to test Fechner's claim that human sensations are subject to a limitation he called a Differenzschwelle (the minimum perceptible difference of sensation). Below this threshold it was said to be impossible to discern differences of intensity. Peirce and Jastrow conducted elaborate experiments between 10 December 1883 and 7 April 1884 that constituted the first psychological investigation undertaken at Johns Hopkins and one of the earliest studies in experimental psychology in North America. 16 Peirce described the experiment in a letter to Simon Newcomb dated 7 January 1908:
I note that you ac[c]ept as established the dictum of Gustav Theodor Fechner that the least sensible ratio of light is 101/100. If you will look in volume III Mem. of the U. S. Nat. Acad. of Sci. you will find a paper by me and my then student in logic Joseph Jastrow devoted to the question whether there is or is not such a thing as a "Differenz-Schwelle" or least perceptible difference of sensation.... [We] began with sensations of pressure and for a reason I will shortly mention we ended there. At once, using such precautions as any astronomer would use in observing faint nebulas, without any practice we found that if there were any least perceptible ratio of pressure, it was twenty or thirty times nearer unity than the psychologists had made it to be. We afterward tried to do the same thing for light; but were stopped by the utter impossibility of getting a piece of Bristol board containing a square inch of uniform luminosity. No doubt this might have been overcome. But Jastrow and I were severally pressed with other work and we dropped the investigation—contenting ourselves with what we had done.17
They had good reason to be content. Their report (item 24), presented to the National Academy of Sciences on 17 October 1884 and published in the Academy's Memoirs in 1885, is described by Stephen M. Stigler as unexcelled in the nineteenth century and "a good example of a well-planned and well-documented experiment today.". 18 Stigler points out that the study was the first to employ a "precise, mathematically sound randomization scheme," and also the first to require subjects to state their confidence in their choice (weight A is lighter or heavier than weight B) and to choose even when the level of confidence was zero. Ian Hacking, who also discusses the experiment, points out that Peirce’s understanding of the importance of randomization was at least three decades ahead of his time. 19 Yet Peirce’s idea was forcefully rejected by E. B. Titchener for being out of touch with psychological reality, and it was not reintroduced until R. A. Fisher's Design of Experiments appeared in 1935.20 Hacking also remarks on the interesting last paragraph of item 24 where Peirce and Jastrow indicate that their conclusion has important bearings on such questions as women's insight and telepathic phenomena. The word "telepathy" was less than two years old, according to Hacking. It is noteworthy that at about this time the American Society for Psychical Research was being formed (an organizational meeting was held in Boston on 23 September) to "ascertain the truth in regard to the alleged psychical phenomena" and to expose "charlatan spiritualism." 21
In addition to his gravimetric work, his Johns Hopkins classes and the study of great men, and his work with Jastrow, as well as other activities not yet considered, Peirce somehow managed to devote very productive time in 1884 to algebraic logic. In his 1880 paper in the American Journal of Mathematics (W4: item 19) he had given the first definitions of logical addition and multiplication suitable for modern Boolian algebra and, as Arthur Prior has shown, the system developed in that paper, with only slight enhancements, gives a complete basis for the classical propositional calculus. 22 The paper was intended as the first part of a much longer work on formal logic, but, though Peirce started several continuations (see items 20-22), certain difficulties and discoveries held him back. The greatest difficulty concerned the problem of distribution, which had arisen as a result of his claim that he could easily prove the law of distribution but had omitted a proof because it was too tedious. Ernst Schröder rejoined that Peirce must be mistaken because the independence of one of the distribution principles could be demonstrated—thus showing that the full law could not be proved. Peirce was convinced at first that Schröder was right but later reasserted that distribution could indeed be proved for his system. His position is often said to amount to the claim that every lattice is distributive, but that is almost certainly a misconstrual of Peirce’s views.23
Between 1880 and 1885 Peirce developed a conception of truth values (a sentence has the value v if it is true or f if it is false) and created a semantics for his algebraic logic. Items 20-22 show him in the process of discovery. Stimulated no doubt by Schröder's 1883 paper to the British Association for the Advancement of Science, which argued against Peirce’s distribution claim, but also by his 1882 edition of his father's Linear Associative Algebra and the recent publication of Studies in Logic, Peirce filled these short manuscripts with brilliant flashes of insight. In addition to the systematic introduction of truth values, we find an early statement of truth-function analysis ("it is clear that the truth of a general formula may be tested by trying whether it will always hold when either v or f is substituted throughout for each letter" [p. 112]), the development of quantifiers (following their anticipation in W4: item 66) and remarks about their significance for distinguishing logic from mathematics, the groundwork for "Peirce’s law", matrix representations of universes of discourse, the idea that the elementary logical operations are insertion and deletion (item 20), and a great deal more. The idea that the copula of inclusion might be abandoned in favor of disjunction and conjunction with rules only for insertion (amplification) and deletion (simplification), an idea Peirce got from Mitchell, may be seen as the forerunner of the idea on which Gentzen based his system of natural deduction.24 As late as the summer of 1884 Peirce was still working on a continuation of his 1880 paper, but within a few months he would be ready to relegate reference to the earlier paper to a footnote in what would become his most influential work on logic.
Peirce had delivered his (and Jastrow's) paper on minimum sensibility to the National Academy in October. The success of that study may have encouraged him in his use of statistical methods, for it was soon followed by a paper on the "Success of Predictions" (item 25) in which, according to Stigler, he derived "a latent structure measure of association for 2 X 2 tables."25 In this work Peirce addresses the question whether meteorologists could successfully predict tornadoes. He finished the year with a discussion in the pages of the New York Evening Post and the Nation on the economics of the sugar trade with Cuba (items 27-28).
The year 1884 had been difficult, but by its end Peirce had reoriented himself to a life of science. He was ready to start the Smithsonian occupation, the beginning of more than a year mostly on location—away from Baltimore! And he had his definitions to write for the Century Dictionary, something he had been working on for over a year. Perhaps the worst was over.
By a cruel turn of events, Peirce had hardly settled himself to the harsh reality of his dismissal from Johns Hopkins when he had to face a whole new episode of bitter and painful events. It began without much fanfare as a broad investigation of four federal scientific agencies which had outgrown their original charters: the Geological Survey, the Coast and Geodetic Survey, the Signal Service of the U.S. Army, and the Hydrographic Office of the U.S. Navy. The investigation was conducted by a joint commission of the U.S. Senate under the chairmanship of Senator William B. Allison of Iowa and was undertaken to examine the structure and operation of the four agencies for economy, efficiency, legality, and utility.26 The Commission heard testimony from more than fifty federal employees between 4 December 1884 and 28 February 1885 and in a subsequent session about a year later. Peirce was called to testify on 24 January, one of only ten Survey employees questioned by the Commission. Even though he had been in charge of the Gravimetric Survey for many years, he was questioned almost exclusively about the work of the Office of Weights and Measures, which he had directed only since October 1884. This may have had something to do with the 30 December 1884 resolution of the American Metrological Society, for the Commission's questioning and Peirce’s testimony (item 29) bear a marked resemblance to the discussion at Columbia one month earlier. Peirce made it plain that many, if not most, of the standards in the United States were in great need of improvement. One example that caught the interest of the commissioners was that the hollow brass weights used to weigh out gold for coins minted at Philadelphia and Denver actually measured out different amounts of gold because of the buoyancy of air. The result was that coins minted at Denver contained too much gold. Peirce’s testimony before the Allison Commission and the resolution of the American Metrological Society were the first two steps toward the creation of the National Bureau of Standards.27
In the course of about four months as head of the Office of Weights and Measures Peirce had established a noticeable momentum toward an improved agency. He had written to Superintendent Hilgard on 27 September with an impressive plan for his first six months of service, including the preparation of at least five reports on metrological research (including his long-awaited report on the spectrum meter), some new computations and comparisons, an inventory of instruments and records, the commencement of an index of results, the preparation of a history of instruments and standards, and the systematic collection of foreign publications on metrology for the library. Given Peirce’s obvious enthusiasm, it is surprising that on 22 February 1885, less than five months after his appointment, Peirce declined further service as head of Weights and Measures. The reason for his action was revealed to Simon Newcomb in a letter dated 10 June 1899: "[I] only left because [Hilgard's] physical condition was such as to cause me embarrassment which I thought required me to quit Washington." 28 Hilgard's condition would soon be revealed to the world.
It is not clear whether the findings of the Allison Commission directly damaged Peirce or the Coast Survey, but the mere fact that the investigation was conducted revealed that federal science in America was entering a new age, a time when the value of work would be judged by its immediate practical (economic) benefits. When Grover Cleveland took office in March as the 22nd president of the United States, and his Democratic Party took control of the government, anti-scientific sentiment had won the day. Dedicated to reducing the federal bureaucracy, Cleveland found a ready target in the Coast Survey.29
On 25 July 1885 the Washington Post broke a story with the headline, "Exhorbitant [sic] Expenditures. Coast Survey Officials Suffer Penalty for Extravagance. Superintendent Hilgard Suspended, Several Subordinates Dismissed and an Investigating Committee Appointed." The Post announced that the Treasury Department had for some time been dissatisfied with the Coast Survey accounts and, after an audit, had found them to be "entirely unsatisfactory." Cleveland had dismissed Hilgard and had appointed Frank M. Thorn, chief clerk of the Internal Revenue Bureau, to head a commission to take charge of the Coast Survey office and to conduct a full investigation. On 7 August the Post reported that "the actual condition of the office of [the] survey was one of demoralization, and its workings [were] inefficient, unjust, and to some extent disreputable." Hilgard was accused of misappropriating federal funds and was reported to be an alcoholic, which was widely known and probably contributed to the decision of the Treasury Department to investigate the Survey.30 In a paragraph dealing with Peirce, it was reported that for several years he had been performing pendulum experiments "without restriction or limitation" and that the "meager value" of his work was substantially destroyed by its cost. Peirce was shocked and indignant. He wrote a letter of protest and rebuttal from Ann Arbor on 10 August that was published four days later in the New York Evening Post (P 300) and later in Science (P 317). His chief concern, the main reason for his indignation, was that unscientific men had been permitted to judge the importance of his work and had judged it to be of "meager value." 31 He announced that he would resign if that estimate was accepted by the Survey. It is to Peirce’s credit that the scientific community, even within the Survey, immediately came to his defense. Charles A. Schott wrote to Benjamin A. Colonna: "I trust you will be able to induce Mr P. to reconsider his action and for the sake of the scientific reputation of the Survey, continue the work, now that we are on the eve of reaping the practical benefit of his researches." And at the 28 August 1885 executive meeting of the American Association for the Advancement of Science a resolution was passed on Peirce’s behalf which chastised the Treasury Department for referring the question of the value of scientific work to non-scientists. The Association recognized that an ominous note had been sounded by the Cleveland administration and perhaps foresaw that the shift of power from scientists to bureaucrats would bring about a period of decline for pure science in America. Its resolution urged that the head of the Coast Survey "should be appointed by the President, with the advice and consent of the Senate," and "should have the highest possible standing among scientific men and should command their entire confidence." Peirce’s scientific reputation had been vindicated. Still the scandal was a great strain on him. In October he wrote to William James that
This horrid & sickening business of the Survey makes me long intensely for University life. The villainous things which I hear whispered, the Vandal methods of trying to set things right, the accusations of which I have myself been the subject, combine to make me loathe the Survey so, that I would rather keep a pea-nut stand than stay in it one minute longer than my duty requires me to do.
About six months later, the Allison Commission found that the Geological Survey, headed by John W. Powell, was extravagant in its operations and sought passage of a congressional bill to restrict its work and limit its publications. Again the scientific community was outraged and none more than Peirce. He wrote to Powell assuring him of strong support within the Coast Survey and proposed a plan of attack: "Let the congressmen hear of science, no longer as merely giving reasons, but as an interest, saying We want so and so.... There are a hundred votes in the house to be commanded in this way."32
Tumultuous though it was, 1885 was one of Peirce’s most productive years in the field. On 1 March, after concluding the Smithsonian occupation and within a few days of his resignation from Weights and Measures, Peirce left for Key West. He set up a station in an Army barracks which he occupied until 1 May. Using only Peirce Pendulum No. 2, he discovered that the residual difference between gravity in Washington and Key West was smaller than he had expected. From the Superintendent's Report on Peirce’s work for the year ending June 1885, it appears that the Key West results helped determine his next major assignment.
Referring to the fact that the residual difference of gravity between Washington and Key West is somewhat smaller than he had anticipated, Mr. Peirce expresses the opinion that the question to which gravity research should be directed more particularly for the present is, whether lines of equal residual gravity can be traced upon the map, or whether the merely local variations will mask those that are progressive, and that for this purpose lines of stations a thousand miles or so in length should be run with stations three degrees apart.... The first endeavor should therefore be to run an east and west line.
By this time Peirce should have been able to replace the somewhat defective American-made set of (Peirce) pendulums that he had designed a few years earlier. He had ordered new pendulums from Gautier in Paris during his final European assignment in 1883 but had been directed by Hilgard to return to Washington before they were finished. As a result of a series of inadvertencies, including possibly some disingenuousness on the part of Gautier, communications broke down between the Coast Survey and the Paris manufacturer—and it became a matter of some dispute who if anyone was at fault. As it turned out, the Gautier pendulums were never acquired, and this became the cause of both regret and embitterment for Peirce.33
In July Peirce was directed to make a reconnaissance for an east-west line of three or four stations approximately along the forty-third parallel and as far west as the Mississippi River. Peirce chose Ann Arbor, Madison, and Ithaca and, in August, began operations in Ann Arbor. The American Association for the Advancement of Science held meetings in Ann Arbor while Peirce was stationed there, and it was then that the executive committee passed its resolution of support for him. Operations at the University of Wisconsin began early in October and continued throughout the month. The station was set up in Library Hall (today called Music Hall), which had a clock connected to the University's Washburn Observatory. Peirce’s main contact at the University was Edward S. Holden, Director of the Observatory, with whom he became very friendly (and with whom he would correspond for many years). From Madison Peirce proceeded to Ithaca, where work began by early December. En route the Peirces passed through Niagara Falls, where because of a miscalculation on Peirce’s part, compounded by the delay of a payment from Washington, they were "stranded" for fifteen days. Being stranded in Niagara was not altogether a bad thing, as is revealed in a letter to Holden dated 8 January 1885: "Mrs. Peirce doesn't progress very fast. We stayed a fortnight in Niagara & that did her ever so much good." Peirce spent some of that time working on mathematical problems related to "the effect of the air on the period of the pendulum" (Peirce to Thorn, 7 November 1885), a problem in hydrodynamics that had never been satisfactorily treated. He was impressed with the Falls and frequently referred to it in illustrations in subsequent writings (see especially item 54). Peirce arrived in Ithaca on 19 November 1885, where he found his foreman demoralized because of the delay. By the end of the month Peirce had discharged the man and had hired a Cornell graduate student to replace him. Peirce’s host at Cornell was E. A. Fuertes, Dean of the Faculty of Engineering, who so greatly impressed Peirce that he worked behind the scenes to get him appointed as superintendent of the Survey. Operations in Ithaca continued to the end of January.
At each of these stations, and then again at the Smithsonian, Peirce swung Peirce Pendulums Nos. 2 and 3 (a meter and yard respectively). A description of the procedures employed for these operations appeared in the 1886 Report, which illustrates the laboriousness of gravity determinations (for which the data were hand-recorded for subsequent manual reduction and computation).
Two new pendulum stands had been constructed of improved design, so that two pendulums could be oscillated simultaneously on two supports. Each swinging consisted of five thousand oscillations with heavy end up and fifteen thousand with heavy end down, except that one-fourth of the swingings in the latter position were of double length. There were thus about six hundred thousand oscillations with heavy end down and one hundred and sixty thousand with heavy end up at each station.
The paper that resulted from this series of occupations was Peirce’s second major memoir on gravity—the first was his "Measurements of Gravity at Initial Stations in America and Europe" (P 161; W4: item 13)—and, according to Victor Lenzen, would have been an influential work in geodesy had it appeared in 1890 when Peirce finally had it ready for publication.34 But on the advice of Newcomb, then Superintendent of the Coast Survey Thomas C. Mendenhall declined to print Peirce’s memoir (P 285) and, having decided that Peirce’s usefulness to the Survey had come to an end, asked for his resignation.
Two papers appeared in 1885 as appendices to the 1884 Coast Survey Report and both deal with Peirce’s investigations of the flexure of pendulum stands. "On the Use of the Noddy" (item 42) describes a method he devised for measuring flexure, and "Note on the Effect of a Pendulum upon its Period of Oscillation" (item 43) discusses the degree of disturbance caused by flexure, an effect which he concluded must be considerable "for all the reversible pendulums which have ever been constructed." In the second paper Peirce introduced the expression "kinetic potency" to avoid using the more standard expression "potential energy," which he said "grates upon the ear of a student of Aristotelian philosophy."
Except for his scientific work and the Coast Survey scandal, logic dominated Peirce’s life, at least until August. As a result of the stimulating insights of the summer of 1884 and the realization that he had moved too far from his 1880 paper (W4: item 19) to write a second part, he refocused his attention on a new formalization of logic, self-consciously motivated by his notational discoveries. In the new paper, "Algebra of Logic: A Contribution to the Philosophy of Notation" (item 30), Peirce considered the different kinds of signs necessary for a fully adequate logic system, and he concluded that it is necessary to have tokens (conventional or general signs, usually called symbols), indexes (demonstrative signs), and icons (signs of resemblance). This is the first published application of his revised theory of signs to algebraic logic, which he had begun to formulate in item 22. 35
It is in this paper, appearing February 1885, that Peirce introduces truth-values in giving his decision procedure for theoremhood, and the first theorem proved by that method is his fourth icon, (((p—< q) —<p) —< p), which marks the difference between classical and positive logic.36 The axioms for first-order logic are given in the first five icons, although the fourth (the negation principle) can be used to reduce Peirce’s basis to the Tarski-Bernays axiomatic system for implicational logic.37 Here quantifiers are first introduced in their standard form and Peirce anticipates the modern distinction between first- and second-order logic. 38 Furthermore, he provides the basis for a complete quantification theory with identity 39 and in his discussion of procedures for working with his calculus shows remarkable insight into modern methods, even introducing something very much resembling what today is called Skolem normal form. The paper was widely read and had considerable influence on the development of symbolic logic. It is cited as a key work by many notable logicians, including Peano, Whitehead, Lewis, and Tarski; and through Schröder, Peirce’s most influential follower, its results reached many others, including Löwenheim and Skolem. Lukasiewicz often quoted the first paragraph of Part II to show that Peirce was a precursor in conceiving of many-valued logics.40 Even Bertrand Russell read the paper (along with the 1880 paper) at the turn of the century,41 but how much he was influenced by Peirce, directly or indirectly, is far from clear. In addition to its place in the history of exact logic, for which it is justly acclaimed, item 30 represents an advance in semiotic theory and an important stage in Peirce’s systematic thought.42
Throughout the early months of 1885 and into the summer, Peirce worked on a continuation of item 30, which he justly believed set the stage for a whole new era in logic. On 25 June he wrote to William James: "I have not sent out any copies of my new memoir ... because the paper is not yet completed & the most important part of it is to come. But I consider it as the beginning of a new life for Formal Logic." When he had finished the second part, which extended his theory of quantification and what he called his general algebra of logic, he submitted it to Newcomb, then editor of the American Journal of Mathematics. (J. J. Sylvester, who had agreed in principle to publish it, had returned to England to take up a chair at Oxford.) Newcomb read Peirce’s paper and agreed to publish it only if Peirce said that it was mathematics, not logic. Peirce refused and the paper was rejected.43 He retold this incident to James in August 1905 and, as he often did, gave him a lesson in logic at the same time. In explaining how to draw certain inferences in his general algebra of logic, he made use of the principle [Pi]xlxx —-< [Pi]x[Sigma]ylxy, which led him to reflect:
I do not know whether I ever stated this in print or not. It is a part of a principle thoroughly developed by me in a memoir which Newcomb practically refused to print in 1885 or 1886 which is the reason why I have never since printed anything on logic which could not be put in popular form. I there called the principle (of which this is a very small part) the principle of identification and diversification. It holds good strictly even if there is no x. From "every phenix would burn itself" it follows that "every phenix would burn something." It is somewhat remarkable since [Pi]xlx does not warrant [Sigma]xlx. 44
Item 31 appears to be part of the paper Newcomb rejected. Together with the related item 32—logical investigations carried out over a six-day stretch in May—it represents logic in its most advanced state until after the turn of the century.
Except for logic and the revision of his theory of signs, Peirce had not wrestled with philosophy for over a year—since his lecture on design and chance. But sometime during the summer of 1885 he turned again to speculative philosophy. Several events and circumstances stand out as instrumental in Peirce’s return to philosophy at that time. There was the Coast Survey scandal that thoroughly demoralized him and destroyed his commitment to federal service and a life of experimental science, and there was Newcomb's rejection of his pioneering logic paper, which dampened his enthusiasm for that most formal and technical branch of philosophy. These two events led Peirce to close off avenues he might otherwise have followed, which helped clear the way for his resumption of speculative philosophy. His travels to Michigan, Wisconsin, and Cornell may also have played a part; perhaps someone at one of the universities re-ignited his enthusiasm for philosophy, or perhaps Peirce deliberately turned to philosophy as the field most likely to secure him a teaching position. Brent speculates that Peirce may have had something like that in mind,45and certainly it is clear that he wanted a university post. He had written to James in June about giving a fall course at Harvard, and in October he wrote to his brother James Mills (usually called Jem) that teaching was the life he desired. He knew from his experience at Johns Hopkins (and with Newcomb) that logic was not very marketable, and may therefore have decided to recast his academic profile in the direction of traditional philosophy.
Possibly all these factors played a part in Peirce’s shift of focus back to philosophy in the summer of 1885, but probably the most influential event was the publication of Josiah Royce's Religious Aspect of Philosophy, which appeared mid-year. In his book Royce argued for the existence of God from the possibility of error and, almost as a challenge to Peirce, defended his position against the "modern Thrasymachus" who held that all we can conclude from the possibility of error is the possibility of God. Peirce recognized himself as the modern Thrasymachus and took up the challenge—and in doing so, according to Fisch, "turns some of the will-bes of his Popular Science Monthly series into would-bes, and thereby takes a short step from his earlier nominalistic pragmatism toward his later realistic pragmaticism."46 Peirce wrote a long review (item 33) for Edward L. Youmans's Popular Science Monthly, but, as he explained to William James in a letter of 28 October, it was never printed: "I wrote to Youmans,—at his particular request,—a notice of Royce's book. I was a long time over the book & wrote I thought something really very good, for me; but Youmans wouldn't print it, i.e. he made such a wry mouth that I relieved him of it." In the review, Peirce criticized Royce's idealism as being too much like that of Hegel, whose "capital error ... which permeates his whole system in every part of it is that he almost altogether ignores the Outward Clash." Peirce repeated the thesis of item 30, that three kinds of signs are indispensable in all reasoning, and emphasized the necessity for indexes to refer to individuals: "one such index must enter into every proposition, its function being to designate the subject of discourse." There is no doubt that Royce's book, in conjunction with his own recent discoveries in logic and his revised theory of signs, had a profound effect on Peirce. It was then that Peirce returned to his categories and to a reassessment of Kant.
In an unfinished draft of the review (MS 540), Peirce reflected that Kant's entire system of thought stood on his logic, in particular on his analysis of propositions. He then mused:
If we assume then that the logical distinctions of propositions are necessarily involved in reasoning and take their origin in the nature of the human mind, then so also do these conceptions, cause, reality, etc., which are essentially presupposed in those distinctions.... Thus, the whole system of Kant depends upon the truth and necessity of the system of formal logic which furnishes these distinctions of propositions. If the latter system is artificial, the Kantian philosophy must fall to the ground; yet even then it would seem that there must be in place of that a true system which would be based in a similar way upon the correct analysis of formal logic.
But, he concluded, Kant's system is artificial: "the traditional distinctions of propositions rest nearly all of them upon mere accidents of language." In Kant's wake, Peirce was ready to put forward "the correct analysis of formal logic" upon which "a true system" of thought might be founded: "there are three conceptions which enter necessarily into formal logic at every turn and under a thousand shapes,—namely, the ideas of First, Second, and Third; or, more accurately expressed, An, Other, and Medium." Here we have a preview of what was to come, a new architectonic system of thought based on Peirce’s categories to replace Kant's. In his finished review, but more intensely in items 34-37, Peirce worked out the revisions to his theories of categories and signs in his quest for "the correct analysis of formal logic." These papers constitute the spadework for his new system of thought—his architectonic evolutionary philosophy—and are the precursors of his book "One, Two, Three."
Three reviews from the latter part of 1885, which are included in the present volume, may have contributed to—or resulted from—the resumption of Peirce’s interest in speculative philosophy. In November Peirce reviewed Raymond Perrin's Religion of Philosophy for the Nation (item 39). Even though he was thoroughly unimpressed with the book, it is interesting that Perrin's purpose, revealed in the paragraph-long full title, was to reduce "the categories of thought, or the most general terms of existence, to a single principle, thereby establishing a true conception of God." Around the same time Peirce reviewed Thomas K. Abbott's translation of Kant's Introduction to Logic (item 40) and John Fiske's The Idea of God (item 41). The review of Kant's Logic is unfinished, but there is enough to see that Peirce’s reassessment of Kant occasioned by his response to Royce is uppermost in his mind. In his one-paragraph review of Fiske, unpublished and probably unfinished, he refocuses directly on the old "Design and Chance" conceptions of evolution and chance, but perhaps more importantly on what elements are necessary for explaining the "whole development of the world." Peirce mentions in particular Fiske's claim that the events of the universe are the result neither of chance nor of blind necessity, and he counters that "minds ... formed under the influence of physical science" hold that events are brought about by force and chance and that the place of freedom, if granted at all, is very limited as compared with that of necessity. Of course Peirce was one of the physical scientists who granted a small, though profoundly important, role for freedom. A fourth review in late 1885—of Clifford's Common Sense of the Exact Sciences published in the Nation on 3 September (item 38)—does not address architectonic or cosmological questions of the sort touched on above, but it does contain an early indication of Peirce’s relativism—absolute position in space and absolute velocity have no meaning. Also in the review is an interesting reference to the ideas of Peirce’s old school friend Francis Ellingwood Abbot, who was within a few days of finishing his Scientific Theism.
In the closing months of 1885, Peirce formulated the general outlines of the project that would grow into his 1887-88 "Guess at the Riddle." Although there is no full articulation of his guess to be found in the writings of 1885, it is clear from the final incomplete paragraph of item 35 that he had already made it. In his 25 October letter to Jem (quoted below), he spoke of the "momentous thing" he had to say and on its importance for molecular science and psychology. Three days later he wrote to William James (in the same letter in which he mentioned his review of Royce): "I have something very vast now.... It is ... an attempt to explain the laws of nature, to show their general characteristics and to trace them to their origin & predict new laws by the laws of the laws of nature."
Peirce spent the first month of 1886 swinging pendulums in Ithaca, but was back in New York by 1 February. On the 3rd his brother Jem held a reception for him in Cambridge. Abbot was there and wrote of the proceedings in his diary:
Attended a meeting of "philosophers," including John Fiske, James, Royce, and Perry, at Prof. J. M. Peirce’s, 4 Kirkland Place, to welcome Prof. Chas. S. Peirce, of Johns Hopkins, (my classmate), and hear from him a new "logical theory of Evolution." Peirce begins with absolute or pure potentiality, with absolute chance or negation of all law, even logical, to evolve at last Absolute Being and Absolute Law—in fact, to evolve Infinity out of Zero, God out of Nothing. Brilliant, ingenious, and—impossible. Had a wine supper, during which Charley continued to spin his glistening cobweb.
Peirce had written to Abbot from Ithaca (items 44 and 45) about his new book, Scientific Theism, and had probably already written the review that appeared in the 11 February issue of the Nation (item 46). Abbot, more the iconoclast than Peirce, had spun his own cobweb which, if not glistening, was at least alluring. Abbot's would be the second book of the period to exert a considerable influence on the course of Peirce’s thought.
Having just returned from directing pendulum operations at three major universities and, as a matter of prudence, still planning for a life of science, Peirce might have held forth on a topic related to experimental science. But Abbot's diary reveals what purpose had taken hold of Peirce’s mind. Three months earlier, on 25 October, Peirce had written to Jem:
All this [the difficulties in the Survey] has awakened me to the duty of making some effort to do that thing for which I am in the world, namely, to set forth the true nature of logic, and of scientific methods of thought and discovery. I have a great and momentous thing to say on this subject. Without it, molecular science must remain at a stand-still. It must continue what it is, idle guess-work. The true theory of the constitution of matter, which can only be based on sound scientific logic, must have the most important consequences in every direction. On psychology too, which is to be the great science of the coming hundred years, logic must exert weighty influence. About logic I have something to say which other men have not thought of, and probably may not soon think of. Perhaps I cannot get an opportunity to develope this. To do it I must sit down quietly to it & to teaching, and not live in boxes.... But it is certain that so long as I stay in the Survey my destiny will not be fulfilled.
Peirce was "straining at the bit" to get back to work on his neo-Kantian architectonic, but Survey work would keep him from it for a few months longer.
After his return from Ithaca Peirce took charge of pendulum operations at the Stevens Institute in Hoboken, where the British Kater pendulums had to be measured before their return to Herschel, and again at the Smithsonian to remeasure the pendulums he had used for the operations of the past year. But as Peirce had anticipated, the Survey was changing with Thorn in control, and it soon became apparent that leadership in geodetic science was being transferred to Schott.47 Thorn did make an effort to bring Peirce around to his own way of doing things, perhaps out of a genuine appreciation of his powers, but more likely because Peirce represented a great investment on the part of the Survey; however, he never grasped the full seriousness of Peirce’s ordeal nor its disruptive effect on his capacities. Peirce, of course, wanted to proceed with his plan for gravity determinations as set out in his letters to Hilgard of 1 October 1884 (item 23) and 30 June 1885 (and reiterated in a letter of 27 October 1885 to Thorn), but he was swamped with volumes of unreduced data from years of work that had to be turned into publishable reports—which was all Thorn seemed to want. He did manage to get three short papers into print in 1886 (items 51-53) which took some account of the 1885 work at Key West, but there was still an abundance of data on gravity and on flexure to be worked up for publication and, more importantly, a major unfinished paper on the spectrum meter which represented a great outlay of time and money. There was also the report on the 1882-83 gravity work in the Arctic, carried out for Peirce by the ill-fated Greely party. Lieutenant Greely returned from Lady Franklin Bay late in 1884 to a hero's welcome, and he made it known that the work he had carried out for Peirce was for him a matter of much satisfaction. Two years had passed since he had handed over the Arctic gravity records to Peirce, and he was anxious for results. 48 There was also a lot of unreduced data from various less extensive operations, some gravitational and others metrological, and to make matters worse, Peirce now had a mass of data from the just completed gravity operations in Washington, Ann Arbor, Madison, and Ithaca. 49
In the Survey scandal of the previous year, one of the main criticisms of Peirce had been that his work was of "meager value." It is true, of course, that however great its potential, his results were not of much use until the raw data were reduced and reports were written for publication. Thorn saw the risks and in August officially relieved Peirce of his field duties so that he might devote all his time to preparing his reports.50 He wrote to Peirce on 26 October: "It seems to us here that the feeling in Congress indicates that the whole future of the pendulum work of the Survey will depend upon your success in giving us some systematic work and adequate returns for the thousands of dollars already spent in pendulum research." Thus came the end of Peirce’s long period of leadership in geodetic science for the Survey.
The year 1886 was a watershed in Peirce’s intellectual life. It was the year when his guess at the riddle of the universe became fully articulated and then grew into the hypothesis that would guide the course of his thought for years to come. By the summer, when he began writing the book that was to set out his new system of thought (items 47-50), the guess was featured in his opening chapter:
We must ... suppose an element of absolute chance, sporting, spontaneity, originality, freedom, in nature. We must further suppose that this element in the ages of the past was indefinitely more prominent than now, and that the present almost exact conformity of nature to law is something that has been gradually brought about.... If the universe is thus progressing from a state of all but pure chance to a state of all but complete determination by law, we must suppose that there is an original, elemental, tendency of things to acquire determinate properties, to take habits. This is the Third or mediating element between chance, which brings forth First and original events, and law which produces sequences or Seconds.... [T]his tendency must itself have been gradually evolved; and it would evidently tend to strengthen itself.... Here then is a rational physical hypothesis, which is calculated to account, or all but account for everything in the universe except pure originality itself. (p. 293)
On 20 August Peirce wrote to Holden at the University of Wisconsin that his "evolutionist speculation" had grown into "a great working hypothesis of science, destined to play a great part in the future." He said that the skeleton of his ideas had "filled itself out on the philosophical side, so that my book will be a real manual of philosophy, leaving no question untouched."
It is remarkable how many lines of thought came together at this point—how many influences led Peirce to his guess. The story is too complex to be given here in full—the best account so far is by Fisch51 —but a sketch of some of the main factors will further illustrate the significance of the writings of the present volume.
With his 17 January 1884 lecture on design and chance Peirce had taken a stand on the question of determinism, declaring that absolute chance was a real agency in the evolution of the universe and even in the evolution of law itself. This thesis became a fundamental doctrine of his evolutionary cosmology and was a major factor in preparing him for his guess. It is important to remember, however, that the path to "Design and Chance" was itself very complex and that the roots of Peirce’s tychist logic extend deep into his early thought.52
Although the general thesis of an evolving universe, a universe subject to the originating influence of absolute chance, was crucial to his guess, it was not in itself sufficient. It might be more accurate to say that the key was his theory of categories, which had virtually lain dormant since first expounded in 1867 (W2: item 4). Only after he had revived his theory of categories, stimulated by his study of Royce, was Peirce ready to make his guess. But what was also revived by the study of Royce was Peirce’s Kant-inspired attraction for architectonic philosophy, for system building, and the belief that in his categories he could improve on Kant. By the end of 1885 Peirce knew that by combining his evolutionary speculations with his revived and revised categories he was on to something vast.
It is not clear exactly when he started thinking of his project as the elaboration of a guess or when he first conceived of his guess as solving the riddle of the universe in the fullest sense—so that everything would be included within the scope of his solution. A number of factors have already been mentioned that probably led Peirce to think along those lines, including the books he reviewed in 1885. Another important factor was his work for the Century Dictionary, which led him to reconsider Greek philosophy. Fisch emphasizes that nearly all the Greek philosophers were evolutionary cosmologists and he flatly states that "it was by way of the Greeks, and especially by way of Empedocles, Aristotle, and Epicurus, ... that Peirce arrived at his own evolutionary cosmology." 53 In his earliest sketch of the book that was to present his new system of thought—in thirteen chapters, beginning with a chapter on fundamental conceptions and ending with one on theism—Peirce related his purpose to that of pre-Socratic philosophy: "I am going ... to propound a hypothesis about the constitution of the universe," he began, and then pointed out that the "very first philosophical conception that appeared in early Greece was that of primal matter" (pp. 294, 295). He then defended the pre-Socratic approach to the problem of accounting for the world, which was to "first determine where their account was to begin." That called for a guess! "Now every intellectual undertaking must in its inception strike out with an original ejaculation of thought. A guess has always to be made" (p. 296). It may have been these reflections that led Peirce to cast his cosmological speculations as a guess at the riddle of the universe. Thus his great project had both a distinct Kantian character—its rigorous architectonic structure with its foundation in the categories—and an equally distinct Greek character—its evolutionary and cosmological approach self-consciouly grounded on a guess.
In considering how Peirce reached the mature conception of his cosmological project, a factor not to be left out is the influence of Abbot. When Peirce had written to Abbot in December 1885 and again in early 1886 about Scientific Theism, he had said little to indicate that he was impressed with the scope of the book, which is in some respects suggestive of Peirce’s own cosmological project. It was a sort of manifesto for a "scientific theism" and introduced the Scientific Method as the new deity: "the head has been too long sacrificed to the heart in religion."54
Science maintains that the universe it knows is actual existence, perish who or what may,—affirms the uttermost reality of its own conquests,—claims to have solved by victorious wit not a few of the Sphinx-riddles propounded to mankind by the Weltgeist,—and testifies that it finds the universe intelligible wherever it can bring to bear its unfailing method of research and discovery. It indignantly spurns the sophistry which would explain away its hard-won cosmical truths as the phenomenist's merely subjective "representations"—real while he wakes, potential only while he sleeps. 55
Abbot asserted that "the great principle of the Infinite Intelligibility of the Universe is the corner-stone of Scientific Theism" and that the key to philosophy and to the explanation of the universe lies in the conception of organic teleological evolution, not in the mechanistic ideas of Spencer and Haeckel.
In his letters and review Peirce appears to have been mainly interested in Abbot's theory of reality, especially as it concerned relations. Initially he opposed Abbot: "I am not only phenomenalist, but also idealist" (p. 280)—two positions Abbot abhorred. But before long he had been converted to Abbot's view, and in his definition of "realism" for the Century Dictionary Peirce included a lengthy quotation from Scientific Theism as the primary illustration. In his first letter Peirce had indicated that he agreed with Abbot's "universal endocosmic teleology," although he showed little interest in his cosmology. But it is interesting that Abbot mentions "Sphinx-riddles" very near the time when Peirce began to conceive of his projected book as his "Guess at the Riddle" and not long before he decided that it should appear with a vignette of the Sphinx printed below the title. By 1887, or at the latest 1888, Peirce would succinctly express his guess by speculating that "three elements are active in the world: first, chance; second, law; and third, habit-taking," and then add that "Such is our guess of the secret of the sphynx" (EP 1: 277; CP 1.409-10).
But it was not only Abbot who reminded Peirce of cosmological riddles and the Sphinx. During his Johns Hopkins years he suffered two losses—one great and the other at least sobering—which somehow may have primed him for his cosmological turn and which may also shed light on his understanding of the riddle that he supposed he had solved.
Peirce’s father, Benjamin, the single greatest influence in his life, had died on 6 October 1880. Just eight months earlier, at the Peabody Institute of Johns Hopkins, he had delivered a series of six lectures on "Ideality in the Physical Sciences,"56 where he spoke of some ancient tablets, recently discovered in Nineveh, on which was recorded an account of Babylonian cosmogony.
In the first tablet are placed, side by side, the two primitive sources of creation,—Chaos and Ideality. They stand silent and immovable,—imperturbable meditation and inactive mass,—like the sphinx by the pyramid. There they might have remained eternally unproductive. But the tablet's next record is the birth of Motion.... the divine energy of creation.57
Later in the lectures Benjamin remarked that "Nature's riddles are man's intellectual nourishment.... To shrink from them is cowardice and want of faith." Peirce had been deeply shaken by the loss of his father and had almost immediately become the vehicle for the continuation of Benjamin's mathematical thought. He may well have imagined that to some extent his father's mind could live in him—and perhaps it was true that Benjamin's more metaphysical, more speculative thought found a place in his mind to rest and await a revival. In the coming years, as Peirce delved deeply into the primeval origins of the universe, he must have known that, were it possible, his father would have smiled on him.
There was another seer in Peirce’s life, the old family friend Ralph Waldo Emerson. After Emerson's death in April 1882, Peirce often raised his ghost when expressing profound thoughts, especially the elusive connection between thinking and what is thought, between seeing and what is seen. "Of thine eye I am eyebeam," says Emerson's Sphinx. In Nature, which Peirce must have known from his youth, Emerson stated the riddle more precisely—and it might have stayed in the back of Peirce’s mind as a motivation for later cosmological speculations:
The laws of moral nature answer to those of matter as face to face in a glass. "The visible world and the relation of its parts, is the dial plate of the invisible." The axioms of physics translate the laws of ethics.... This relation between the mind and matter is not fancied by some poet, but stands in the will of God, and so is free to be known by all men. It appears to men, or it does not appear. When in fortunate hours we ponder this miracle, the wise man doubts if at all other times he is not blind and deaf ... for the universe becomes transparent, and the light of higher laws than its own shines through it. It is the standing problem which has exercised the wonder and the study of every fine genius since the world began; from the era of the Egyptians and the Brahmins to that of Pythagoras, of Plato, of Bacon, of Leibniz, of Swedenborg. There sits the Sphinx at the roadside, and from age to age, as each prophet comes by, he tries his fortune at reading her riddle.58
That is the riddle. For Peirce, at the end of 1886, the universe was becoming transparent and the light of higher laws was shining through—the laws of the laws of nature. An exciting path of thought lay open to him, and he had a clear conception of where it would lead. But the book that would found a new era in philosophy was barely started. It remained for Peirce to work up the details and consequences of his grand hypothesis into a systematic philosophy that would leave no question untouched.
It would be a mistake to suppose that, while Peirce delved into cosmology and system building, he discontinued his work in logic and the foundations of mathematics. He had a remarkable capacity for carrying out concurrent investigations, and his interest in those areas continued almost unabated for the rest of his life. His short paper on the properties of number (item 45), which he typed at Ithaca on 5 January 1886, seems rather more anomalous than most other work of the period in that it does not fit easily into the context of his other studies, and it is not mentioned anywhere in his correspondence. He did participate in the university's intellectual life while he was at Cornell, and he gave at least two lectures to engineers and mathematicians. An announcement in the 3 December 1885 Cornell Daily Sun, which introduced Peirce as "the son of one of the most eminent mathematicians of [the] century," encouraged anyone interested in the mathematical intricacies of pendulum operations to attend his lecture the following afternoon: "Professor Peirce’s ready command of language, thorough acquaintance with the subject and pleasing delivery will make the occasion profitable and enjoyable." It is not unlikely that a mathematician at Cornell stimulated Peirce’s interest in number theory and that item 45 was prepared for discussion or presentation. On the other hand, after his 1880-81 work on the axioms of arithmetic, Peirce always remained interested in further developing his theory of number and related conceptions of mathematical continua, and item 45 might have been part of this ongoing study.
After Newcomb had declined to publish the continuation of item 30, Peirce did not pursue other routes to publication—and seven years passed before he would again publish on symbolic logic. But his 1886 work in logic (items 54-56) shows that he continued to write with publication in mind. These items, all incomplete, appear to be continuations of his earlier work on a general logic book (see W4: items 30, 31, and 61) that would eventually turn into "How to Reason" (more commonly known as the "Grand Logic"). Items 55 and 56 may be more directly related to the continuation of item 30, although the set of papers that Peirce had planned for the American Journal of Mathematics was probably only a reconception of the plan for his book. On the other hand, by mid-1886 Peirce was beginning to wonder how he might supplement his income, and his 1886 work may have been part of a plan he was concocting to make logic pay.
Together, these items consolidate many important logical ideas from the years immediately past, and they anticipate some key ideas that Peirce would soon develop. This is especially true of item 54 which, although to some extent elementary, contains valuable discussions of modality and possible worlds, the importance of observation and the limitations of syllogistic reasoning for mathematics, the importance of temporality for logic, and some interesting spatial conceptions suggestive of his later Existential Graphs. Peirce points out explicitly (p. 331) that part of the business of logic is to teach useful ways of constructing diagrams, and he claims that "the ordinary business of life is best conducted without too much self-criticism" (p. 327) and that ordinary day-to-day reasonings are "better performed unconsciously than they would be if we were to try to interfere with them by a captious and hypochondriac logic" (p. 328). In some respects item 54 seems to be an expansion and development of the 1880 paper on the algebra of logic, while he might have intended to further develop the 1885 paper in a second book on quantitative logic. Item 56 expands somewhat on Peirce’s revised theory of signs as set out in the 1885 paper.
Another endeavor that extended throughout the period of this volume was Peirce’s lexicographical work for the Century Dictionary. He had been recruited in 1882 by Benjamin Eli Smith, a Johns Hopkins graduate assistant who soon became managing editor for the Century, and by 1883 Peirce had begun to write definitions. He was responsible for several subject areas and contributed over five thousand definitions (see W4: lvi). Edited by the great American linguist William Dwight Whitney, the Century Dictionary still stands as America's greatest single contribution to lexicography. Peirce worked diligently on the dictionary project until he left Johns Hopkins, but it is difficult to determine exactly how much he produced during the following two years. There seems to have been a hiatus in his dictionary work after his departure from Baltimore, although by 1886 he was again hard at work on his definitions.
The method employed in the preparation of the Century Dictionary was to distribute to its contributors relevant pages from the Imperial Dictionary, for which the Century Company held rights, to serve as a basis for the new work, and then to supply them with selections of quotations using new or difficult words. Item 57 illustrates how (at a fairly early stage) Peirce carried out his work for some words in "e"; he would continue in this vein for the rest of the alphabet, until the first edition appeared in 1889-91. But even then Peirce’s dictionary work was not finished, for he set to work at once rewriting definitions for a supplement that appeared in 1909. (A fuller account of Peirce’s lexicographical work will be given in W7, which will include a substantial selection of his published definitions.)
It is perhaps a fitting sign of Peirce’s mind that at the close of 1886 he paused from his logical and cosmological speculations, and from his lexicographical work, to point out to his former student, Allan Marquand, the key to moving from one age of computing to the next. With his simple circuit diagrams (item 58) Peirce provided the clue that might have opened the way to modern electrical computing. But even though Marquand followed Peirce’s advice and had elaborate wiring diagrams drawn up,59 and although reference to these diagrams was made in the article on logical machines in Baldwin's Dictionary, it was to no avail. Peirce probably should have pursued his idea, but he was not really very interested in computing, for he did not conceive of computers capable of effective inductive reasoning—especially weak inductive reasoning—which he believed to be the foundation of human intelligence.
Looking back, we see that Peirce’s stint at Johns Hopkins had been a time of great originality and remarkable accomplishments (recounted in the introduction to W4), accomplishments due in part to stimulation from brilliant colleagues and students. Yet in the short period of the present volume we see an even greater concentration of brilliance. There may not be a richer three-year stretch in Peirce’s life, nor one that gave rise to so many critical turning points. It is true that many of his most remarkable advances were continuations of work begun earlier; for example, his 1885 contributions to logic were direct outgrowths of a creative surge that had begun as early as 1879 and should be regarded as fruits of his Johns Hopkins experience. But we cannot say the same for his philosophy, where his creative surge began with the "Design and Chance" lecture of January 1884. Although there were many influences that led to that lecture, the ideas expressed there stand out as a starting point for a new line of thought.
It is hard to tell what really set Peirce going in a new direction—what actually moved him. Perhaps the shock of his dismissal from Johns Hopkins (and thus from university life) threw him into the state of disequilibrium—a state soon intensified by his troubles at the Survey—that triggered his creative energy. The finality of his dismissal and the shocking discontinuity it forced on the course of his life must have brought a kind of freedom, a time when he could look forward without looking back. At such times, fresh ideas, either new or drawn from some reservoir of the past, are likely to have unusual impact—especially when they are in conflict with a present course of thought. So in early 1884, at the most pronounced moment of disruption and uncertainty in Peirce’s life, he surrendered to his long-held attraction for the idea of the efficacy of chance. He opened his lecture on design and chance by remarking on a new element in intellectual history: the tendency to question the exact truth of axioms. By the summer of 1886 he would begin his book on the categories with the abrupt assertion: "This is the day for doubting axioms" (p. 292). In Peirce’s own words we have a good summation of where he stood at the time.
To assess how the work in this volume contributes to the overall development of Peirce’s thought—a task far too complex to be fully addressed here—it will be helpful to follow the guidance of Fisch and Murphey. The measure Fisch uses to gauge Peirce’s general intellectual development is how far he had progressed from his early nominalism (some say his early weak realism) toward his ever more encompassing realism.60 In Fisch's broadest characterization Peirce can be classified as a one-, two-, or three-category realist, depending on whether he acknowledged the reality of Thirdness, of Thirdness and Secondness, or of all three categories. Peirce did not accept the reality of actuality, or Secondness, until about 1890, and it was seven years later, in 1897, when he finally accepted the reality of possibility, or Firstness—and only then became a three-category realist. Thus, during the period of the present volume, Peirce was still a one-category realist, accepting only the reality of Thirdness. However, his intellectual progress did not occur in two or three great leaps but in a series of many steps. Some of the most significant developments leading to his acceptance of the reality of Secondness are directly related to the work of this period. According to Fisch, these include
his work on the logic of relations and on truth-tables, indices, and quantification; the resulting reformulation of his categories; his work and that of Cantor and Dedekind on transfinite numbers; the appearance in 1885 of provocative books by Royce and Abbot; and ... a fresh review of the history of philosophy for purposes of defining philosophical terms for the Century Dictionary.61
Murphey divides Peirce’s intellectual development into four periods or systems, each characterized by a distinctive approach to the categories. Peirce’s growth from his earliest to his latest system of thought was the result of successive discoveries in logic, each requiring revisions to the categories because of Peirce’s architectonic approach to philosophy. Murphey and Fisch agree that it is how the categories stand in relation to Peirce’s theory of reality that best measures his development.
When the period covered by the present volume began, Peirce was just entering the final and longest phase of his intellectual life, according to Murphey's account. The logical discoveries that led Peirce to this final phase were his discoveries of quantification and set theory. In particular it was Peirce’s discovery of the index, following Mitchell, that led him to understand the importance of individuality and of reference to the individual.62 Fisch also emphasizes the importance of this discovery and points out that it forced Peirce to revise both his theory of signs and his theory of categories. It was at this time that Peirce began to stress that "the actual world cannot be distinguished from a world of imagination by any description. Hence the need of pronouns and indices" (p. 164). Toward the end of 1885, in his review of T. K. Abbott's translation of Kant's Logic (item 40), Peirce remarked that Kant's statement that no general description of existence is possible "is perhaps the most valuable proposition that the Critic contains."
According to Murphey, Peirce’s new understanding of the fundamental importance of reference to the individual led him to abandon his definition of reality as "that which is thought in the final opinion to which inquiry will lead," which equates the real with the end of a series of cognitions.63 That theory of reality was a constitutive doctrine. Murphey says that sometime between 1880 and 1890 Peirce abandoned the constitutive principle for a weaker regulative principle, which held only that "in order to make certain that agreement will be pursued it is necessary to hope that ultimate agreement will come." Peirce’s 1885 study of Royce may have played the essential role in leading him to this revision. There Peirce claimed that a skeptic (like himself) can fruitfully embrace God's omniscience "as a regulative but not a speculative conception" (p. 229). Christopher Hookway also points to that review as giving an early account of Peirce’s "moderate fallibilism." 64
Other important doctrines and themes in Peirce’s later thought seem also to be prefigured, if not directly grounded, in the writings of this volume. For example, in the Royce review just cited, Peirce briefly discusses his theory of the existence of God, which he says he hoped soon to get into print: "I think that the existence of God, as well as we can conceive of it, consists in this, that a tendency toward ends is so necessary a constituent of the universe that the mere action of chance upon innumerable atoms has an inevitable teleological result." We can see here the interplay of Peirce’s theology with his methodology and cosmology and that his conception of chance had begun to spread throughout his thought. Earlier in this period, in April 1884, he had asked to teach a fall course at Johns Hopkins on the logic of religion, and in May he had delivered a paper on that subject to the Metaphysical Club, where he discussed proofs of the existence of God (see W4: p. lxvi). It was noted above that the final chapter of "One, Two, Three," Peirce’s projected treatise on evolutionary cosmology, was entitled "Theism."
There are other "turning points," not mentioned above, that belong to this time. For example, Peirce’s reading of Kempe's 1886 "Memoir on the Theory of Mathematical Form" (cf. MS 583) was an important stimulus in turning his thoughts to logical diagrams and the development of his Existential Graphs. 65 And there are indications that his study of Abbot's Scientific Theism may have led him to investigate how relations are represented in thought and to reflect deeply on the importance of diagrams for understanding thinking as a process (see pp. 287-88). Also in the Abbot review there is an early statement of Peirce’s vortex solution to the mind-body problem.
But while these years represent a new beginning in the development of Peirce’s philosophy, they effectively mark the end of his life of science. It is true that he spent the next few years working up scientific results for publication and he sometimes attempted to revive the goodwill he once had in the Survey (until his forced resignation on 31 December 1891), but he was never again given the chance to work in the field as a professional geodesist. In 1899 he tried to reenter the world of professional science as head of the newly formed Bureau of Standards, but he was foiled again by Newcomb, his old nemesis.66 Occasionally Peirce would resume old investigations such as his study of color—he began some color experiments in June of 1886 which continued until June of 1887—but most later work in experimental science was sporadic and connected with some scheme or other in his (never successful) quest for prosperity. It is ironic that Peirce’s geodetic work continued to contribute and even to bring great credit to the Survey, though without acknowledgment or benefit to him.67
For his life in general, these years were a time of dislocation and uncertainty—a mid-life crisis of massive proportions and in the most literal sense. This is reflected early in the period in a 1 May 1884 letter from his mother: "I am longing to hear of your cologne water, your lectures, your Actuaryship & whatever other schemes you may have thought of & trust they will not all die out 'like the baseless fabric of a vision.'" (Peirce had concocted a cologne water that he hoped to market.) Was his mother paraphrasing her late husband, Charles's father: "how can we be sure that our intellectual picture of the external world is not a human creation, and the fabric of a vision?"68 She wrote again the following month, on 6 June:
I have received to-day the little bottle of Cologne you promised me for my pocket! Now I must enlarge my pockets or your intention cannot be carried out to the letter! ... soon I suppose you will be leaving Baltimore for the summer. Oh! my dear Charley—how much I feel for your discouragements, & troubles—& how I wish I could in any way help you! At such times how much we all miss your dear Father—always so ready with advice of the best kind, & any possible help for you all! I hope you will not resign from the CS. until you are sure of something better.
As the years progressed, Peirce’s attention shifted, often abruptly and erratically, between science and philosophy. When 1886 came to an end, his mind must have been a swirl of ideas about logic and categories and evolutionary cosmology—and about the various scientific reports he was working hard to finish. But prominent in his consciousness was the realization that somehow he had to make a living. For the life he wanted—the life he had promised Juliette—he needed more money than he could make at the Survey, and even that source of income was tenuous. Perhaps Juliette could go on stage—it was said that she had great talent. In 1886 she began to study acting with Steele MacKaye, New York playwright and theater manager, and Peirce toyed with the idea that she might become a great success: "then a difficult question will arise for me between my duty to Humanity in the abstract, and my duty to this Lady in the concrete."69 But Peirce knew that this was not the solution to his financial problems. Was there not a way to make a living from what he knew best: logic? He finished the period making plans. On 4 January 1887 he wrote to his cousin, Henry Cabot Lodge, asking for a short-term loan to fund a new venture:
I have quite a reputation for my knowledge of the logic and methods of science. I have worked out a long series of practical exercises to teach the whole art of reasoning from beginning to end. There are throughout the country thousands of young men and women to whom these lessons would be of more real service than almost anything they could study. The question is, first, how many of them I could teach. Now I have planned a system which I won't trouble you with, with passages written out answering every conceivable difficulty in the whole course, type-writers, and assistants (upon whom I can lay my hands when I need them) by which I can write say 500 letters a day, or take charge of 1500 students. I propose to charge $30 in advance for 30 lessons, the entire course being about 200.... I want to begin by sending out a hundred thousand [circulars] in order to ascertain what number of circulars has to be sent to gain one scholar in the long run. I guess about a thousand.... This scheme, or some modification of it which I will find, must pay.
Peirce did not get the loan, but his circular was already written and would soon appear in The Century Magazine and other popular publications. If he could not live his life teaching logic at a university, he would make his living teaching logic in some other way. 70 So he thought.
Nathan Houser
Notes
1 In writing this introduction, I have depended a great deal on the results of Max H. Fisch's many years of research, contained in his files at the Peirce Edition Project. The best accounts of Peirce’s intellectual development are in Fisch, Peirce, Semiotic, and Pragmatism, eds. Kenneth L. Ketner and Christian J. W. Kloesel (Bloomington: Indiana University Press, 1986) and Murray G. Murphey, The Development of Peirce’s Philosophy (Cambridge: Harvard University Press, 1961). For a general account of Peirce’s life, see Joseph Brent, Charles Sanders Peirce: A Life (Bloomington: Indiana University Press, 1993).
To reduce the number of footnotes, I do not give references for items that can be easily located by keeping the following in mind: all manuscript references (according to either the Peirce Edition Project or Harvard arrangement) are to the Peirce Papers at Harvard University which also contain the correspondence between Peirce and the members of his family; correspondence with employees of the Coast Survey is in Record Group 23 in the National Archives. NEM refers to The New Elements of Mathematics, ed. Carolyn Eisele (The Hague: Mouton, 1976), and EP to The Essential Peirce, eds. Nathan Houser and Christian Kloesel (Bloomington: Indiana University Press, 1992).
2See Fisch, p. 227.
3Discussed in W2 Introduction, pp. xxxi-xxxiv.
4See Murphey, p. 3.
5See Oscar Howard Mitchell, "On a New Algebra of Logic," in Studies in Logic, ed. C. S. Peirce (Boston: Little, Brown, & Co., 1883), pp. 72-106.
6Quoted in Fisch, p. 233.
7See Murphey, ch. 15.
8For more on Peirce’s life during the early months of 1884, see W4: xxxv-xxxvi and lxii-lxx.
9For a fuller account of the impact of Peirce’s dismissal on his life, see Brent, ch. 3.
10See also the note for 139-43.
11See, for example, CP 7.256-66, where the study is described in some detail.
12The New Calendar of Great Men: Biographies of the 558 Worthies of all ages and countries in the Positivist Calendar of August Comte, ed. Frederick Harrison (London: Macmillan, 1892).
13Peirce to Lowell, 6 December 1891. Quoted in Carolyn Eisele, Studies in the Scientific and Mathematical Philosophy of Charles S. Peirce, ed. R. M. Martin (The Hague: Mouton, 1979), pp. 141-42.
14See Thomas A. Sebeok, Semiotics in the United States (Bloomington: Indiana University Press, 1991), pp. 114-15.
15"Joseph Jastrow," in A History of Psychology in Autobiography, ed. Carl Murchison (Worcester, MA: Clark University Press, 1930), vol. 1, pp. 135-62.
16See Thomas C. Cadwallader, "Charles S. Peirce (1839-1914): The First American Experimental Psychologist," Journal of the History of the Behavioral Sciences 10 (1974): 291-98.
17Quoted in Eisele (1979), p. 87.
18Stephen M. Stigler, "Mathematical Statistics in the Early States," Annals of Statistics 6 (1978): 248.
19See Ian Hacking, "Telepathy and Randomization," Isis 79 (1988): 427-51.
20R. A. Fisher, The Design of Experiments (Edinburgh: Oliver & Boyd, 1935).
21Science (17 October 1894): 370. References to the Society had appeared even earlier in the popular press.
22See Arthur N. Prior, "The Algebra of the Copula," in Studies in the Philosophy of Charles Sanders Peirce, eds. Edward C. Moore and Richard S. Robin (Amherst: University of Massachusetts Press, 1961), pp. 79-84.
23See W4: xlvi-xlvii and note 184.3 for further discussion of the 1880 "Algebra of Logic."
24See Irving Anellis, "Forty Years of 'Unnatural' Natural Deduction and Quantification," Modern Logic 2 (1991): 113-52, especially 115. For another discussion of Peirce’s anticipation of Gentzen, see Don D. Roberts, "The Existential Graphs and Natural Deduction," in Moore and Robin, pp. 109-21.
25Stigler (1978), 249.
26See Thomas G. Manning, Government in Science (Lexington: University of Kentucky Press, 1967), pp. 122-23.
27See Fisch, p. 409.
28Quoted in Eisele (1979), p. 82.
29See Thomas G. Manning, "Peirce, the Coast Survey, and the Politics of Cleveland Democracy," Transactions of the Charles S. Peirce Society 11 (1975): 187-94. See also Brent, ch. 3.
30See Manning (1975), 188.
31The source of the "meager value" remark appears to be a disposition of B. A. Colonna on the condition of the Survey (see L91a: 127).
32Peirce to Powell, 2 May 1886; quoted in Manning (1967), pp. 138-39.
33For a fuller account of the Gautier pendulum episode, see W4: xxxiv and Brent, pp. 140-41, 164, and 177.
34See Victor F. Lenzen, "An Unpublished Scientific Monograph by C. S. Peirce," Transactions of the Charles S. Peirce Society 5 (1969): 5-24.
35See also item 62 in W4.
36This principle has been known since Lukasiewicz as Peirce’s Law.
37See Atwell R. Turquette, "Peirce’s Icons for Deductive Logic," in Moore and Robin, pp. 95-108, especially p. 101.
38See Richard Martin, Peirce’s Logic of Relations and Other Studies (Dordrecht, Holland: Foris Publications, 1980), p. 63.
39See J. Jay Zeman, "Peirce’s Philosophy of Logic," Transactions of the Charles S. Peirce Society 22 (1986): 1-22, especially 7.
40See Henry Hiz, "Peirce’s Influence on Logic in Poland," forthcoming in Studies in the Logic of Charles Sanders Peirce, eds. Nathan Houser, Don D. Roberts, and James Van Evra (Bloomington: Indiana University Press, 1994).
41See Irving Anellis, Review of Volumes 1-4 Writings of Charles S. Peirce, Modern Logic 3 (1992): 77-92, especially 87.
42See item 56 for a related but somewhat fuller presentation of Peirce’s revised theory of signs.
43In one recollection of this incident (cited in NEM 3: 1069), Peirce said that Newcomb rejected a proposal on the grounds that the planned work was not mathematics and that, as a result, the paper remained unwritten. If that was the case, items 31 and 32 may constitute Peirce’s most finished results. But Peirce’s earlier accounts tend to confirm that he submitted a finished paper for publication.
44NEM 3: 816-17.
45Brent, p. 174.
46Fisch, pp. 190-91.
47See Brent, p. 177.
48Peirce’s report on the Arctic gravity work will be included in W6, and a more detailed account of the Peirce-Greely interaction will be given in the introduction to that volume.
49See Brent, pp. 196-201.
50Victor F. Lenzen, "Charles S. Peirce as Mathematical Geodesist," Transactions of the Charles S. Peirce Society 8 (1972): 90-105, especially 98.
51See Fisch, ch. 12.
52See W4: lxvii-lxix; Fisch, ch. 12; and Brent 171-73. An excellent account of Peirce’s early indeterminism, especially as developed in his 1866 Lowell Lectures, was given by Paul D. Forster in Toronto on 9 October 1992: "The Logical Foundations of Peirce’s Indeterminism" will be published in the proceedings of the conference, entitled "New Topics in the Philosophy of C. S. Peirce" and held at Trinity College, University of Toronto.
53Fisch, p. 233.
54Francis Ellingwood Abbot, Scientific Theism (London: Macmillan, 1885), p. 217.
55Ibid., pp. 121-22.
56These lectures were first given at the Lowell Institute in Boston in 1879. They were edited by Jem after Benjamin's death and published in 1881.
57This and the immediately following quotation are from Benjamin Peirce’s Ideality in the Physical Sciences (Boston: Little, Brown, and Co., 1881), pp. 43-44 and 183.
58This quotation, and the idea that it may be connected with Peirce’s guess, appears in an unpublished manuscript by John Sheriff.
59See Kenneth Laine Ketner, "The Early History of Computer Design," Princeton University Library Chronicle 45 (1984): 187-224.
60See Fisch, ch. 10.
61Fisch, p. 189.
62Indices do appear in Peirce’s earlier work, especially in his "New List" (W2: item 4), but not as signs that refer directly to individuals. See Murphey, pp. 299-300.
63Murphey, p. 301.
64Christopher Hookway, Peirce (London: Routledge & Kegan Paul, 1985), p. 73.
65See Don D. Roberts, The Existential Graphs of Charles S. Peirce (The Hague: Mouton, 1973), pp. 20ff.
66See Brent, pp. 152 and 266-67.
67Ibid., p. 198.
68B. Peirce (1881), p. 23.
69Peirce to E. S. Holden, 20 August 1886.
70 Selections from Peirce’s correspondence course in logic will be included in the next volume of the present edition.
Original readings are given in brackets after the correction.
1 July ’67 [1 Dec.] line to be moved after l. 17 in Chronology
1886 [1885]
fifth [fourth]
The diagram was printed backwards and without the capital letters identifying each line. See below an explanation with an image of the correct diagram.
The two electric circuit diagrams should be labeled respectively Fig. 1 and Fig. 2 underneath.
See De Morgan’s “On the Syllogism, No. IV,” 1864, App. pp. *355–*358. [See De Morgan’s “On the Structure of the Syllogism [No. I],” pp. 406–408.]
p. *356. [p. 353.]
(907, 909). [(906, 909).]
(532, 547). [(532).]
provided in the introduction, pp. xxxii–xxxiv. [included in the item 30 headnote.]
371 [361]
The Project provided the following explanation of the error in the first issue of its newsletter (volume 1, no. 1, March 1994, under the title “Oops… We Got it Backwards”)
Careful readers of W5: item 36 (“Measurement Scales and the Absolute”) may have noticed that the example Peirce discusses on p. 250 doesn’t seem to apply to either of the diagrams in the item. That’s because we slipped up. The fact is, Peirce’s discussion on p. 250 is about the diagram on p. 249. Our copy editor prepared a nice piece of line art for p. 249 with letters carefully pasted in, but in production the glossy diagram was reversed by the layout people at the Press and was photographed from the back, which nicely shows the lines but without the pasted-on letters.
 Fig. 1
Fig. 1
Before the proof pages came back, the Project had lost its copy editor (one of the positions eliminated when the Project lost its NEH grant) and probably as a result the mistake was overlooked. Even though the diagram as printed in W5 is left-right reversed, it will serve perfectly well for Peirce’s discussion if it is labeled as in the following way. First label the intersecting point of the vertical and horizontal lines “E”. Next, label the intersecting point of the boldface diagonal lines “X”. Then label the endpoints of the boldface lines as follows: make the upper left “A”; the lower right “B”; the upper right “C”; and the lower left “D”.
Below is the diagram as it was meant to appear.
 Fig. 2
Fig. 2
“To erect a philosophical edifice that shall outlast the vicissitudes of time, my care must be, not so much to set each brick with nicest accuracy, as to lay the foundations deep and massive.”
Volume 6 contains 47 writings—most from the unsettled period in Peirce’s life that began as he moved from New York to Milford, Pennsylvania, in April 1887, a move followed six months later by the death of his mother. It was more than a year after moving to Milford before Peirce and his second wife, Juliette, took possession of Arisbe, their final home. Peirce’s preoccupation during this time with getting established in Milford, and later with renovations to Arisbe, interfered with his intellectual pursuits. Nevertheless, his rekindled interest in speculative philosophy, following his untimely separation from Johns Hopkins University, continued to motivate him during these years. His thought was also influenced by other forces, including the opinions of friends and colleagues in Cambridge and New York, urgent pleadings from the superintendent of the U.S. Coast and Geodetic Survey that he complete his gravity reports, and the ever-present need to turn writing into cash. Peirce hoped to make a good living by teaching logic through correspondence.
Volume 6 begins with interesting remnants of that correspondence course in logic, including how Peirce applied nineteenth-century marketing methods to promote it with the help of agents, and a sample of his lessons and of his epistolary exchanges with students, for the most part puzzled to no end by the rudiments of Boolian algebra. Other notable selections include the much-heralded chapters of “A Guess at the Riddle,” Peirce’s never-finished yet substantial attempt to integrate his broad sweep of philosophical theories into a unified system of thought, testing the heuristic power of his three categories in disciplines such as logic, psychology, physiology, biology, and physics, and then generalizing those categories to the entire realm of inquiry; his methodological dispute with Edmund Gurney over Gurney’s large survey of testimonies of manifestations of the dead detailed in Phantasms of the Living; his inquisitive attack, fortunately under the pseudonym “Outsider” (given the harsh responses it elicited, especially from members of the Brooklyn Ethical Association), on Spencer’s mechanical philosophy at a time when Spencer’s theories were at the height of their popularity; and lengthy excerpts from the never published report on gravity that led to Peirce’s forced resignation from the U.S. Coast and Geodetic Survey (the editing of that report will long remain one of the most complex editorial feats in the history of the Peirce Project). According to Victor Lenzen, this gravity report shows Peirce at his scientific best and would have been a major contribution to geodesy had it been duly published.
These and other writings in this volume (on science and immortality, on spiritualism, on logical machines, on the logic of science, on geometry, on relations) reveal Peirce’s powerful mind probing into diverse issues, looking for an underlying unity but, perhaps, also looking for direction. Part of Peirce’s investigation was stimulated by his continuing research on scientific and mathematical definitions for the great Century Dictionary with which he became associated in 1883.
“The reasonings and conclusions of the mathematician do not in the least depend upon there being in the real world any such objects as those which he supposes.”
| Preface | xiii | |
| Chronology | xix | |
| Bibliographical Abbreviations in Editorial Matter | xxiii | |
| Introduction | xxv | |
| 1. | Boolian Algebra-Elementary Explanations | 1 |
|
CORRESPONDENCE COURSE ON THE ART OF REASONING |
||
| 2. | [Circular for Course on the Art of Reasoning] | 10 |
| 3. | [Follow-up Letter to Circular] | 15 |
| 4. | A Few Specimens of Exercises in the Art of Reasoning | 19 |
| 5. | Directions to Agents | 21 |
| 6. | [Letter to New Students] | 33 |
| 7. | [Orientation Letter to Marie Noble] | 35 |
| 8. | [Letter to Noble on the Nature of Reasoning] | 37 |
| 9. | [Reasoning Exercises: Number Series, Relational Graphs, and Card Games] | 41 |
| 10. | Boolian Algebra [Three Lessons] | 50 |
| 11. | [Two Letters from J. B. Loring on Algebra Lessons] | 54 |
| 12. | [Reply to Loring] | 56 |
| 13. | [Additional Exercises in Boolian Algebra] | 58 |
| 14. | [Science and Immortality] | 61 |
| 15. | Logical Machines | 65 |
|
THE PEIRCE-GURNEY DISPUTE OVER PHANTASMS OF THE LIVING |
||
| Cases Abstracted from Phantasms of the Living | ||
| 16. | Criticism on Phantasms of the Living: An Examination of an Argument of Messrs. Gurney, Myers, and Podmore | 74 |
| 17. | Remarks on Professor Peirce’s Paper (by E. Gurney) | 82 |
| 18. | Mr. Peirce’s Rejoinder | 101 |
| 19. | Remarks on Mr. Peirce’s Rejoinder (by E. Gurney) | 142 |
| 20. | Number | 155 |
| 21. | Logic of Number | 156 |
|
A GUESS AT THE RIDDLE |
||
| 22. | [Contents] | 166 |
| 23. | Chapter I. Trichotomy | 168 |
| 24. | [Chapter III.] The Triad in Metaphysics | 181 |
| 25. | Chapter IV. The Triad in Psychology | 182 |
| 26. | Chapter V. The Triad in Physiology | 188 |
| 27. | Chapter VI. The Triad in Biological Development | 199 |
| 28. | Chapter VII. The Triad in Physics | 203 |
| 29. | [Trichotomic] | 211 |
| 30. | Pendulum Observations at Fort Conger | 216 |
| 31. | Reflections on the Logic of Science | 246 |
| 32. | Note on the Analytical Representation of Space as a Section of a Higher Dimensional Space | 260 |
| 33. | Ordinal Geometry | 263 |
| 34. | [Mathematical Monads] | 268 |
| 35. | Review of Stock's Deductive Logic | 271 |
| 36. | Report on Gravity at the Smithsonian, Ann Arbor, Madison, and Cornell | 275 |
| 37. | [Reasoning] | 354 |
| 38. | On a Geometrical Notation | 357 |
| 39. | On the Numbers of Forms of Sets | 360 |
| 40. | The Formal Classification of Relations | 363 |
| 41. | Dual Relatives | 368 |
| 42. | Notes on Geometry of Plane Curves without Imaginaries | 372 |
| 43. | Review of Noel's The Science of Metrology | 377 |
| 44. | [Logic and Spiritualism] | 380 |
| 45. | Herbert Spencer's Philosophy | 395 |
| 46. | Review of Collins's Epitome of the Synthetic Philosophy | 401 |
| 47. | "Outsider" Wants More Light | 402 |
| Editorial Symbols | 413 | |
| Annotations | 417 | |
| Bibliography of Peirce’s References | 506 | |
| Chronological Catalog, January 1887-April 1890 | 512 | |
| Supplement to W5 Chronological List, 1884-1886 | 531 | |
| Essay on Editorial Theory and Method | 534 | |
| Textual Apparatus | 557 | |
|
Headnotes, Textual Notes, Emendations, Rejected Substantives, Alterations, Line-End Hyphenation |
||
| Line-End Hyphenation in the Edition Text | 672 | |
| Index | 673 | |
The period from 1887 through the spring of 1890, though not without hope and accomplishment, was a time of disillusionment and defeat for Peirce. 1 Only a few years earlier, Peirce’s father, Benjamin, the great mathematician and astronomer, had proudly proclaimed to the Boston Radical Club that his son Charles would carry on his life's work and would develop and fertilize vistas he had only glimpsed. No one doubted it. Charles's star was rising. During the first half of the 1880s, he was one of America's elite scientists and the only American logician known the world over. Peirce had just begun teaching at Johns Hopkins and had every reason to expect that he would spend his life there as Professor of Logic. But in April 1883, Peirce divorced his first wife, Melusina Fay, and married his reputed mistress, Juliette Froissy Pourtalais, a woman of unknown, or at least of unspoken, origin. 2 Nothing for Peirce would ever be the same again. Within a year he had been forced out of Johns Hopkins and by 1886 his scientific career with the Coast and Geodetic Survey was falling apart. By 1887 Peirce had come to be spurned by the society that had nurtured him—he was no longer welcome even in his family home. A sense of defeat grew in Peirce as he struggled with the realization that all the paths he had chosen were blocked and that he could neither have the life he wanted nor provide for Juliette the life her extravagant tastes demanded. In April 1887, Peirce and Juliette packed up and moved to Milford, Pennsylvania, a mountain village with a small but thriving French community, where they hoped to make a new start and where they imagined they could afford to live well. At first Peirce expected his exile to be temporary but he soon came to understand that he would be a man apart. When in the spring of 1890, mainly for the income, he helped organize a journalistic attack on Herbert Spencer, Peirce signed his contributions "Outsider." That is what he had become.
In 1884, after his dismissal from Johns Hopkins, Peirce moved to Washington D.C. to refocus his career on his scientific work for the Coast and Geodetic Survey. In July he had begun an intensive program of field operations which he expected to continue until a vast expanse of the continental United States was linked through gravity determinations and added to the international geodetic network that would serve to calculate the figure of the Earth. This was a principal concern of mathematical geodesy and Peirce had already contributed to its solution (W4: sel. 76). At some point he knew he would have to turn a growing mass of data into a publishable report on gravity, but he kept putting it off in favor of continued field work. He assumed that when the time came to prepare reports he would have whatever computing help he needed, as he always had before. Then in March 1885, Grover Cleveland was inaugurated as the twenty-second President of the United States and Peirce’s plans were dashed. Cleveland came to power intent on reforming government service and by July had targeted the Coast Survey as the agency he would make an example of. 3 Superintendent Julius Hilgard was fired and all administrators and field officers, including Peirce, were subjected to intense scrutiny. Frank Manly Thorn, a lawyer and friend of Cleveland, was installed as acting superintendent to carry out the President's reform agenda. Greatly discouraged by what was happening, Peirce left Washington in March 1886 and moved with Juliette to New York City. He supposed that New York would be a better place to start a new life in case his Survey job should be lost. He carried out pendulum field operations at the Stevens Institute station in Hoboken until August when Thorn relieved him of further field duty and ordered him to prepare for publication the backlog of results already obtained. Funding for field operations had been slashed and Peirce’s gravity work, among the most costly, could no longer be supported. If pendulum operations were to continue they would have to be scaled back to meet only the demands of practical science, not those of pure science that guided Peirce. On 20 August Peirce wrote to University of Wisconsin astronomer, Edward S. Holden: "The president seems to have decided to keep Thorn in as Superintendent as long as he can, and under the influence of these men of Red Tape all the life and energy has gone from the Survey. . . . I am utterly discouraged and disgusted, and want to get out. . . ." In October, trying to cheer him up, Peirce’s mother wrote: "Cleveland is a Dolt."
Somehow Peirce managed to hang on to his Survey job for another five years, although it seems certain that he would have given it up many times over had he not needed the income so desperately. Peirce was clearly disaffected and frequently spoke of resigning, but then always reconsidered. His relations with Survey headquarters became increasingly strained, sometimes quite bitter, and except for brief periods of respite, the remainder of his tenure was marked by a suspicion in Washington that Peirce was not doing enough work and by a concern on Peirce’s part that there was a cabal conspiring to get him dismissed. One period of promise came just after July 1889 when Thomas Corwin Mendenhall, a trained scientist, succeeded Thorn as Superintendent. But it soon became evident that Mendenhall's plans for gravity determinations left no room for pendulum operations of the sort Peirce practiced. By the close of the period covered in the present volume, Peirce’s second major gravity report, representing years of labor, was at risk of being rejected for publication, and Mendenhall's patience with Peirce was rapidly reaching its limit.
Amidst the turmoil of a life in constant transition and a career that was falling apart, Peirce managed to carry on at least a thread of philosophical inquiry, inspired in part by his late work at Johns Hopkins and his reading of the 1885 books by Royce and Abbot, and fueled by his continuing lexicographic research for the Century Dictionary . 4 In the August 1886 letter to Holden quoted above, Peirce added: "You remember that I told you something of a sort of evolutionist speculation of mine. This has grown much. . . ." When he wrote to Holden, he had already begun to write a book entitled One, Two, Three in which he would make a guess about the constitution of the universe and use his categories as the key to an all-encompassing system of philosophy (W5: sels. 47-50). After his move to Milford in 1887 this work would grow into his "A Guess at the Riddle" (sels. 22-28) and, although never finished, it would set the course for much of his subsequent thought. But as 1886 drew to a close, it was logic that was uppermost on Peirce’s mind. For a while he resumed work on a book on general logic (W5: sel. 54) which would evolve into his "How to Reason" of 1894. But as his insecurity with his career increased, his interest turned from the advancement of the science of logic to how he could use his specialty to make a living adequate to the demands of the lifestyle he and Juliette had set for themselves in Baltimore in the first months of their marriage. Peirce’s income had taken a serious hit with the loss of his lectureship at Johns Hopkins, and now that his Coast Survey salary was in danger, he had to find a substantial new source of income. He began writing elementary accounts of his logic of relatives (W5: sels. 55-56) and Boolean algebra (sel. 1), perhaps initially for a course of lectures he hoped to deliver at the University of Wisconsin, but at least in the latter case it is likely he had paying students in mind.
Peirce entered 1887 with some confidence that he had found a way to survive his anticipated separation from the Survey. Were there not hundreds, nay, thousands of citizens abroad in the land in the greatest need of improving their reasoning skills? Would not a good course in reasoning, customized for individual capabilities and taught by a master logician, increase opportunities and, in general, better the lives of students—and thereby serve well the country as a whole? Could not one expect to attract large numbers of occasional students to sign up for a course of study that virtually guaranteed a high degree of self-improvement? Peirce was convinced that he had found a niche and that with clever marketing and efficient operations he could make good money with a correspondence course on the art of reasoning. He wrote to Cyrus W. Field, financier for the first transatlantic cable, that for years he had carried in his pocketbook a clipping quoting Field on the value of right reason: "My fortune was made by working a gold-mine, and that gold-mine is the power of right reason." Peirce might not make a fortune, but surely he would make a good living.
To set this promising plan into motion, Peirce needed capital. Brochures would have to be printed, lessons duplicated, typewriters purchased, assistants hired, and field-agents engaged. Peirce wanted fifteen hundred students and imagined that once things got rolling he would send out around five hundred letters a day. He would begin by advertising in popular magazines and would send out a hundred thousand circulars. He wrote to his cousin, Henry Cabot Lodge, and asked for a loan to get his scheme off the ground. Lodge declined and apparently with no other prospects Peirce decided to start up piecemeal. In May an advertisement for his course circular (reproduced on p. 14) ran in the Century Magazine and he sent circulars (sel. 2) to seven hundred people. He wrote to his brother James Mills (Jem) that he doubted he would attract "a single pupil from so small a number," but letters of interest began to come in. Records for the course are very incomplete, so it is difficult to tell how many responded or exactly what the content of the course was, but it is clear that by the end of March Peirce had received more than fifteen inquiries and at least eight students had begun lessons. While far from what Peirce needed to make a living, and certainly not enough to let him resign from the Survey, the response was promising and indicated that a major promotional effort could succeed. Peirce imagined an army of agents dispersed throughout the country, all soliciting students to sign up for his course. He drew up directions for agents (sel. 5) which bring to mind the hucksterism of turn-of-the-century medicine peddlers or of modern telephone solicitors: "The levers upon which you have to rely are first, cupidity, second, shame, and third, fatigue." Still, there is no doubt that Peirce believed he could deliver good value for the price of his course, and from what can be reconstructed from the fragments that remain (see sels. 3 -13), that belief seems justified.
Peirce’s plan for the correspondence course was set out in his circular (sel. 2) and his follow-up letter (sel. 3). The course would be divided into three parts—traditional logic, mathematical reasoning, and scientific reasoning—and the full course would require a minimum of one hundred and eighty letters. From the exercise sets that have survived—only a small part of the series Peirce had prepared—and from surviving student letters, it is possible to get a sense of what Peirce taught and how he interacted with his students. He seems to have gone to some lengths to address his students' individual interests and capabilities, but it is likely that he was aiming too high. Certainly the reasoning exercises (sel. 9) and the three lessons in Boolean algebra with additional exercises (sels. 10 and 13) involved rather high-level logical content; there is a one-page fragment (in RL 100) that indicates that Peirce even hoped to convey some of his favorite philosophical ideas through his reasoning exercises. For example, the second exercise from the fragment gives a brief lesson in Peirce’s theory of signs:
Let us use the word "sign" to mean anything which on being perceived carries to a mind some cognition or thought which is applicable to some object. Thus, I would call a portrait a sign. I would call a pointing finger a sign. I would call a spoken sentence a sign. I now ask you to make a list of a good many different kinds of signs, and to attempt to classify them according to their different modes of standing for their objects. To do this will require a good deal of thought.
Such questions might well serve the purpose of evaluating student preparedness but they seem aimed at minds more elastic and capable than might be expected to turn out in the large numbers Peirce expected. Still, a letter he wrote at the end of March to J. M. Hantz of Northwestern University indicates continuing enthusiasm for his course and reveals no dissatisfaction with his initial students:
It is my fate to be supposed an extreme partisan of formal logic, and so I began. But the study of the logic of relations has converted me from that error. Formal logic centers its whole attention on the least important part of reasoning, a part so mechanical that it may be performed by a machine, and fancies that that is all there is in the mental process. For my part, I hold that reasoning is the observation of relations, mainly by means of diagrams and the like. It is a living process. This is the point of view from which I am conducting my instruction in the art of reasoning. I find out and correct all the pupil's bad habits in thinking; I teach him that reasoning is not done by the unaided brain, but needs the cooperation of the eyes and hands. Reasoning, as I make him see, is a kind of experimentation, in which, instead of relying on the intelligible laws of outward nature to bring out the result, we depend on the equally hidden laws of inward association. I initiate him into the art of this experimentation. I familiarize him with the use of all kinds of diagrams and devices for aiding the imagination. I show him just what part abstract thought has in the process—a quite subsidiary one.
Peirce added that he assigns his students "a large number and great variety of exercises in dealing with real facts" and that "the invention of these exercises is the thing for which I hope to be remembered, for I believe they are destined to exert no little influence in the future." In the years that followed, as Peirce used his exercise sets for other purposes, the package of exercises was broken up and dispersed. The small set that has been reassembled (sels. 9, 10, 13) is at best an indication of what Peirce was so proud of, as many of the exercises derive from other authors. Had Peirce’s students successfully worked their way through all of his lessons, they would likely have become the proficient reasoners he promised, but in the end no one ever finished the course. Peirce did carry on with a few students for a year or two, and later even tried to revive the course, but his lack of capital from the outset and his move to Milford in April thwarted any real chance for success.
Still, in the spring of 1887, prospects seemed good, though Peirce’s circumstances were becoming more and more difficult. New York was an expensive place to live and Peirce’s salary from the Survey was barely enough to maintain a satisfactory lifestyle. With enough paying students he would have welcomed separation from the Survey, but with only a handful he could not afford to resign. Unfortunately, his Survey work, now confined to the reduction of observation data—which in better times would have been handled by computing assistants—was extremely time-consuming, and severely limited the time he could spend answering letters and promoting his logic course. More disturbing, starting in September of 1886 a crisis had been brewing over the report on pendulum operations from the ill-fated Greely Expedition to Lady Franklin Bay in the Arctic, and Peirce was caught in the middle of it. 5 In 1881, then Lieutenant Adolphus Greely led an Army expedition of twenty-five men to the northeastern part of Ellesmere Island to establish a scientific station above the 81st parallel at Fort Conger off Lady Franklin Bay. Greely's party had been organized to participate in the first International Polar Year, an eleven-nation effort to advance earth science in the Arctic and Antarctic during 1882-83. The astronomer for Greely's party, Sergeant Edward Israel, had been specially trained by Peirce in the use of pendulums for gravity determinations, and for sixteen days in January 1882 he diligently swung Peirce Pendulum No. 1 in a specially constructed ice shelter. Greely's party met with disaster when supply ships failed to reach Fort Conger in 1882 and 1883, and when a navy vessel finally reached the retreating expedition about two hundred miles south of Lady Franklin Bay at Cape Sabine in June 1884, only seven men had survived and only six would make it home. Throughout the agonizing final winter, with starvation threatening his men, Greely took great pains to preserve the scientific data obtained at such a high price. Knowing that the heavy pendulum was a dangerous burden as his party retreated from Fort Conger to Cape Sabine, Greely had given his men the option of abandoning it, but they had declined. Fearing that his party's camp might be missed by the much hoped-for relief expedition, he sent a party on 23 October 1883 to a prominent point on an island a few miles south of Cape Sabine in Payer Harbor to cache the records. Peirce’s pendulum, sealed in its case, was erected as a towering marker over the cache (see woodcut on p. 219).
The rescue of the expedition made international headlines, and Greely became an instant celebrity. There was some initial concern that the tragedy might have resulted from poor judgment on his part, and it was rumored that the survivors had resorted to cannibalism, but Greely was quickly exonerated. However, discord over the cost of the expedition and rescue troubled President Arthur and Secretary of War Lincoln, and they remained cool to Greely and even used his disaster as an opportunity to argue against future federal support for dangerous scientific missions. Not until Cleveland was elected President would Greely be duly recognized for his achievement and promoted first to Captain in 1886 and then to Brigadier General in 1887. The initial controversy over his leadership and the attempt to use his misfortune as an argument against federal support for science made Greely very sensitive to any criticism of his party's achievements.
In his first dispatch following the rescue, Greely had stated with much satisfaction that his party had saved and brought back the records of the meteorological, tidal, astronomical, magnetic, and pendulum observations, and he mentioned proudly that he had brought back the pendulum. In the 19 September 1884 issue of Science, the President of the British Association for the Advancement of Science proclaimed that "nothing in the annals of scientific heroism exceeded the devotion of those hungry men in sticking to that ponderous piece of metal." In consequence of the criticism of his expedition, and the considerable attention given to the pendulum, Greely was determined to include Peirce’s account of the Ft. Conger pendulum observations in his official report. Yet by September 1886, over two years after Peirce had been given the pendulum records, and with everything else in hand, Greely was still waiting for the gravity results. Knowing that Superintendent Thorn feared bad publicity, Greely threatened to go to press without Peirce’s report: "It is needless for me to point out the comments which will be called forth in America and Europe, if these observations are wanting when the final report appears." 6 Responding as Greely hoped, Thorn put tremendous pressure on Peirce to turn in his report at once.
Thorn knew that Peirce had delayed his report because of some remaining uncertainties over the expansion coefficient for Pendulum No. 1 which he believed could not be resolved without taking No. 1 to a northern station, preferably St. Paul or Minneapolis, where it could be swung in the summer and again in the winter under extreme conditions as similar as possible to those at Ft. Conger. Peirce felt it his duty to turn Greely's hard-won data into the most significant results possible and he knew what that required. As early as April 1886, he had informed the Assistant in Charge of the Survey's Washington office, Benjamin A. Colonna, of his concerns and of his plan to swing the pendulum at a suitable northern location, and by September he had informed Superintendent Thorn directly. As the Coast Survey authority on pendulum operations, and given the importance of the Greely observations, Peirce probably expected his recommendation to be accepted without opposition, but he did not count on, nor perhaps even fully comprehend, the political pressures on Thorn. Peirce’s stubbornness, however justified from the standpoint of pure science, rankled Thorn, who threatened to take the matter entirely out of Peirce’s hands. Finally seeing the urgency of issuing the report, even if not fully adequate, Peirce reluctantly conceded: "You are aware that my judgment is averse to the publication of the Greely matter; but as you were plainly determined upon it, I thought it my duty to do all I possibly could to try to render that publication useful . . ." When Peirce wrote this on 22 March 1887 he added: "I have wasted more time upon this than I should have thought it worth while to do, except for my desire to make the best of this Greely publication. . . . I perceive you are becoming very impatient, and I will give up trying to perform the impossible, and send on the work as soon as I can."
Three weeks later Peirce submitted his report, but instead of settling things down it made matters worse. Although in muted terms, Peirce had included all of his criticisms and concerns. In accordance with Peirce’s instructions, after the pendulum at Ft. Conger had been swung for eight days, the knives had been removed and interchanged. But after that interchange, the periods of oscillation were noticeably different, too different to be accounted for, Peirce believed, by the contraction of the pendulum due to colder temperatures or by slippage of a knife, as suggested by one of Peirce’s past assistants, Henry Farquhar (see annotation 220.4), who, in the past, had frequently been assigned to assist Peirce. There was a remote possibility, Peirce suggested, that the change was the result of frost accumulation on the knives during the interchange, but he thought it really could not be satisfactorily explained and would detract from the usefulness of the results until further experiments could be made at a northern station. To make matters worse, he pointed out that the pendulum appeared to have lost between 10 and 15 grams of mass, 7 probably as a result of an accident during the difficult retreat from Ft. Conger to Cape Sabine. Such a loss of mass would explain a variation in the pendulum's period of oscillation after its return. In raising these concerns, it is clear that Peirce’s purpose was to present the Ft. Conger results in a way that made sense, and being fully aware of how often damage occurs to scientific equipment, especially in rough conditions, he had no idea his report would give offense. But Greely's high sensitivity to criticism blinded him to Peirce’s good intentions and he became furious. Thorn set the Survey office to work to diffuse the tension. Farquhar was asked to write a supplementary report to mitigate Peirce’s account and Greely added a memorandum (pp. 243-44) in which he fervently denied that any accident had happened to the pendulum. He went so far as to accuse Peirce of having given Sergeant Israel inadequate training and of failure to supply any written instructions, even though he had earlier praised Peirce for the care with which he had instructed Israel—care documented by Peirce’s detailed written instructions, which have survived and can be found with the papers that Greely brought back from Ft. Conger (see annotation 216.19).
When he saw Greely's memorandum, Peirce was dismayed that such offense had been taken, and he immediately submitted a conciliatory note to be printed with Greely's memorandum (pp. 244-45). In this note, Peirce stressed that he had no intention whatsoever of imputing any blame for what he considered to be normal occurrences under the circumstances, and he emphasized that Greely and Israel deserved nothing less than the highest honor for their "signally successful" gravity determination. He did refer, though, to "the only doubt which affects the result, namely, that which relates to the temperature-correction," but added that this doubt was destined to be resolved when further experiments could be made in the North. Greely's two-volume report, including Peirce’s Ft. Conger "Pendulum Observations" (sel. 30), finally appeared in the fall of 1888, and Peirce’s "Explanatory Note" was inserted to appear with Greely's "Memorandum." Greely was satisfied and wrote to Peirce on 30 November 1888 that he understood that no blame had been intended. He added: "I beg to assure you that I have always been impressed with your earnestness and zeal in connection with these observations, and I know that you were very decided in insisting upon the conditions under which the work should be done. I cannot well believe that any one should consider you as desirous of pulling down a house which has been substantially built with your hands; for to your assiduity, skill, and knowledge must be credited, as I have always understood, the latest and most important advances in the methods of application of pendulum observations." That brought to an end an unfortunate episode largely fueled by misunderstanding; but while Peirce’s relations with Greely seemed to have been mended, his relations with the Survey had suffered further damage.
As he grappled with the Ft. Conger pendulum results, Peirce continued working on his definitions for the Century Dictionary —before long his main concern. And, typically, from time to time other topics would catch his attention. In 1886, three members of the English Psychical Research Society, Edmund Gurney, Frederic Myers, and Frank Podmore, published a book which recounted hundreds of cases of the hallucination of the appearance of a person who would die or had died within twelve hours of their "appearance" and a scientific case was made for the authenticity of telepathic and apparitional phenomena. William James, a close friend of Gurney and a member of the English Psychical Research Society as well as of its American counterpart, gave the book, Phantasms of the Living, a very positive review in the January 1887 issue of Science. Peirce, who would have known of the book in any case because of his many acquaintances in the American branch of the Society (to which he never belonged), including his own brother Jem, must have been struck by James's praise for the book. Only two years earlier, Peirce had speculated (W5: sel. 24) that presumed telepathic phenomena were the result of faint sensations, and he had endorsed the field as worthy of further scientific study. So in early 1887, Peirce was working his way through the main argument of this huge book with his own review in mind—it would appear later in the year in the Proceedings of the American Society for Psychical Research (sel. 16) and trigger a controversy with Gurney that would continue for two years.
Probably in March, Peirce and a few other prominent American scientists were asked to contribute short articles to The Christian Register for a series on how science viewed belief in a future life. Peirce agreed to participate and drew material from his ongoing examination of Phantasms for his contribution (sel. 14). He wrote to his mother on 3 April 1887 that his work for his correspondence course was improving his writing style and that he hoped in a year or two to be "as good a writer as these men who write the editorials in the New York papers, who turn out so much good English and good sense." The little piece for the Register, published on 7 April, gave Peirce an opportunity not only to try out his developing style, but also to "announce" a few ideas that were growing more and more important for him and that would become signature doctrines. Among these were his ideas that the variety in the universe could not have come about by strict adherence to mechanical law and that there are no definite limits to human knowledge. According to Max Fisch, it is here that Peirce first made his case in print against the doctrine of necessity. 8 Peirce thought that although the evidence in favor of afterlife was not strong, it might be expected to become stronger. As to the "shades" who supposedly survive physical death, existing evidence could only bring Peirce to conclude that they were mere ghosts of their former selves—and so painfully solemn. Perhaps revealing more of his own circumstances than he intended, he wrote that were he suddenly to find himself "liberated from all the trials and responsibilities of this life, my probation over, and my destiny put beyond marring or making, I should . . . regard the situation as a stupendous frolic, should be at the summit of gayety, and should only be too glad to leave the vale of tears behind." He certainly would not "come mooning back . . . to cry over spilled milk."
Probably while he was working on his contribution for the "Science and Immortality" series, possibly slightly later, Peirce wrote a paper entitled "Logical Machines" (sel. 15) for the November inaugural issue of G. Stanley Hall's American Journal of Psychology. Peirce argued for the superiority of Allan Marquand's logic machine over that of Jevons, but he offered some improvements and suggested that it should be possible to construct a machine "which should work the logic of relations with a large number of terms." Peirce believed that the study of such machines was a good way to improve logic. In this paper Peirce did not mention his recent recommendation to Marquand to use electrical switching circuits for logical operations (W5:421-22), 9 but he did, in passing, make some interesting remarks about "the secret of all reasoning machines" and the appropriateness of calling such machines "reasoning machines," and then suggested that to some extent every machine is a reasoning machine—to the extent that they depend on "the objective reason embodied in the laws of nature." Peirce claimed that "reasoning machines" are destitute of originality and initiative: "it cannot find its own problems; . . . it cannot direct itself between different possible procedures." The absence of originality, however, is no defect for a machine: "we no more want an original machine, than a house-builder would want an original journeyman, or an American board of college trustees would hire an original professor"—a clear reference to himself.
It is not surprising that what we see of Peirce’s life mirrored in his writings from this period appears as troubled and somewhat embittered. He had been forced to leave Johns Hopkins and, though not without hope, saw no good prospect of an appointment at another university. The Coast Survey was in disarray and he knew that it was just a matter of time until his career there would come to an end. His one hope was his correspondence course. He felt sure it could succeed—but without the capital to begin his scheme at full strength it would have to grow to a critical mass before he could devote himself to it fully, and reaching that point would take time. Could he and Juliette survive in New York while they waited? On 3 April, Peirce wrote to his mother:
It seems to be pretty certain that there is going to be enough to live on from my lessons any way, even in New York. But I shall go into the country the first of May and economize a little; and can stay there next winter if necessary. The expenses have so far eaten largely into the profits, but I have made arrangements to reduce the cost of my advertising, and at the same time make it more effective. My clerks will get trained and will make the letters less costly, and the purchases of type-writers, etc. will cease, or nearly so, as I reach my maximum. For the next few months, this will be a heavy expense, but then I expect to retain the Coast Survey two, and perhaps three, months more. That gives me more than enough to pay for type-writers. I think I shall eventually make a handsome thing of this. At any rate, I shall make a living, and earn the everlasting gratitude of the country, when the effects of the training come to be seen. I have had an enormous quantity of extremely interesting letters from teachers, professors, lawyers, business men, etc. I am also getting numerous suggestions to invest money. But I have not yet been obliged to purchase a steam coupon-cutting machine.
Peirce’s spirits sound high but he must have been putting his best face on for his mother—in fact, during most of this period he was in emotional turmoil. He was under constant, often extreme, pressure from Thorn to submit reports, yet congressional budget cuts made it virtually impossible for him to receive sustained computing assistance, especially since he had moved out of Washington. There were some exceptions, but Peirce was left to his own devices most of the time. He thus confronted a mountain of data at the very time he found his powers as a mathematical computer to be weakening. A few years later, in December 1891, as he was about to resign, Peirce wrote to then Superintendent T. C. Mendenhall what amounted to a confession about his hidden struggle with his loss of computing proficiency.
My mind, as it seems to me, is generally sound and decidedly strong. But of late years, in a certain direction a singular weakness has been growing upon me; though I cannot but believe that with a good rest I should recover. When Thorn had been in about a year I think it was that I found I got all mixed up about my computations, and at first complained of it openly. Then, I began to see that it would injure me and kept quiet about it. We were constantly expecting that Mr. Thorn would go, and I was determined that when he did I would ask to be sent into the field. Then I came into the country and found myself better at first. Besides, I got upon hydrodynamics which did not affect me the same way. I worked very hard, and could find nobody who could give me much help. But my tendency to become confused about complicated computations increased, and was aggravated by having no aid. I became almost incapable of reading certain kinds of mathematics, though other kinds, much more difficult to most minds, afford me little difficulty. The more trouble I had, the less I liked to acknowledge it. So I temporized and got along as well as I could . . . (18 December 91)
It is easy to imagine Peirce’s frustration when Thorn pushed him beyond limits he was prepared to acknowledge. Peirce’s relations with Thorn grew acrimonious and they became impatient and sarcastic with each other. To make matters worse, Peirce imagined that there was some kind of conspiracy to get him out of the Survey. While this may have been a paranoid response, there is evidence that B. A. Colonna (who during Thorn's tenure 10 was officially in charge of the Survey's Washington office but unofficially acted as the de facto superintendent) was working behind the scenes to turn Thorn against Peirce. It was Colonna who had created a stir in the scientific community during the 1885 investigation of the Survey by describing Peirce’s gravity work as of "meager value" (see W5:xxix) and Peirce’s letters to Thorn frequently contain marginal notes added by Colonna, seemingly intended to dispose Thorn against him. For example, in the margin of a 30 September 1886 letter to Thorn in which Peirce outlined some of his concerns with the Greely data and asked for help with the computations, Colonna wrote: "It is plainly evident that if we depend on Peirce we get nothing. I would suggest a letter to him directing that he turn over to the office all the Greely records and any others that he may already have made bearing on them & that he do so at once." And when on 9 July 1887 Peirce sent in a few unpaid vouchers from his pendulum operations at Hoboken the previous year, Colonna sent this exasperated note to Thorn: "Mr. Peirce extended time and time again his allotment and still left these bills unpaid. Open with him again and where will you stop?" The simple fact is, there was bad blood between Peirce and Colonna, 11 and whatever his motives, Colonna did want Peirce out of the Survey: "Charles Peirce about crazes me. He has no system, no idea of order or business & with all his talent is a deadweight. I wish he could get a larger salary somewhere else and leave us. We could spare his talent for the sake of a better order." 12
More stressful than his career instability were his increasingly bad relations with his family and friends over his marriage to Juliette. Established society wanted no part of Juliette and even old friends, including Samuel P. Langley, withdrew from Peirce. Peirce’s Aunt Elisabeth (Lizzie), who owned the house his mother and brother Jem lived in, despised Juliette, and made it plain that she was not welcome in her home. Aunt Lizzie wrote to Peirce’s sister Helen after the death of Herbert's (Berts's) baby girl: "I had a little talk with Berts about Juliette & he feels about her just as I do. . . . It seems she is studying for the theater to learn how to act; it will be an easy lesson for her—though I don't see that there is much left for her to learn" (22 April 1886). She wrote later (4 July 1886): "I have many sad hours thinking of Charles. He did wrong to marry Zina—& he suffered for it—but he was young then. Now there is no excuse for him in tying himself to that miserable Juliette—whom we ought not & cannot receive. There is no question about it. She is, I feel sure, a very dangerous person—& our only course is to keep her at a distance." In January 1887, Peirce had a flare-up with Jem over Juliette. Peirce had written to Jem pleading with him to warm up to her:
If you had any discernment of human nature you would see that the worst thing you could do for me and the worst thing all round is to treat Juliette with any want of love & confidence. We have bad things to face in the near future, all of us; and you may be sure we had best stick together. That we can't do if you are going to be distrustful of Juliette. She burns under a sense of your injustice to her. Half our misery comes from that. (c. 20 January 1887)
Jem's reply was not conciliatory. He wrote that he had "no wish to enter on a disagreeable discussion," but he went on to say that he could not permit himself "to be called to account for sentiments & conduct to which I am driven by the hard stress of facts" (21 January 1887). He insinuated pointedly that Juliette had acted disloyally to Peirce during that very week. Peirce responded sharply: "As you insist on putting me into the position of choosing between you and my wife,—quite unnecessarily—of course I choose my wife. You thus get rid of a troublesome relative very neatly, & at a time when he is more troublesome than ever" (c. 22 January 1887). The fact was, however, that Peirce’s own feelings for Juliette were mixed. Though he had become completely committed to her, he was aware that she had already caused him much harm and he did not fully trust her. When he had written to Jem earlier in January about the plans for his correspondence course, he said plainly that he was afraid Juliette would somehow interfere: "She may intercept letters from pupils & break up correspondence. . . ." He added that Juliette would not permit him to have a clerk at their flat, nor have any woman work for him at all, and he revealed that he even suspected that Juliette was somehow to blame for his troubles with the Coast Survey. "Uncle Sam and Juliet [sic] are enough to drive me out of my wits." But his feelings for Juliette fluctuated wildly. He ended by asking Jem to burn the letter, "which is imprudent, because I love her devotedly."
As Peirce’s old social and family ties unraveled, he and Juliette began to associate with a more bohemian crowd—people like New York playwright and director Steele MacKaye and his wife Mary, writer and editor Titus Munson Coan, poet and stockbroker—and editor of the works of Edgar Allan Poe—Edmund Clarence Stedman, geologist and chemist Persifor Frazer, known for his atheism, and artists Albert Bierstadt, Alfred L. Brennen, and George B. Butler. 13 One of Juliette's New York friends, Mary Eno Pinchot, had a country estate in the Pocono Mountains just outside of Milford, Pennsylvania. Peirce and Juliette had visited Milford and were much attracted to the beauty of the surrounding countryside and, in particular, to the French community that had gathered there. The Peirces found that they were most easily accepted by people of French heritage. The need to economize, together with the attraction of an accepting community, convinced them to pull up stakes and move to Milford. It did not detract from this decision, as Joseph Brent has pointed out, 14 that the Pinchot family had great wealth and that they regularly entertained the likes of the Vanderbilts, Stuyvesants, Harrimans, and Belmonts. Here seemed to be an opportunity for Peirce and Juliette to enter a rich society even if not the society of Peirce’s heritage. In later years, Peirce remembered the time differently. In a draft of his 1908 paper, "A Neglected Argument for the Reality of God," (R 842), Peirce reminisced: "In 1887, when I had attained a standing among American scientific men sufficiently to satisfy a man of very little ambition, I retired to the wildest country of the Northern States, south of the Adirondacks and east of the Alleghanies, where I might have the least distraction from the study of logic." But though this may be what he came to value most highly about his retreat from city life, it is far from certain that this motive had anything to do with his decision to move to Pennsylvania.
The Peirces arrived in Milford on Thursday, 28 April 1887, and checked into the Hotel Fauchère. Within two weeks the Peirces had leased a house in Milford, characterized by Peirce’s mother as "luxurious quarters" (3 June 87), and proceeded to enter into the village life. Peirce joined the Episcopalian church and became friendly with the local clergy. 15 He and Juliette became frequent guests of the Pinchots at their Norman-style mansion they called "Grey Towers." Brent has described how they spent many afternoons and evenings at Grey Towers playing charades, capped with Peirce reading and reciting, and in September the Peirces "wrote, produced, directed, and acted" in a play given in the Pinchot's private theatre. 16
Although the move disrupted Peirce’s correspondence course and the preparation of his reports for the Coast Survey, it did not take him long to resume those efforts. The correspondence course would never achieve a critical mass and would gradually expire, but his Survey work would continue for another four and a half years. His official assignment at that time was to reduce the data from his post-1881 pendulum observations and produce publishable results, but his main interest would soon become the theory of the hydrodynamical effect of air on pendulum movement. Peirce also went back to work on his definitions for the Century Dictionary, and would spend the following three years working more intensively on his definitions than on anything else.
Peirce’s relations with his family deteriorated further after the move to Milford. Aunt Lizzie became even more vitriolic about Juliette. She wrote to Peirce’s sister: "I think that your mother blames me for the stand I take about Charles & Juliette. . . . We can not have them here at all. In fact I know Juliette enough from my own observation, that she would be a dreadful creature to have in the house. She is a liar & very artful, & she cares for nobody but herself, & she wd be worse than a rattle-snake in the house" (8 August 1887). She wrote of Juliette's alleged genius for acting that "she always has been on the stage & ought to be an adept by this time" but that "if she is a genius I fear it is a cracked one," and that "I utterly distrust her & hope I never see her again" (5 May and 9 June 1887). Even Peirce’s mother, who had alone seemed always to maintain a genuine concern in Juliette, seemed to turn against her. In August, Mrs. Peirce traveled to Newport with Jem after vaguely inviting Charles and Juliette to meet them, but Jem waited until it was too late—nine days into their visit—to write that they could come. When Charles learned of this, he was furious and wrote a scathing letter draft that he never sent:
It is best I should say once for all a few plain words which I shall not repeat concerning an expression in your last. You say you hope Juliette will let me come on to Cambridge. I wish Juliette would not urge me to go but would resent as I think she ought your insufferable and vulgar insolence. You insult me deeply in supposing or pretending to suppose I ever would go into that house. Whatever your object may have been in driving me to this decision, you have succeeded in that.Your inviting us to meet you and mother in Newport and then not letting us know till you had been there 9 days when mother writes that I can put any construction I like on her silence, confirms me in [the] decision self-respect ought to have brought me to long ago.I was deeply attached to you all, but you have all behaved ignobly & contemptibly, & I will pay up what I owe & be done with you. (22 Aug. 1887)
He did send a telegram that he immediately regretted sending and wrote to Jem to express his "sorrow and shame at having used an insulting expression." He promised that "As long as mother lives, at least, I want to have the best relations possible with those she loves" (21 Sept. 1887).
Peirce’s mother would not live for much longer. On 4 October, Peirce was called to her bedside and she died six days later. Unfortunately, the tensions toward Juliette, who accompanied Peirce to the funeral and stayed on with him as he helped settle affairs, did not let up during the period of mourning. On the 15th, Aunt Lizzie wrote to Helen: "I hope I shall hear today when Charles & Dulcinea are going. I hope today but this I cannot expect. I wish she was at the South Pole, the North being too much in the neighborhood. . . ." She wrote again on the 21st: "I do not hear any thing yet of Charles' going—I hope & trust they will go this week & never return." A few days later she could finally write: "Charles is going tomorrow & then I shall breathe freely. I am always afraid she will make an invasion. I feel quite sure that she has got Charles into her power—& she would like to get us all if she could. . . . However we need not be afraid of her if we can only keep her at a distance." When Peirce’s mother's estate was eventually settled about a year later, his share came to about $2000, including $1000 he had borrowed in 1885. He also got back some books he had given his mother, in particular a Leopold Shakespeare which had been dear to her. 17
The move from New York and his family troubles did not prevent Peirce from making some progress on the intellectual front. By mid-May 1887, he had finished his review of Phantasms of the Living, his first paper after arriving in Milford. Although Peirce did not believe that the postulation of telepathy and apparitions, Gurney's "ghosts," formed a good hypothesis for explaining the unusual phenomena recounted in Phantasms, that conviction was not why he devoted so much attention to that gigantic book. Gurney, Myers, and Podmore had put forward their results as a serious scientific study and had presumed to build their argument on the basis of probabilities, hoping to show that in an earlier investigation by Charles Richet the probability in favor of telepathic phenomena had been found to be too low. 18 The critical use of probability theory in the design of scientific experiments and the analysis of results was relatively new, although not for Peirce, who was an expert in two sciences that were exceptions, astronomy and geodesy. In the preceding decade Peirce had devoted much thought to extending the use of statistical reasoning to new sciences, and in the 1883-84 experiments with Jastrow, he had introduced the first modern randomized experimental design for psychology. 19 Peirce saw at once that the method of Gurney and his associates was inadequate to their task and that they had seriously misapplied the logic of probability. However well-intentioned, their work amounted to an attack on the logic of science, and Peirce could not let it go unanswered. It only made matters worse that William James had been impressed by the absurd claim made in Phantasms that the odds in favor of "ghosts" was about "a thousand billion trillion trillion trillions to one." 20 In the first paragraph of his "Criticism" (sel. 16), Peirce alluded to this claim— "I shall not cite these numbers, which captivate the ignorant. . . ."—and pointed out that "no human certitude reaches such figures as trillions, or even billions to one." Gurney, Myers, and Podmore had presented thirty-one cases 21 which they claimed established their hypothesis to this remarkable degree of certitude and Peirce’s aim was to show how their results were vitiated by inadequate sampling and control procedures; specifically, that in each of the thirty-one cases they had failed to meet one or more of sixteen conditions of an adequately designed experiment.
Peirce’s review was forwarded to Gurney for a reply to be published along with it. These papers, together with a rejoinder by Peirce probably written in the late summer or fall, appeared in the December 1887 issue of the Proceedings of the American Society for Psychical Research. In his review (sel. 16) Peirce’s criticism of the thirty-one cases was somewhat casual and perhaps slightly derisive, containing a number of inaccuracies and exaggerations that Gurney, in his lengthy "Remarks" (sel. 17), pounced on. He answered Peirce point for point, often with an impatience that matched Peirce’s swagger. He did admit that perhaps he and his colleagues fell "far short of Mr. Peirce’s standard in respect of caution, shrewdness of observation, and severity of logic," but he supposed that his deficiencies were not so great as to override the weight of the evidence. Peirce, stung a bit by some of Gurney's rebuttals, wrote a "Rejoinder" (sel. 18) almost as long as Gurney's "Remarks" and more technical and precise than his original criticism. He reiterated why he had felt the need to take a stand against Gurney, namely, that "to admit the existence of a principle, of which we certainly only meet with manifestations in very exceptional observations, is to rashly set the prosperity of scientific progress at hazard." He then answered all of Gurney's rebuttals and attempted to show that once the suspicious or problematic cases were weeded out there really was no "weight of evidence" at all. Peirce praised Gurney for adopting a statistical method "with a view of putting this question to rest," but his badly designed study "leaves the question where he found it." In response to Gurney's claim that any bias he might have in favor of the supernatural was no greater than Peirce’s bias against it, Peirce agreed, but he added that "a bias against a new and confounding theory is no more than conservative caution; while a bias in favor of such a theory is destructive of sound judgment." Gurney set about answering Peirce’s "Rejoinder," but had not finished his remarks when, in 1888, he apparently took his own life. It is thought that the impetus for his apparent suicide was the revelation that his assistant, George Albert Smith, had manufactured evidence (annotation 61.23). Gurney's final but unfinished answer to Peirce appeared posthumously in 1889 as "Remarks on Mr. Peirce’s Rejoinder," with a concluding "Postscript" by Myers (sel. 19). In his final "Remarks" Gurney wanted to make it clear that he was really not an advocate for the supernatural and that, in fact, he agreed with Peirce "in professing `a legitimate and well-founded prejudice against the supernatural.'" The entire controversy had been acrimonious, with both parties sometimes verging on the scornful. Ian Hacking says "It is Peirce at his crankiest (but none the less sound for that)," and he suspects "that many of the Boston skeptics were egging him on." 22 On his side, Gurney had the resources and encouragement of the Psychical Research Society behind him, along with his co-editors and assistants. But, all in all, one senses that the disputants did not lose respect for each other and even understood that they were in a curious way working together in an effort to advance human knowledge. About a dozen years later, when Peirce revisited this subject for a paper he was writing on "Telepathy and Perception," he reminisced: "I had a somewhat prolonged controversy with Edmund Gurney which was only interrupted by his death; and this brought me into fine touch with the spirit of the man. I was most strongly impressed with the purity of his devotion to truth" (CP 7.612).
After returning to Milford in October, following his mother's funeral, Peirce finished the year working on the theory of hydrodynamics, concerned with the effects on pendulums of the viscosity of air, and he worked on other matters related to his Coast Survey investigations, including his postponed report on the construction of a practical standard of length calibrated against a specified wave length of sodium light (W4:269-98). Peirce was probably stimulated to resume that work by three papers on wavelengths that appeared in 1887, one of them a study by Michelson and Morley precisely on the point of Peirce’s own research. Michelson and Morley's paper, and the others by Louis Bell and Henry Rowland, made reference to Peirce’s work. 23 Peirce also resumed work on his "Guess" and continued to write his definitions for the Century Dictionary. Possibly in connection with his dictionary work or his study of hydrodynamics, or his interest in mathematical pedagogy, and stimulated by an 1887 article in the Journal für die reine und angewandte Mathematik, 24 Peirce began a systematic study of curves that he would carry on for at least two more years (see sel. 42; also see c.1888.4 and 1889.3, 20-22 in the Chronological Catalog). Apparently in response to an invitation from Peirce to join in this study, Survey computer and occasional aid to Peirce, Allan Risteen, replied on 4 August: "It has often occurred to me that a collection ought to be made of these properties that are common to all curves of given kinds—say, closed curves—and that perhaps the close examination of such a set of general propositions might lead to others equally general, so that after a time we should have a general geometry in the truest sense." Sometime during the year Peirce also returned to his work on the theory of number and applied quantification theory to his 1881 axiomatization (sels. 20 and 21). 25 It is noteworthy that in "Logic of Number" (sel. 21), Peirce gives a technical definition of the "hereditary character" for number that brings to mind Frege's "hereditary property" (see annotation 156.11), but Peirce’s regrettable inattention to Frege, probably because of Schröder's dismissal of him, 26 argues that Peirce’s innovations arose from an independent course of thought. It is not definite when or how Peirce’s interest in number theory was rekindled; perhaps it was in connection with his study of number for his Century definition. A few years later, in 1896, he would present a lecture on number to the mathematics department at Bryn Mawr College (probably R 25), and number theory would periodically occupy him for the rest of his days.
In the latter months of 1887, Peirce began a correspondence with Francis C. Russell, a Chicago attorney who had taken a sudden interest in Peirce’s logic. Russell soon became something of a disciple of Peirce and, after he became associated with the Open Court Press, was instrumental in paving the way for Peirce to publish in The Monist. Peirce also resumed correspondence with William James, writing to him in October about his "admirable work on Space." 27 This was Peirce’s first letter to James after moving to Milford, and it may have been the first in two years—since his letter of October 1885 in which he had mentioned to James that he was working on "something very vast . . . an attempt to explain the laws of nature . . . to trace them to their origin & to predict new laws by the laws of the laws of nature." Then Peirce had been at the seminal stage of what would become the systematic metaphysics of his "A Guess at the Riddle," and not much later, his Monist metaphysical series. By October 1887, Peirce had penetrated much deeper into his "vast" undertaking, and he had been working through some of the same issues addressed by James in his article on space. After telling James how much he had learned, Peirce expressed some reservations: "I fancy that all which is present to consciousness is sensation & nothing assignable is a first sensation." He was not ready to admit "that size is so nearly a primary sensation as red or blue." Peirce suggested that "objective space" might be "built up" by a synthesis of fragmentary spaces and speculated that in the same way "objective time" might be built up by a synthesis of fragmentary times. Peirce concluded his letter by remarking that James had apparently not seen "Mayer's argument against Helmholtz's theory of audition."
Perhaps Peirce’s most intellectually stimulating correspondent of the time was Alfred Bray Kempe who, in November 1886, had sent him an inscribed copy of his recently published "Memoir on the Theory of Mathematical Form." 28 Peirce may have first learned of Kempe in July 1879, when it had been reported in Nature that he had proved the four-color conjecture that for any map only four colors are required to avoid having a boundary separating areas of the same color. Peirce seems to have had pre-publication access to Kempe's paper, which had been submitted to J. J. Sylvester for publication in the Johns Hopkins American Journal of Mathematics, and in 1880, before Kempe's paper appeared, Peirce offered some improvements on Kempe's method. 29 But it was Kempe's 1886 "Memoir" that would have a profound impact on Peirce, whose expertise in the logic of relations and interest in spatial logics enabled him immediately to see the genius of Kempe's graphical approach to relations. In order to exhibit essential forms, Kempe had introduced a graphical notation of spots and lines modeled on chemical diagrams, and this notation would play an important role in Peirce’s innovation of his Existential Graphs (EG). 30 On 17 January 1887, after carefully reading Kempe's memoir and making a list of new terms that he thought might be included in the Century Dictionary, Peirce wrote to Kempe with some suggestions that led Kempe to make revisions which he credited to Peirce. 31 In January of 1889 Peirce would return to Kempe's "Memoir" and still find it "so difficult that I was at work on it all day every day for about three weeks" (RL 80:105). Kempe's influence can be found in Peirce’s correspondence course exercises (sel. 9), especially those on relational graphs, and in the 1889 paper, "Mathematical Monads" (sel. 34), and in many other writings. In R 714 (1889.4), his fragmentary "Notes on Kempe's Paper on Mathematical Forms," Peirce even introduced lines to stand for individuals, an important move in the direction of EG.
The year 1888 began on a positive note for Peirce. On 1 January, President Cleveland appointed him to the Assay Commission, charged with testing coins from different U.S. mints for fineness and weight. Peirce served on two committees for the Commission, the Committee on Counting and the Committee on Weighing, and was a signatory for the final reports, signed on 10 February in Philadelphia. On 13 January Peirce and Juliette went to New York to see Steele MacKaye's new play, "Paul Kauvar," which had opened to acclaim on Christmas Eve. Mary MacKaye had sent them tickets. The Peirces continued to be frequent guests of the Pinchots, mingling with their well-heeled friends, and they had successfully entered into village life in Milford.
On 4 February, Peirce’s Aunt Lizzie died in the family home in Cambridge. Jem wrote in her obituary that she had been "a woman of remarkable character & intelligence" but that she had been "very singular, almost eccentric" and that her "greatest real fault was a certain streak of jealousy which she could not always conquer." He said that she had been devoted to reading, "especially to German literature & above all to Goethe, whom she esteemed the paragon of geniuses and of men." In fact she had held virtually the same opinion of her brother, Benjamin, to whom, as Jem put it, she had been "devotedly attached." Aunt Lizzie's funeral was held on 8 February and Peirce attended, but it is not likely that Juliette was with him. Aunt Lizzie's estate was divided among Benjamin's children and Peirce’s share came to about $5000.
Peirce’s inheritance, from Aunt Lizzie and from his mother, created the possibility for a life in Milford that would otherwise have been impossible. Even though Peirce still held out hope that he could make a success of his correspondence course, it was hardly lucrative nor likely to be so any time soon, and his combined income from the Survey and from the Century Company was quite inadequate to the life he and Juliette had assumed in Milford—with its socializing in the Pinchot circle and with frequent trips back to New York. And, of course, Peirce’s income from the Coast Survey was tenuous at best. To make matters more difficult, there were few suitable homes available for rent in Milford. When at the end of their first year the lease expired on their first house, it seemed that there was no place to go and that they would have to leave Milford. On 26 April a note appeared in the Port Jervis Evening Gazette (taken from Milford News ): "We fear that we are about to lose Prof. Charles A. Pierce [sic] and his excellent lady because of their inability to secure a suitable residence for the coming year." At the last minute Peirce did find a house to rent, the Scheinmee Homestead on Broad Street, but his inheritance made it possible to consider something more permanent. On 10 May, the Peirces bought a farm about two miles northeast of Milford in the direction of Port Jervis. They paid $1000 for the 130 acres on the Delaware River, which included a parcel called "Wanda Farm" that had been the homestead property of John T. Quick, one of the colorful early settlers in the area, and another parcel known as the "Quick Saw Mill Property." The property as a whole was called "Quicktown." Altogether, there were two houses, two barns, a large ice-house, a sawmill, and some other outbuildings. The farmhouse on Wanda Farm, built in 1854, was the main house and the one the Peirces would begin renovating in January 1889 with the aim of turning it into a magnificent resort that could accommodate summer guests and perhaps even a residential school of philosophy. But on 10 May, when the Peirces bought Quicktown, there was an understanding that they would not move in immediately and that some members of the Quick family could continue living in the main house for a period of time. That understanding would lead to complications later in the year, and descendants of the Quicks would come to believe that they had lost their property to the Peirces by some trick. 32
It is hard to tell how Peirce divided his time in 1888, but as the year got underway it seems certain that his intellectual work was mainly devoted to three efforts: to his Coast Survey reports, to his definitions for the Century Dictionary, and to the articulation of a system of thought founded on his categories and his evolutionary metaphysics. After Peirce submitted his report on the pendulum work at Fort Conger, he turned his attention to working up results from the considerable unreduced records of the gravity work he had carried out during the preceding five years, and some from even earlier. It was becoming more and more difficult for Peirce to sustain the mental focus and intensity required for the complex calculations that typified these reductions and he persistently tried to convince Superintendent Thorn that he needed assistance with the computations. Early in April Thorn finally agreed to assign Allan Risteen to work with Peirce on a temporary basis. Risteen and his wife moved to Milford and probably stayed with the Peirces until sometime in July. During those months it is likely that the reduction of data from gravity determinations was a constant in Peirce’s daily routine. But the fact that Risteen was there to help with the reductions probably allowed Peirce to work more on the related hydrodynamical theory, and it also freed him to spend more time on the Century Dictionary. Although Peirce had been working on definitions for at least five years, he was just beginning his most sustained and concentrated effort. Definitions were now being set in galleys and there was no choice but to turn considerable attention to that work. When the local newspaper had printed the notice that Milford might lose Peirce, it noted that he was engaged "in compiling a dictionary to be issued by the Century Company of N.Y." Clearly, Peirce’s lexicographic work was a prominent part of his life at that time.
The third undertaking that must have occupied Peirce a great deal as 1888 got underway was his philosophical system building. Sometime after moving to Milford, probably after his mother died, Peirce resumed work on his book, "One, Two, Three" (W5: sels. 47-50, but see also 35 and 36), rechristened as "A Guess at the Riddle" (sels. 22-28). It had been over three years since he had begun articulating his "evolutionary speculation" which by 20 August 1886, as he wrote Holden, had become "a great working hypothesis of science" (W5:xxxix). Peirce’s "speculation," his "guess," was that because of an "original, elemental, tendency of things to acquire determinate properties, to take habits" the universe itself has evolved from a state of "all but pure chance" to "the present almost exact conformity to law." Peirce had come to conceive of the grand cosmic history of the universe as of a kind with the evolutionary growth of biological systems.
What led Peirce to these cosmological speculations at that time can only be surmised. Although it is clear that many of the roots of Peirce’s grand idea ran deep into the earliest layers of his thought, it does seem that after his marriage to Juliette in 1883, and after he found out that his career at Johns Hopkins had been lost, he became decidedly focused on the riddle of the universe. 33 In his outline of how the argument of his book had developed (sel. 23, pp.175-176), he noted that after he had turned his illuminating categories to "the domain of natural selection," he had been "irresistibly carried on to speculations concerning physics": "One bold saltus landed me in a garden of fruitful and beautiful suggestions. . . ." That "bold saltus" may have been the "guess" itself, perhaps as expressed in his January 1884 "Design and Chance" lecture to the Johns Hopkins Metaphysical Club: "Now I will suppose that all known laws are due to chance and repose upon others far less rigid themselves due to chance and so on in an infinite regress . . . and in this way we see the possibility of an indefinite approximation toward a complete explanation of nature. . . . May not the laws of physics be habits gradually acquired by systems." For three or four years following his Metaphysical Club lecture, Peirce roamed in his Epicurean "garden of fruitful and beautiful suggestions":—his "One, Two, Three" writings of 1885-86 were part of that exploration. By the fall of 1887, as he began writing "A Guess at the Riddle," Peirce’s initial exploration had worked itself out and he had started looking for further implications or illuminations of his guess for sociology and theology. 34 The final two chapters, projected but probably never written, were to be expositions of the triad in those two subjects.
Another possibility is that the "bold saltus" was the "leap" he took, probably in the summer of 1885, from his growing understanding of the usefulness of his categories for logic to the speculation that they provided the key to a rich and unified system of science. By fall 1885 at the latest, he could show how "the whole organism of logic may be mentally evolved from the three conceptions of first, second, and third." He would conclude that "if these three conceptions enter as we find they do as elements of all conceptions connected with reasoning, they must be virtually in the mind when reasoning first commences" and he would add that "in that sense, they must be innate ideas" and "there must be in consciousness three faculties corresponding to these three categories" (W5:245) which, in turn, "must be capable of a physiological explanation from three fundamental properties of the nervous system" (W5:247). It was Peirce’s conjecture that his categories, firstness, secondness, and thirdness, or perhaps even the underlying conceptions "one," "two," and "three," were the building blocks for a vast, integrated system of knowledge, that led him by mid-1886 to turn the evolutionary speculation of his "Design and Chance" lecture into his guess at the riddle of the universe, namely, that the universe may be understood as a process in which chance brings forth first, or original, events, which, because of an inherent tendency "to acquire determinate properties, to take habits," become more and more systematic and law governed. The evolving law produces seconds and the tendency to take habits, which generates law, is the third "or mediating element" between firsts and seconds (W5:293). By early 1888, when he sketched chapter seven for "A Guess at the Riddle" (sel. 28), he had refined his guess to this succinct statement: "three elements are active in the world, first, chance; second, law; and third, habit-taking."
The main thrust of "A Guess at the Riddle" was an exploration of the fecundity of Peirce’s categories for different sciences and the construction of a unifying structure of fundamental conceptions. In each of the extant chapter sketches Peirce used his categories as a device for rethinking and refining old ideas. For example, in chapter 1, "Trichotomy" (sel. 23), he showed how ubiquitous firstness, secondness, and thirdness are by connecting them with common conceptions such as spontaneity, result, and bridge, or beginning, end, and process. But why stop with one, two, three, he asked. Because, he said, "any number, however large, can be built out of triads; and consequently no idea can be involved in such a number radically different from the idea of three." He used a model of a road with three-way forkings to demonstrate his point. Peirce’s analysis of degenerate categories revealed that there are two distinct varieties of secondness, one internal and one external. It may have been Hegel's failure to understand this, Peirce suggested, that led him to commit "the trifling oversight of forgetting that there is a real world with real actions and reactions."
Chapter 2, "The Triad in Reasoning," was probably never written, unless Peirce intended "One, Two, Three: Fundamental Categories of Thought and of Nature" (W5: sel. 35) to be a preliminary draft, or at least a precursor of it. However, it is very suggestively outlined in the "Contents" (sel. 22) with particular reference to Peirce’s 1885 paper in the American Journal of Mathematics (W5: sel. 30) where it was stressed that for "a perfect system of logical notation" it is necessary to employ three kinds of signs: icons, indices, and tokens (what would later be called "symbols"). Immediately following "A Guess at the Riddle" is a short selection on Steele MacKaye's theory of dramatic expression entitled "Trichotomic" (sel. 29). This paper, probably written for oral presentation during the early part of 1888 while "Guess" was in progress, effectively though very briefly summarizes four of its chapters (1, 2, 4, and 5). The discussion of signs complements the outline given in the "Contents" (sel. 22), and, together, they give a good idea of what Peirce had in mind for Chapter 2.
Chapter 3, "The Triad in Metaphysics," (sel. 24) is only a fragment of a sketch of what Peirce planned to write, but it strongly indicates that Peirce viewed his cosmology in relation to Greek thought, particularly pre-Socratic philosophy. His plan was to "run over all the conceptions that played an important part in the pre-Socratic philosophy and see how far they can be expressed in terms of one, two, three." He did not get far, but he pointed out that the Greek arche, the "primal matter out of which the world [was] made," was quintessentially his first. A fragmentary list of pre-Socratic doctrines (annotation 181.4-5), probably to be used as a source-list for Chapter 3, indicates further some of what Peirce might have included had he completed that chapter. For example, the thirtieth item on this list is a quotation of Parmenides taken from Plato's Symposium (178b): "He devised Love the very first of all the gods." Peirce then remarked: "But this doctrine was of course infinitely more ancient. Hesiod, quoted by Plato in the same place in the Symposium, puts Chaos first, earth second, and love third."
In Chapter 4, "The Triad in Psychology" (sel. 25), the application of his categories revealed to Peirce that there are "three radically different elements of consciousness": immediate feeling (consciousness of the first), polar sense (consciousness of the second), and synthetical consciousness (consciousness of a third or medium). In Chapter 5, "The Triad in Physiology" (sel. 26), Peirce used his categories to find a threefold division in the physiology of the nervous system that would account for the three kinds of consciousness. As though anticipating that he might be accused of reductionism, Peirce wrote: "No materialism is implied in this, further than that intimate dependence of the action of the mind upon the body, which every student of the subject must and does now acknowledge" (p. 188). Peirce concluded that three fundamental functions of the nervous system were, "1st, the excitation of cells, 2nd, the transfer of excitation over fibers, 3rd, the fixing of definite tendencies under the influence of habit," and he considered further whether these functions were "due to three properties of the protoplasm or life-slime itself " (p. 193).
In Chapter 6, "The Triad in Biological Development" (sel. 27), Peirce’s examination led him to three principle factors in the process of natural selection: "1st, the principle of individual variation or sporting; 2nd, the principle of hereditary transmission, which wars with the first principle; and 3rd, the principle of the elimination of unfavorable characters." Peirce concluded that the principle of sporting is a principle of chance corresponding to his category of first, the principle of heredity is a principle of compulsion corresponding to his category of second, and the principle of the elimination of unfavorable characters is a principle of generalization corresponding to some extent to his category of third. But he acknowledged that the correspondence of the main principles of natural selection with his categories was not perfect and he speculated that "its imperfection may be the imperfection of the theory of development" (p. 202).
In Chapter 7, "The Triad in Physics" (sel. 28), the last extant chapter sketch for the book, Peirce delivered his guess that there are three active elements in the universe: "first, chance; second, law; and third, habit-taking." Finally, we know from the "Contents" that Peirce intended to finish with chapters on sociology and theology, but there is not much indication of what fundamental triads he expected to find. He does note under "The triad in sociology" that "consciousness is a sort of public spirit among the nerve-cells" and under "The triad in theology," that "faith requires us to be materialists without flinching," but this only gives a little of the flavor of what Peirce might have written. It is true, though, that in his first chapter, "Trichotomy," when he was discussing "absolutes" in cosmology, he alluded to the theological triad: "The starting-point of the universe, God the Creator, is the Absolute First; the terminus of the universe, God completely revealed, is the Absolute Second; every state of the universe at a measurable point of time is the Third" (sel. 23, pp. 173-174). Although Peirce tended to identify the third with representation, here we find, that in leading from first to last (second), third is process. Insofar as Christian theology holds that the universe is developing from "God the Creator" toward "God completely revealed," Peirce regarded it as an evolutionary doctrine. Perhaps this is the approach he wanted to develop in Chapter 9.
Peirce had a remarkable confidence in the importance of "A Guess at the Riddle." He was convinced that not only was it "destined to play a great part in the future," as he wrote to Holden (W4:xxxix), but that he was inaugurating a new philosophy which, like the earlier system of Aristotle, was so comprehensive that "for a long time to come, the entire work of human reason . . . shall appear as the filling up of its details" (sel. 23, pp. 168-169). He envisioned his new system as a "philosophical edifice," constructed on a deep and massive foundation, which unlike the Schelling-Hegel mansion—found to be uninhabitable almost immediately upon opening its doors—would be the principal habitat of philosophers long into the future. But Peirce’s book was never published, nor even completed, and even though he managed to get some of his architectonic ideas into print in his 1891-93 Monist series, he remained virtually the only inhabitant of the "Peirce mansion" during his own lifetime. After May 1888, when Peirce and Juliette purchased the house that would become Arisbe, Peirce would become preoccupied with architectural renovations. Chapter 1 of Peirce’s "Guess" (sel. 23), which was written out of order, may have been composed about the time Peirce began planning the renovation of his country house—when sound architectural structures became a matter of immediate practical importance for him. It is lamentable that Peirce would never finish either of his mansions and that, in their different ways, they would trammel him.
The evidence for when the Peirces moved to Wanda Farm and into their new house is inconclusive as it stands. By early June Peirce was using "Westfall Township," where his new estate was located, as his return address, and by July he was using the name "Quicktown." In an 8 June letter to Thorn, Peirce remarked that "on leaving Milford" he had lost his local clerk and on 2 July he said that his "movings" had taken five days. Yet as late as November he and Juliette stayed for a few weeks in a hotel in Milford while they dealt with legal issues pertaining to the eviction of the Quicks, which finally took place on 18 December. Probably the Peirces had moved to Quicktown shortly after they purchased it and occupied the secondary house, or some portion of the Quick house until the difficulties with the Quick's continuing occupancy became acute, but so far nothing conclusive has come to light. In any case, it was not until January 1889 that the Peirces finally moved fully into the main house and began rebuilding it to suit their purposes.
Wherever Peirce was residing during the second half of 1888, it is certain that his new estate was much on his mind. Except for the legal difficulties that arose concerning the Quick family, Quicktown was a place of promise for Peirce, a chance to make a good life for Juliette and himself. Together they must have spent many hours making plans and thinking about the hopeful future that now seemed within their grasp. Peirce tried to keep his Coast Survey work on track but without much success. He did manage on 10 August to send in a new paper on the mean figure of the earth, expanding on his previous paper of 1881 (W4:529-34), but Thorn, suspecting that it was somehow a ploy to ease the pressure he had been exerting on Peirce to complete his major gravity report, had it evaluated by Schott who returned an indecisive verdict. Schott made a vague insinuation that Peirce may have made some unattributed use of similar results of F. R. Helmert— "whose work came under the author's notice while writing his report"—and recommended that work on the earth's shape should be kept separate from "regular pendulum matter" in any case. Of course, for Peirce, determining the shape of the earth was the principal goal of his geodetic labors, and it was hardly beside the point to keep his gravity researches integrated with their ultimate purpose. But Peirce’s paper (which has not been located) was not published, although it was probably the source for the results that Peirce used in his definition of "Earth" for the Century Dictionary. Peirce’s work on the earth's figure and on its compression would continue to be mentioned in his monthly reports.
The texture of Peirce’s life can only be painted in pale outline in an introduction such as this one in which the aim is to provide a context for and a sketch of the intellectual development that gave birth to the writings in this volume. A more complete account of 1888 would describe more fully Peirce’s family relations, especially concerning the settlement of his mother's and aunt's estates, and would say more about his and Juliette's social and domestic lives. It would also say more about some of the correspondents who have been passed over in silence, and about some unmentioned incidents and flare-ups with the Survey's Washington office and scientific activities that have been left out—and, of course, there would be more about Peirce’s friends and colleagues and external matters that affected his life and thought. Chapter three of Joseph Brent's Charles Sanders Peirce: A Life should be consulted for a more complete account of these matters. Perhaps the main thing still to be said about the last half of 1888 is that Juliette's health took a turn for the worse and she would sometimes stay in New York, perhaps to be near New York physicians or because of the unsettled living conditions in Quicktown. Her health had always been worrisome for Peirce, but beginning in the spring of 1889 it would become a major concern.
On Thanksgiving Day, 29 November, Peirce wrote a newsy letter to his brother Jem. He thanked Jem for a remittance toward his inheritance and for the explanation of "fleflexnode" which "went straight into the dictionary." He said he had been "much occupied with small but pressing matters," and mentioned in particular the lawsuit concerning the eviction of the Quicks. He told Jem he was taking Juliette to New York on the following day and would return to the farm by himself. He reported that "Mrs. Pinchot wants us to change the name Quicktown, but I dont know that I agree with her. It is the name we found & `Tom Quick' is rather a romantic figure in the history of the valley"—the following year a monument to Tom Quick was erected in Milford to mark the one hundred and fifty-sixth anniversary of its settlement. Peirce told Jem that if he was reading novels he should get Le Capitaine Fracasse by Gautier. "For my part I read little literature & I find serious novels dull. I am loitering through Pepys again, & have been reading Sidney's Arcadia, Dr. Dee's preface to Euclid, Thirion's History of Arithmetic, Browning, Shelley, Keats, Wordsworth, Montaigne (of which I have an old French copy), Mémoires de Casanova, Our Mutual Friend, some old Arithmetic & other old books." He finished by remarking that the dictionary was coming along quickly. This letter gives a nice sense of the tone of Peirce’s life as the year was winding down. The final weeks of 1888 were dominated by the prospect of finally having full occupancy of the Quick house and plans for its renovation.
Peirce woke up at about 7:30 a.m. on New Year's Day, 1889, at Quinn's Halfway House, near Quicktown, from which he and Juliette would direct preparations for their move into their new house. He divided his day in a way that modeled how he would spend his time during the coming year. He devoted the morning to philosophy, in particular, to starting a new book, "Reflections on the Logic of Science" (sel. 31). After lunch he and Juliette drove to Port Jervis in their carriage to see a carpenter about an addition to the house. In later years, when Henry S. Leonard traveled from Harvard to interview elderly Milford residents about Peirces life, Mrs. Robert G. Barkley recalled that Peirce "drove a Phaeton with a white horse and gently waved a whip as he drove along." 35 Upon leaving Port Jervis, the Peirces crossed back into Pennsylvania to the village of Metamoras where they saw a second carpenter. After dinner that evening, Peirce and Juliette worked on accounts—Peirce noted in his diary that "there was some disagreement." Later he turned to galley proofs for the Century Dictionary, which he noted had reached "game," and to his overdue Coast Survey reports—at least he recorded these tasks in his diary for 1 January.
A few days later the reconstruction of the Quick house was underway and, although more or less completed stages would be reached, remodeling would continue with varying degrees of intensity and disruption for the rest of Peirce’s life, and even afterwards under Juliette's direction. Their home would become their prison in the way that Peirce’s philosophical mansion would imprison him, catching him up in a vision he could not resist but causing him much suffering as he steadfastly struggled against insurmountable odds to achieve it. But as 1889 lay before him, there was good reason to suppose that his hopes for his estate, as well as for his philosophy, would be realized. He could not then know what a great struggle he would endure trying to build these parallel edifices. Leonard recorded some anecdotes that give an idea of how this process appeared from the outside. Miss May Westbrook remembered: "When the Peirces built their house they built around an original house on the property. Mr. and Mrs. Peirce sometimes quarreled. Once when I was at their house for dinner the quarrel was violent. I don't know what it was about because they talked in French. Mrs. Peirce was an unreasonable person." Miss Westbrook noted that whenever she visited, Peirce was always in his study except for meals, but she added that when Juliette was in Europe, Peirce "took one meal a day here with mother. He was very pleasant. Mrs. Peirce sometimes spoke well of him and sometimes not." Gifford Pinchot also talked with Leonard about the Peirces' reconstruction project: "The alterations were of an absurd character. The attempt was to make the house irresistible as an Inn or a Gentleman's Estate. Mrs. Peirce had two passions: devotion to Peirce and interest in land. In the latter respect she showed a characteristic common among French peasants. Peirce was extremely impractical. He submitted to her plans for alterations in the house loyally and cheerfully, living in one room while all the others were in a turmoil with carpenters." Pinchot remembered how in 1887 and 1888 he had discussed forestry with Peirce and that those discussions had been instrumental in his decision to study forestry in Germany. Pinchot went on to become Theodore Roosevelt's Chief Forester and would play a large role in establishing the National Park System in the United States. He also recalled that it was Peirce who had calculated the settings for a sundial built into the stone front of Grey Towers, "so that it gave exact normal time for the longitude and latitude" and that he "calculated the true North and South that were marked in the sidewalk in front of the house." These markings are still visible today.
The book Peirce started writing on 1 January (sel. 31), might have been an outgrowth of Chapter VII of Peirce’s "A Guess at the Riddle," where he had made a number of the same observations he now planned to examine in detail—for example, that in order to have any hope of making progress in physics, we cannot simply work through one hypothesis after another without some hint to guide our initial choices. Peirce wanted to set out in detail the logic of science that supported his guess and that would recommend it as the hypothesis to guide physics. It may be that Peirce intended "Reflections" to be his "Illustrations of the Logic of Science" (W3:242-74) brought up to date. It is interesting that on the following day, 2 January, Francis Russell wrote to Peirce that "when your `Illustrations of the Logic of Science' came out the papers initiated in me a new era in my mental history and I am one of a necessary many who recognize in you a master to be followed." Russell then asked Peirce if he had changed his views since the "Illustrations." Peirce replied on the 8th, "Suffice it to say that I have not given up any of the more fundamental of my younger opinions so far as I recollect them, but am perhaps more sceptical & materialistic."
Peirce did not get very far with "Reflections." He began the second chapter with a discussion of the doctrine of chances but soon decided that a prior discussion of mathematics was needed. On 9 January he wrote a few paragraphs of a new draft of Chapter 2 and continued it on the 17th, but that was the end of it. On that day he began working on a mathematical paper, "Note on the Analytical Representation of Space as a Section of Higher Dimensional Space" (sel. 32), elaborating on a proof he had just sent to Simon Newcomb with the hope, soon dashed by Newcomb, that it would be published in the American Journal of Mathematics. It may have been Peirce’s interest in the mathematical foundations of the logic of science that caught him up in new mathematical investigations, or it may have been his work on hydrodynamics, but he continued working on mathematical topics throughout January and there are a number of other 1889 selections that may have been composed around that time. These include "Ordinal Geometry" (sel. 33), "Mathematical Monads" (sel. 34), "On a Geometrical Notation" (sel. 38), "On the Number of Forms of Sets" (sel. 39), "The Formal Classification of Relations" (sel. 40), "Dual Relatives" (sel. 41), and "Notes on Geometry of Plane Curves without Imaginaries" (sel. 42). Some of these papers, perhaps especially selection 34, and also the mathematical chapter of selection 31, may have been inspired by Peirce’s January study of Kempe's paper on mathematical forms, and others may have been outgrowths of his work on mathematical definitions for the Century or his correspondence with mathematicians such as Alfred Mayer and his own brother Jem.
Peirce’s enthusiasm for what was coming to pass in Quicktown was dampened by a continuing decline in Juliette's health. His diary reveals his growing concern. On 3 January he noted that "Juliette weighs 104 with thick clothes & heavy shawl" and on the 6th he wrote: "Much alarmed about Juliette's health. She spits so much blood. Juliette getting quite ill. If I should lose her, I would not survive her. Therefore, I must turn my whole energy to saving her." Peirce suspected tuberculosis and knew that living in a house under construction in the winter time was putting Juliette at serious risk, so he arranged for her to travel to the South. She left sometime in February, staying for a time in Brunswick, a resort town on the Atlantic coast of Southern Georgia, and then offshore at the very exclusive and expensive Jeckyl Island Club, where, at the request of Mr. Henry E. Howland, she had been extended privileges for two weeks. From Jeckyl Island, Juliette traveled to the new Hotel Ponce de Leon in St. Augustine where, Peirce wrote to Jem, "she found the greatest benefit" (30 March 89). She telegraphed Peirce from Jacksonville, Florida, on 30 March to say that she was much improved and would like to return, but Peirce tried to discourage her: "You must not think of coming back here so soon. This house is very unwholesome. I have not had a single well day since you left. The spring air would also be the death of you. You cannot come back till after the carpenter work is done. . . . We are rushing the work all we can, but I don't expect it will be ready for you to move into the front part before May 1 & not into the new part for another month at the very least. To move into a new house with the plaster not thoroughly dry would be madness." It must have added to his worry about Juliette to learn that on 29 March his friend and former student, O. H. Mitchell, had died of pneumonia at thirty-seven years of age.
As the days grew warmer Peirce’s own health improved and he became excited at the prospect of farming Quicktown. He purchased two farm horses for harvesting hay, decided to raise a calf that had been born to his Guernsey cow, had five hundred Palmetto asparagus plants set out, and was probably as content as he had been for many years. He missed his young wife and considered renaming Quicktown "Sunbeams" in her honor. When Juliette returned she had not improved and in May Peirce asked for a two-week leave from his Coast Survey duties to take her to New York for medical tests. The diagnosis was tuberculosis, as Peirce had feared. They returned to Milford for the summer and fall knowing that Juliette could not spend the next winter in Milford. That realization was perhaps less worrisome than it would have been had Peirce not recently received fairly substantial payments from the estates of his mother and aunt—$1450 in April alone.
Certainly given the demands of the farm and the renovations to the house, and his preoccupation with Juliette's health, along with the pressure from his continuing responsibilities to the Century Company and the Coast Survey, Peirce had little time for anything else. But occasionally something would happen to turn his thought from its main course. Perhaps this happened most frequently as a result of the great variety of subjects he had to look into for his definitions, but there were other sources of intellectual stimulation and diversion. At the beginning of the year, Kempe's paper on mathematical form had played that role. In March, Wolcott Gibbs had written to Peirce to ask if he had published any results from his color experiments that had been funded fourteen years earlier by the National Academy of Sciences with a grant from its Bache Fund. Gibbs's request seemed to reawaken Peirce’s interest in color studies and for several days beginning 4 April, he recorded results of a new series of color experiments in a notebook labeled "Hue" (1889.12). Peirce traveled to Washington D.C. during the third week of April to present a paper "On Sensations of Color" (1889.14) to the National Academy. He presented a second paper, "On Determinations of Gravity" (1889.15), in which he discussed his work with the invariable reversible pendulums he had designed. The spring issue of the Proceedings of the American Society for Psychical Research carried Gurney's final reply to Peirce (sel. 19) which must have caught his attention, but with Gurney by then deceased, Peirce probably had no thought of any further response. Within a few months, however, he would take up the subject again for The Forum. And in June at Harvard's commencement, Percival Lowell delivered the annual Phi Beta Kappa poem and took the occasion to commemorate Peirce’s father, Benjamin, and Oliver Wendell Holmes. Lowell's Peirce stanza ended: "Though but an echo find itself in verse, The Cosmos answers to the name of Peirce." 36 Charles would surely have heard of this and it could not but have reminded him that he was expected to wear his father's mantle. No doubt he felt the irony that while such grand things were being said about his father, he was, largely by his own doing, living in exile from his father's social world. The promise of a new life may have made things easier for Peirce, but that would not last long.
During the years covered in this volume, the one continuous focus of Peirce’s intellectual energy was his lexicographic work for the Century Dictionary, which in its first edition ran to 7046 quarto pages. He had begun writing definitions as early as 1883 and he continued with varying degrees of concentration from then on, but his most sustained and intensive effort came between 1888 and 1891. Peirce’s contribution to the Century Dictionary was massive. He was responsible for six major subject areas—logic, metaphysics, mathematics, mechanics, astronomy, and weights and measures—but he contributed to many other areas including color terms, general philosophy, geodesy, psychology, and education (in particular, the words related to universities). Altogether he probably contributed or approved over 15,000 definitions, with many of them taking many hours of thought and research. 37
From the beginning, Peirce’s lexicographic work had a decided impact on his intellectual development. At Johns Hopkins, where Peirce began working for the Century Company, he developed a course in philosophical terminology structured around his dictionary work. His desire to express usefully but as fully and accurately as possible the meanings of words such as "classification," "color," "continuity," "formal," "law," "logic," "nominalism," "predicate," "probability," "real," "relation," "science," "sign," "theorem," "truth," and "university," among many others, often led to significant developments in his ideas or in the direction of his thought. Max Fisch believed it was Peirce’s return to the Greek philosophers for his dictionary work that led him to his evolutionary metaphysics, and it is likely that some of the mathematical selections in the present volume were stimulated by his lexicographic work (e.g. sel. 40). Certainly Peirce’s increasing interest in classification, in the history of language, in the ethics of terminology, and in such matters as spelling reform, grew directly out of his work for the Century Dictionary.
It is unclear in what order Peirce took up his dictionary work, but he appears to have begun in 1883 by working his way through the Imperial Dictionary (the basis for the Century ) letter by letter, pronouncing judgment on the Imperial's treatment of his words, emending what could be saved and supplying what more was needed—often a great deal. By 1886 he had reached "Words in E" (W5: sel. 57). But Peirce also worked on his definitions by subject areas, beginning in 1883 with definitions for selected mathematical terms, followed in the intervening years by similar efforts for color terms, metrological terms, university terms, and so on. The Century was an etymological dictionary and included carefully chosen quotations to illustrate the history of the use of its words, so during these years Peirce’s intellectual purview was profoundly expansive, covering the wide range of subject areas he was responsible for and the full history of the words from those areas, from their baptisms, if that could be found out, to their most current uses. He was always on the look-out for illustrative quotations to send in to the Century Company's New York office.
Sometime near the beginning of 1888, but perhaps not until the spring, Peirce started to receive galley proofs for his definitions. The Century began appearing in print the following year in bound fascicles of about three hundred pages. This process of working over the galleys incrementally, while publication was proceeding with earlier fascicles, would continue until the final fascicle, the twenty-fourth, was published early in 1891. By the end of November 1888, Peirce was through the first galley proofs for the F's and on 7 January he wrote Jem that he had received a second galley for "function." By the spring of 1890, the end of the period covered in this volume, about half of the Century was in print. Because of this piecemeal production process, from 1888 to 1891 Peirce had to revisit all of the definitions he had written during the previous five years and compose for each fascicle, as a continuing matter of priority, any definitions he had put off along the way. There is nothing that occupied Peirce more completely during these years than his dictionary work, neither his work for the Coast Survey nor his philosophical system building. It was likely this concentration that led him to set aside his "A Guess at the Riddle" manuscript, just as he seemed to have the book well in hand.
It did not take long after the first of the twenty-four slim volumes of the Century Dictionary appeared in print for reviews to follow. One lone voice of dissent was heard—the voice of Simon Newcomb. In a letter to the editor of the Nation, published on 13 June 1889, Newcomb complained of certain Century definitions that were "insufficient, inaccurate, and confused to a degree which is really remarkable." The examples he gave were for "Almagest," "albedo," "eccentric anomaly," "absorption lines," "law of action and reaction," "apochromatic," "alidade," and "achromatic lens," five of which, it turned out, were Peirce’s. Peirce replied in the 27 June issue of the Nation, admitting that his definition of "anomaly," "perhaps the first I wrote in astronomy," was flawed, but defending the rest. Newcomb confessed to great surprise when he found out it was Peirce he had taken to task, but privately, in a letter to William D. Whitney, Editor in Chief for the Century, he wrote: "I may say to you confidentially that several years ago I should have regarded Peirce as the ablest man in the country for such work but I fear he has since deteriorated to an extent which is truly lamentable." 38 A few days earlier, Whitney had written to his brother that he did not understand why Newcomb felt "called upon to strain the truth and misjudge things in order to find fault" with the dictionary. "It seems," he went on, "as if he must have some private grudge to satisfy." 39 But Newcomb's criticism quickly faded out against the countervailing tide of acclaim. Overall Peirce was quite satisfied with the results of his work, even though he would often remark, as he did to Paul Carus on 25 September 1890, "God forbid I should approve of above ª of what I insert."
The second major preoccupation of Peirce in 1889 was the preparation of scientific reports for the Coast Survey. For years he had accumulated gravity data with painstaking effort and at great expense, and beginning about 1887 had been trying to prepare results for publication. He had not published a major report since 1884, and that was a report on gravity determinations made in Pennsylvania in 1879 and 1880 (W5: sel. 1). Since then he had published some smaller reports, mainly on theory (e.g. W5: sels. 42, 43, 51-53) and, of course, his report on pendulum operations at Ft. Conger, but his principal gravity findings since 1880 remained unpublished. Most importantly, with the exception of the Greely report, these included all of the gravity work carried out with the Peirce invariable reversible pendulums. These unpublished results involved ten stations, six running along a north-south line between Montreal and Key West (including Albany, Hoboken, Ft. Monroe, and St. Augustine), three along an east-west line between Ithaca and Madison (including Ann Arbor), and the base station at the Smithsonian in Washington D.C., which provided the constants for all the Peirce pendulum operations.
In addition to reports on gravity work involving the Peirce pendulums, results still had to be worked up for earlier operations with Repsold or Kater pendulums at Hoboken, Cambridge, and Baltimore and for some of Peirce’s early gravity work with less refined pendulums in Massachusetts (at the Hoosac Tunnel, Northampton, and Cambridge). Also, there were at least three volumes of unreduced data from observations made at Paris, Geneva, and Kew during Peirce’s final trip to Europe in 1883. All of these records together, in their raw data form, filled more than one hundred volumes of pendulum transit records and scores of chronograph sheets recording time observations.
Finally, in conjunction with his principal work of determining gravity, Peirce had applied his results to the problem of determining the shape of the earth and had made many studies and investigations of such issues as the flexure of the pendulum staff and the effect of air resistance (involving hydrodynamical theory). For that, too, he needed to prepare reports.
Peirce had begun in earnest reducing data and writing a report on operations with the Peirce pendulums in the fall of 1886, after being relieved of field duty, but his attention had soon turned to the Greely report. Upon settling in Milford, Peirce turned again to the preparation of the report he believed would carry forward the U.S. contribution to geodesy he had initiated with his 1876 "Report on Gravity at Initial Stations" (W4: sel. 13) and his "Determinations of Gravity at Allegheny, Ebensburgh, and York, Pa., in 1879 and 1880" (W5: sel. 1). His plan in June 1887 was to write first a report on what he thought was the best work done with the Peirce pendulums, the results from Ithaca, Madison, Ann Arbor, Key West, and perhaps Fort Monroe, and to give "a full account" of the pendulums, including a discussion of their theory and of the work that had been done at the Smithsonian, the base station, to determine their constants. Then, for a separate report, he planned to prepare the results from Hoboken, Albany, Montreal, and St. Augustine, also done with Peirce pendulums, but not "in the last approved way" (9 June 1887). 40 But by the end of the year, Peirce had decided to organize the work into two series of stations grouped by their approximate location on either the same east-west or north-south meridian. After he finished his reports on work with the Peirce pendulums, he planned to clean up the remaining backlog.
Peirce went to work on the report for the east-west series of stations and wrote to Thorn on 28 June 1887 that it was "shaping up" and that he would soon have a draft ready, but he added: "it is a larger job than I fully realized." Two months later Peirce still had not finished his draft and he was forced to admit that he had run into a serious difficulty: he had found an error in the mathematical theory used to calculate the effects of the viscosity of air on the period of the pendulum. "This is one of the most difficult mathematical problems conceivable," Peirce wrote to Thorn (29 Aug. 1887), but he expected that his work would lead to an improvement in Stokes' hydrodynamical theory which would justify the delay; by the end of September Peirce decided that he should put off further treatment of hydrodynamics for a separate memoir. The final illness and death of Peirce’s mother kept him in Cambridge for most of the month of October 1887, but by the end of November he wrote Thorn that his "long report" was almost ready, "requiring only final touches." Two months later, on 30 January 1888, Peirce sent in what he had ready "for the sake of suggestions of which I may avail myself in making the copy of it." He acknowledged that a lot of work, mostly clerical, remained unfinished and asked if he could have some assistance. Thorn declined and returned the draft unreviewed to be finished and copied.
Weeks passed by and Thorn's displeasure increased. On 30 March Peirce felt the need to explain the continuing delay. Pendulum work, he pointed out, is much more complicated than other geodetic work such as triangulation, longitude work, and leveling, because there are so many more sources of error that have to be studied and corrected for. "If these difficulties are only slightly increased, there results an enormous increase, first in the precautions which have to be taken in the field, and second in the puzzle of interpreting the observations." Defects in the construction of the Peirce pendulums, which Peirce attributed to poor American craftsmanship, made it all the more difficult to reach useful results, and the problem of hydrodynamics, now to be treated separately, had taken considerable time. "Now anybody who has ever done such a Work in such a way,—ask such men as Langley or Newcomb,—will tell you that it is impossible to make any reliable estimate of how much time it will take." Peirce’s emotions were at a high pitch and he could not resist an allusion to Colonna's obstructionism: "In addition to this, I was subjected to false accusations of the most disgraceful kind, and the newspapers were filled with unbounded lies about me readily traceable to important personages. All of these things, and others which I omit to mention, distracted the equanimity of my mind considerably." In the margin of Peirce’s letter, Colonna added the sarcastic remark: "What about other people's distractions of mind[?] Also what distracted his mind at all except the last 3 stations?" This was a clear reference to Peirce’s relations with Juliette, and the fact that she had accompanied Peirce on many of his field assignments. Even though Peirce would not have seen Colonna's remark, Thorn and others in the Washington office would have; it indicates that rumors of scandal had infected Peirce’s Coast Survey relations with the poison that had driven him from Johns Hopkins and had virtually sent him into exile. Peirce felt compelled to respond to the irritation and displeasure Thorn had been exhibiting:
The tone of your letters would seem to betray the opinion that I am myself completely insensible to the disparity between the time I estimated for the work and the time it has occupied. But can you suppose that I do not look upon the labor of my life seriously? Or that anything that you or the Hon. Secretary could say or do about it could possibly be as grievous to me as the want of my own self-commendation? When I agreed to do this work by myself my intention was to hire a computer; for I do not believe that anybody in the world could do such work advantageously without aid. The papers amount to at least a hundredweight and the mere picking out of such as are wanted in one day will all together often occupy hours.
Peirce took time in July to work on the method for calculating the figure of the earth from gravity determinations and on 10 August submitted his results for publication. For the rest of the year, again without an assistant, Peirce continued to work on reductions of data and on flexure and time calculations. On 31 December 1888, following a recommendation from C. A. Schott, he wrote to Thorn suggesting that both series of stations be included in one comprehensive report: "The amount of additional computation required is considerable, although not so great by any means as if the constants & behaviour of the instruments had not been studied." Peirce added, with some obvious bitterness: "The labour of writing the report,—of composing it, writing it, copying, verifying copies,—which is in part mechanical and in part requires all the ability I can bring to the task,—but in every part the utmost care and consideration, has mostly to be done over."
You will remember that about a year ago, I sent you my report in a substantially complete state (though then only embracing 4 stations) with the request that it be submitted to such critical examination as might be practicable and the result communicated to me for my aid in revision. The request was refused; and your letter embodying the refusal, conveyed to me the conviction that any flaws however trifling which might be detected would be husbanded to form material for an attack after the report was printed. Under these circumstances, my caution about parting my MS. out of my hands is naturally increased. . . . I am unable to say more definitely at what time my report will be ready, than that it will be during next spring.
On 11 January 1889, Peirce reassured Thorn that "the full report on the meridional line from Montreal to Key West inclusive & from Albany to Madison inclusive will be completed during the Spring," but Thorn, at Colonna's instigation, had lost faith in Peirce and decided that it was time to see exactly where things stood. He ordered Peirce to package up all of his work on the report and ship it to Washington for examination. Peirce complied, and two days later had packed and shipped twenty large books of reduced data and 2037 carefully inventoried and numbered manuscript pages and draft materials (see p. 636). Peirce could not let pass unaddressed the distrust that Thorn's order so clearly revealed. He told Thorn that he was glad to send all of his working documents because, for one thing, it would rebut the insinuation that the draft report he had sent the previous year had represented little effort on his part. But Thorn would also see that a great deal had been accomplished since then "and that the principal cause of the delay in completing the work has been the great amount of time spent upon the general method of pendulum observations and reductions,—which lay directly in my way." Peirce estimated that he needed at least three more months to complete the report and he asked again if he could submit it in draft to be looked at by specialists before making his official submission. Taking Thorn to task for a previous refusal, he added presciently:
You say your object was to prevent my shifting the blame for the report to other shoulders. Now, for my part, I really do not think the report will sink below the zero of merit; but anyway, you overlook the fact that I never asked for binding directions but only for suggestions which I might be free to adopt or not. My main, not to say my only, motive was that I had reversed the usual order of presentation in a scientific memoir by stating the conclusions before the premises; and I wished to know how this would strike another mind competent to judge of it. (30 January 1889)
Peirce’s relations with Thorn were at a very low point, yet, having unburdened himself, Peirce put his rancor aside and tried to resume normal relations. He wrote to Thorn on 4 February to say that, while the Peirce pendulum records were in Washington, he had gone to work on the Kater pendulum records from his Hoboken observations. He asked if he might go into the field again in the South—without mentioning that he was about to send Juliette to Southern Georgia for her health. Thorn declined. A few days later, Thorn returned all of Peirce’s records "precisely as received from you—with the exception of Ms. report of pendulum work, which is in your handwriting and is retained for safe keeping in the archives here . . ." (13 Feb. 1889). 41 Peirce resumed his work on the long report and by the end of April had finished the reductions for the Montreal and Albany stations.
Whether Peirce knew on 30 January, when he wrote his spirited letter, that Thorn was about to resign is uncertain, but by mid-February it was common knowledge that Thorn would tender his resignation in March to be effective when a new superintendent was appointed. Peirce had hoped for this for a long time; he thought that a new superintendent, if a scientist were chosen and not another lawyer, would want him back playing a more active role in Survey operations. This may have had something to do with Peirce’s request to go back into the field and was surely on his mind in May when he wrote to Thorn about a plan he had conceived "by which pendulum stations may be occupied perhaps at the rate of one a day, with good result, and not at an extravagant expense" (28 May 1889). He asked Thorn again to send him back into the field to institute his new plan as soon as he finished his pendulum report, which he said would be forwarded soon. Thorn replied on 14 June with a reminder of Peirce’s "repeated promises during the past winter" that he would soon forward the report, "and now the Spring has passed." He advised Peirce "that no other enterprise or scheme be permitted to interfere with the prompt completion of that long delayed report, upon receipt of which your plan of daily pendulum stations will be in order for submission and consideration."
On 10 July 1889, Thorn was succeeded by Thomas Corwin Mendenhall as Superintendent of the Coast Survey. Mendenhall, who had been a student of Simon Newcomb, 42 was a physicist who had taught at universities in Ohio and Tokyo before joining the U.S. signal-service in 1884. In 1886 he had assumed the presidency of Rose Polytechnic Institute in Indiana, and it was from there that he had been called to the superintendency of the Coast Survey. Mendenhall seemed well suited to lead the Survey and Peirce was delighted with his appointment. Peirce’s telegram of congratulations, sent to Indiana, was the first that Mendenhall received and he replied that it had given him great satisfaction. Peirce sent his first monthly report to Mendenhall on 31 July and took the opportunity to give a very detailed account of his pendulum work for the many years he had been in charge of gravity research. He also described at length his relations with Thorn and his general unhappiness with the direction the Survey had taken over the last half-decade.
When Mr. Thorn came in, certain charges were made against me. Later, all these were retracted with the exception of one, which was a very vague one to the effect that I had not been under proper control and discipline. Now, if I were to be informed what the questions about gravitation were, and what the facts of the case on which the solution of those questions must depend, all the discipline in the world could hardly prevent my having my way, for the simple reason that "my way" is simply what I deem reasonable, and as my ideas on this subject are clearer than other persons', they must prevail with those very persons themselves. Accordingly, to prevent my having "my way," I have of late years been kept as far as possible ignorant of pendulum matters. I trust you will reverse this policy, and restore me to the charge of investigations into gravitation.
As to the report Thorn had been waiting for so impatiently, Peirce wrote that it was in a typist's hands. He had been working on a new arrangement for the report and now intended to submit it in two parts with the first one covering the work done at the Smithsonian, Ann Arbor, Madison, Cornell, and Key West. There were yet further delays, but finally on 20 November Peirce was able to write the agreeable letter that would accompany his long-delayed report (sel. 36). Although it did not include the Key West results, his submission included all of the theory, history, and discussion of constants needed for the complete report on the Peirce pendulum operations. As it was, the report ran to one hundred and forty oversize typescript pages. Peirce promised that a report on Montreal, Albany, Hoboken, Fort Monroe, St. Augustine, and Key West would soon follow, and could be published later as the concluding part of the comprehensive report.
Although Peirce’s report included all of the basic component sections present in his 1879 report (W4: sel. 13), it strikingly reversed their arrangement. Peirce also used radically different methods, the most obvious one being the introduction of "logarithmic seconds" as a unit of measurement. He also made a different application of the "resistential formula" which occurs in both reports as the basis for calculating the effect of air resistance. It is in this determination of corrections for the "second atmospheric effect" that Peirce hoped to improve on the classical theory of G. G. Stokes. As the annotations in this volume help to make out, though all of the necessary components are present, they do not all fit together entirely smoothly, and the report is marred by computational errors. This is not surprising, given the massive quantity of calculations that Peirce had to make in order to achieve his results; it is clear, however, that the report needed a thorough overhaul before it could be published.
Perhaps had Thorn still been superintendent, Peirce’s report would have followed a standard course of technical examination, proofreading, and publication, but Mendenhall was new, and he had been encouraged not to fully trust Peirce’s work, so he chose to have Peirce’s report examined by specialists for "form, matter, meaning and suitability for publication." One of the three people he asked to examine the report was his own mentor, Simon Newcomb. On 28 April 1890, only four days after Peirce’s long memoir had been mailed to him, Newcomb wrote to Mendenhall that it appeared to be "a careful and conscientious piece of work," but that its form was wrong:
A remarkable feature of the presentation is the inversion of the logical order throughout the whole paper. The system of the author seems to be to give first concluded results, then the method by which these results were obtained, then the formulae and principles on which these methods rest, then the derivation of these formulae, then the data on which the derivation rests, and so on until the original observations are reached. The human mind cannot follow a course of reasoning in this way, and the first thing to be done with the paper is to reconstruct it in logical order.
Newcomb also objected to Peirce’s reliance on logarithmic seconds, which he believed accomplished nothing except to confuse the reader. "On the whole the paper does not seem to me one which would prove useful scientifically or would redound to the credit of the Survey if published in its present form." Ultimately, Mendenhall would decline to publish Peirce’s laboriously ground-out report and would justify his decision with words that echoed Newcomb. On 21 September the following year, having decided that Peirce’s report as submitted was not publishable, and still waiting for the report for the north-south stations, Mendenhall would inform Peirce that his services would be discontinued at the end of 1891. That would bring to an end Peirce’s thirty-one years of federal service and, without a pension, Peirce would have no regular income. As for Peirce’s 1889 report, it would be bundled up in brown wrapping and sent to the archives where it would disappear, mislaid, for more than seventy-five years.
At the end of the period covered by the writings in this volume, Peirce’s report was still under review, and nearly a year and a half would pass before Mendenhall would write the letter informing Peirce that his services were no longer desired. But given how much time Peirce spent preparing the 1889 report, and how crucial a role it played in determining his fate, it seems appropriate to consider a little further some of the circumstances pertaining to the report's composition and quality. A number of delaying factors have already been noted, including Peirce’s commitment to other writings and projects, his attending to family matters, and also his discouragement, perhaps even depression, over his treatment by the Washington office. But Victor Lenzen, in the best study to date of this report, 43 emphasized two additional factors that must be taken into account.
Since 1883, Peirce had waited in vain for new pendulums from Paris, with which he hoped to improve upon the results obtained with the set of Peirce pendulums. The latter had been manufactured in the U.S. in 1881, and data obtained from their use required many corrections that could be avoided with better constructed pendulums. While in Paris in 1883, Peirce had arranged with P. F. Gautier, instrument maker for the French Bureau of Longitude, for new pendulums to be constructed according to his own improved design, and it was a constant source of frustration that he had not been allowed to stay in France until the pendulums were finished. He kept hoping until his final days with the Survey that they would be sent for.
A related but more general reason for Peirce’s slow progress was his insistence, for his own reputation and that of the Survey, that his pendulum work met the highest standards of scientific performance. He could not accept the view that had become entrenched in all levels of U.S. Government that only fast practical results were wanted. Peirce was working to advance science, and it was thanks to the precision of his research that he had earned the respect of his peers. He could not surrender to what he believed to be anti-science.
Another important factor in that contributed to the demise of Peirce’s report was Mendenhall's disagreement on how gravity results should be represented. Peirce was adamant in his view that gravity is best understood as an acceleration, not a force, 44 and that relative determinations of gravity—where gravity at a location is measured relative to gravity at another location—provide greater accuracy than absolute determinations and are all that is needed for determining the figure of the earth. In his report on gravity at Fort Conger (sel. 30), Peirce had introduced a new relative measure that he called "logarithmic seconds." These new units, reintroduced in the 1889 report (sel. 36, pp. 289-90), were meant to facilitate the calculation and use of gravity results. Lenzen explains that when gravity is expressed in logarithmic seconds, "a difference of values of gravity at two stations in log. secs. is numerically equal to the difference in the corresponding numbers of oscillations per day at the stations of a pendulum that beats seconds at the mean equatorial station." 45 Mendenhall, for his part, was equally adamant that gravity should always be expressed in units of force called "dynes" and, besides, he thought that Peirce’s logarithmic seconds were obscure and confusing. He was not moved by Peirce’s defense that they were not obscure to mathematical geodesists, "men who have to deal with the most intricate parts of the calculus," and that they had the very useful effect of "making all the operations of reduction and comparison additions & subtractions in place of multiplications and divisions" (22 July 1890). Mendenhall told Peirce that of course it was his own business how he wanted to restrict the meaning of "g" for his personal use, but that "when acting for the public . . . one must be guided by the general consensus of opinion of those generally admitted to be the highest authorities; personal preferences and especially any weakness towards `eccentricity' must often give way" (24 July 1890). Mendenhall was unwilling to recognize that at that time there was no one in the United States who was a higher authority in these matters than Peirce.
A more important disagreement between Peirce and Mendenhall concerned the method for conducting gravity operations and the precision to be aimed for. Mendenhall had become persuaded that it was acceptable to give up absolute determinations altogether and, in general, to sacrifice precision for economy as long as results were satisfactory for ordinary practical purposes. Accordingly, Mendenhall, following the lead of Robert von Sterneck of Austria-Hungary, had adopted a new style short "half-seconds" invariable pendulum that could be carried from station to station and put into operation at a fraction of the cost associated with Peirce’s use of the yard and meter pendulums, especially their use in the complex operations required to determine absolute values. 46 In his first gravity report, published in 1892, Mendenhall explained that the Coast Survey would no longer follow the traditional European-style gravity studies that Peirce had instituted in the U.S. because they were too expensive, cumbersome, slow, and inefficient. The half-second pendulum, by contrast, solved all of these difficulties: "One of the principal advantages of this apparatus is the ease with which it may be used, and the few and inexpensive preparations necessary for its installation." 47
In June 1894, two and a half years after Peirce’s forced resignation, Mendenhall testified before the Congressional Committee on Naval Affairs where he was questioned about Peirce. 48 He told the Committee that much of Peirce’s work "was of the highest character, and it has received praise from the European geodesists and others, physicists, etc., but it lacked the practical quality which I believed to be essential." He explained that after the successful introduction of his half-second pendulums, he "became convinced that Professor Peirce’s services to the Survey were no longer necessary." Mendenhall added that the results Peirce had been working on in his final years had not been published because Newcomb and other experts had judged that they were "not valuable."
Was that a fair assessment of the results Peirce worked so hard to obtain during his last years at the Survey? It is difficult to evaluate scientific work that never became part of the public record, but Lenzen concluded that Peirce’s unpublished monograph was much more important than Mendenhall supposed. Some of Peirce’s accomplishments, according to Lenzen, are the following: 49 1. Peirce’s calculation of "provisional maximum values of the departure of the geoid from the mean spheroid" (pp. 289ff.) is one of the earliest applications, if not the first, of Stokes's theory of the form of the geoid. 2. Several of the corrections used in the report were original with Peirce. These include the correction for flexure of the pendulum support (pp. 295-99), which Peirce had introduced in his 1876 "Report on Gravity at Initial Stations" (W4:131-33); the correction for the unequal expansion of the upper and lower parts of the pendulum, introduced by Peirce in 1885 (W5: sel. 53) but first applied in the 1889 report (p. 341); the correction for the inclination of the knife-edge (pp. 340-41); and the correction for the second atmospheric effect. 3. Peirce’s calculation of the absolute value of gravity for the Smithsonian station, appropriately converted, appears to match a result obtained seventeen years later by the Geodetic Institute at Potsdam, which became the reference value throughout the world. 50
In considering the importance of the 1889 paper, Lenzen emphasized the significance of Peirce’s "second atmospheric effect," the effect of the viscosity of air on the motion of a pendulum. Peirce had introduced this correction in his report for 1876 (W4:104-106) but only as an a posteriori correction. In the 1889 paper he applied and compared both a priori and a posteriori corrections, for he had designed the Peirce pendulums to facilitate just such a comparison for the viscosity correction. The theory Peirce applied was that of G. G. Stokes, but the formula Peirce used for his calculations took account of more factors than did Stokes's formula. Lenzen concluded that it was unfortunate that Peirce’s "highly original discussion of the second atmospheric effect" had not been published, for it would certainly have been of interest to "Professor Stokes, Lucasian Professor of Mathematics, and in charge of the British Gravity Survey." Lenzen closed his study with the following assessment: "In the light of a review that I have made of the development of pendulums for the determination of gravity, it is my firm judgment that the experimental and theoretical work represented in Peirce’s Report on Gravity at the Smithsonian, Ann Arbor, Madison, and Cornell was the best work of its kind in the nineteenth century." 51 However, as was pointed out above, Peirce’s report was far from finished, and had it been published without improvements, his innovations might well have gone unheeded.
Life for the Peirces in their new house, during its renovation in the summer of 1889 could not have been idyllic. Overseeing construction and running the estate would have been pressure enough, but Peirce was expected to give full days of attention to his work for the Coast Survey, and somehow find time to write his definitions. Besides, many other lines of thought were constantly working themselves out under his pen. In August, Peirce published in the Nation a review of St. George Stock's Deductive Logic (sel. 35). It was Peirce’s first review for the Nation since reviewing Abbot's Scientific Theism (W5: sel. 46) in 1886. Peirce’s review of Stock was the kind of review an author dreads; the best Peirce could say was that "it would be impossible for a man who has been studying and teaching logic at Oxford for seventeen years to write a thoroughly bad book on the subject," but he added immediately that any teacher who decided to use Stock instead of Bain "would be doing his pupils an injury." Peirce was not one to mince words. He declared that "the best expositions of the subject" force students step by step to see the close connection between "formal rules and the trains of thought which actually go on in their own mind" and that every logic text should have at least a brief treatment of symbolic logic. Stock's book failed on both counts. Peirce announced that "there is no subject in which there is more urgent need of a new book," probably knowing he would soon resume his own effort to fill that need (see W5, sels. 54-56). By the end of 1890, he was working to transform his correspondence course lessons into a text book entitled "Light of Logic." The fragment that the present editors have entitled "Reasoning" (sel. 37) probably dates from early 1890 and may have been written with such a book in mind.
By the end of September the first phase of construction at Quicktown was complete. Peirce wrote to Jem with some satisfaction that "our house" is "very comfortable, very pretty" and "not in the least in the Queen Anne nor any other style. It is our own original style" (30 September 1889). He continued with a description of his estate and plans for its development and added: "I am confident that we shall eventually make money from this place." But this was to remain the elusive silver lining. Peirce’s enthusiasm for Quicktown, his dream of a comfortable, even elegant, country life with Juliette, had already begun to fade. In part this was due to the combined demands of managing the renovations, running the farm, and his professional work, but that was not all. He continued his letter to Jem: "But now I must turn to quite another side of the canvass." The other side was "dear Juliette's health." Peirce told Jem that her diseased lungs were even worse than they had been the previous year when she had been warned not to spend her winters in the North. Clearly, she would have to winter elsewhere again this year. To make matters worse, Juliette had become very depressed, a condition Peirce might have been prone to as well. 52 On 11 July in an outburst of anger and frustration, Peirce struck a domestic helper, Marie Blanc, and a few days later was charged with assault. Joseph Brent speculates that Peirce may have lost his temper while attempting to upbraid Miss Blanc for not following Juliette's orders. 53 Such domestic tension could only have added weight to the pall that was descending over Quicktown. The case was not resolved until October when Peirce pled guilty to one count of assault and was fined twenty-five dollars plus court costs. Everything taken into account, life for the Peirces in the summer and fall of 1889 had taken a decided turn for the worse and tensions were mounting. But Charles and Juliette were resilient and still usually hopeful. In November they added significantly to their land holdings by purchasing an additional 1200 acres of woodland. Apparently Peirce was growing used to his new life. He continued his 30 September letter to Jem: "This living in the country is highly conducive to reading long works in many volumes. I have not a rage for reading; indeed I think an impulse to study and an impulse to read are rather antagonistic; but I get through a good many books here. I find nothing wears better than Sainte Beuve."
Had Peirce and Juliette been content with modest country living, with an excellent library to fill their idle hours and with only infrequent trips back to New York for a fashionable dinner or an evening at the theater, they might have managed to avoid the terrible poverty that lay ahead. But they seemed determined to amass a great estate—adding yet another five hundred acres the following year—and modest living seemed to be out of the question. When it became necessary to deal with Juliette's winter convalescence, much of Peirce’s inheritance had been used up—the greater part that he had already received. Yet cost does not appear to have been a factor. Peirce explained to Jem that because of Juliette's depression, he thought it "absolutely indispensable that she should be where she finds amusement" (30 September 89), and he thought that Sicily might be the place for her. As it happened, Jem had been in Europe for nearly three months and would be there for several more. Relations with Jem had improved since Aunt Lizzie's death, and Peirce was relieved to have him there to watch out for Juliette.
On 21 November 1889, one day after Peirce had finally submitted his long overdue gravity report, a notice appeared in the Milford Dispatch announcing that Juliette would soon make a journey abroad for the winter in quest of health. Six days later Peirce watched Juliette and their dog, Bliss, board the SS Entella in the New York harbor, bound for Naples. Two days later Peirce wrote to Juliette: "What a terrible afternoon & night it was after you sailed! How did you get through? I was terribly anxious." He told her he had seen the Pinchots, who lived in New York City except for the summers, and they had invited him to dinner, but he had declined because he did not have dress clothes with him. He had taken his Thanksgiving dinner at the Century Club with John La Farge and Clarence King. "I expect to get away this afternoon, but may not. They haven't been very polite to me at the Lenox, & are evidently trying to get rid of me. I could not stay there with the least self-respect. I don't pay enough. . . . Dear little girl! I do nothing but think of you, & can't help talking too much about you. Good bye! Write from Gibraltar."
Indeed, Peirce could not stop thinking about Juliette or his money woes. He wrote to his friend Annibale Ferrero, an Italian mathematician and geodesist who lived in Florence, to ask if there was not some position for him in Europe. He indicated that he would be prepared to leave the U.S. at once—perhaps hoping secretly to find a way to join Juliette while she convalesced. He had inquired of G. S. Hall a few weeks earlier about the possibility of a position at Clark University, so apparently he had begun shedding his illusions about Quicktown. Ferrero wrote back on 25 November urging Peirce to be patient. He was sure there could be something for Peirce with the International Geodetic Association, something appropriate to a scientist of his international reputation, but that sort of arrangement could not be hurried. With Juliette away, Peirce decided to spend as much time as he could in New York to see if he could find a way to turn his writing into cash. By now he must have understood that the correspondence course would never bring him much income and that if the farm were ever to make a profit, it would not be soon. He may have been feeling a little more secure about his Coast Survey salary, having just turned in the long report, but he had promised, quite unrealistically, that the second part would be finished promptly and he knew that before long he would be asked to turn it in. But even if he could keep his income from the Survey, that would not be enough—at least not until the farm could generate a substantial annual income. The immediate problem was to keep Quicktown operating and to provide for Juliette in Europe. Peirce had used up all of his reserves, and he was not sure how he would earn the money for the monthly disbursements he had promised Juliette.
Peirce wrote to Juliette again on the 6th of December. At the top of his stationary in place of "Quicktown" he inscribed "Sunbeams," a name he sometimes called Juliette as an endearment. He was feeling lonely and greatly missed her. Beside the word "Sunbeams" Peirce made the impression of a kiss. André De Tienne has speculated that it may be from an anagram play on "baiser," the French word for kiss, that Peirce first got the idea to rename his estate "Arisbe" as he soon would do. 54 He wrote to Juliette about finances. He told her that he had returned to the farm and had been working twelve and thirteen hour days. In New York, Pinchot had encouraged him about the prospects for an arithmetic book he had started, but Peirce thought it doubtful that such a book could bring in more than $1000 a year, and other books he thought he could produce would not bring in more than half that. "Thus, you see if I write 4 with my own hand, the most I can expect is $3000 a year from them; and from all I can write myself or ever get written $5000 a year will be the most. We are spending that now." On a more positive note, he told Juliette that he had learned that tuberculosis was not incurable, even though some lung damage might be permanent. Finding this out had been such a relief to him.
Peirce was running out of options. He tried to borrow from his friend George Butler. On 8 December, Butler wrote that he was "awfully sorry" but that he simply had nothing to loan: "I am probably harder up than you are." Peirce did manage to raise a little money to ease the tension of the moment, but nothing would be more destructive of his relationship with Juliette or of his life overall than his constant and never diminishing, sometimes extreme, need of money. The problem would become almost intolerable in another year, after the loss of his income from the Coast Survey, but the expenses of Juliette's trip abroad made the first half of 1890 almost as difficult. The day before Christmas, Peirce sent Juliette a check for six hundred and fifteen francs, apologizing for the delay and warning her that he might have some difficulty with "the next remittance." Peirce knew that Juliette's steamer had reached Gibraltar on the 16th, but did not know that she had reached Naples when he wrote to her on the 24th: "I have had no letter from you yet. . . . I shall pass Christmas with the old bachelors of the club."
Peirce spent New Year's eve with George Butler and his wife at their country home in the Hudson Valley north of New York City. He had by then received a letter from Juliette, from Gibraltar, and was greatly distressed at how ill Juliette told him she was. He wrote back on New Year's day expressing his concern: "I never would live without the sunbeam of my soul!" But Jem's letters to Peirce suggest that Juliette's stay in Europe came much closer to being the pleasant amusing time Peirce had wanted for her than she was ever willing to admit. On 23 January 1890 Jem wrote from Rome: "Your cablegram did not reach me till the 16th. . . . I telegraphed & wrote to the hotelkeeper at Palermo, & learned that Juliette had already left for Cairo. She is sure not to have been seriously ill, & to have been well lodged & cared for." Jem's opinion is confirmed by an extant medical report from a Cairo physician who examined Juliette on the 24th and found nothing seriously wrong with her. Juliette stayed in Cairo until the end of March. Jem wrote on 5 April that he had seen Juliette several times recently and that he wanted to send his impressions about her state of health. "I cannot help thinking that her winter has been of substantial benefit to her. She speaks of the serious attacks which she still has, & seems to regard herself as doomed. But whenever I saw her, she looked & appeared strong & vigorous, & has evidently enjoyed much in her Cairene life and is familiar with Cairo through frequent visits to its streets & bazaars. . . . I have a strong faith that you will find that she has gained ground since she came abroad." Later Jem would write that he did not believe Juliette was as ill as she imagined but that "She is easily excited & depressed" (13 June 1890). After Cairo, Juliette stayed in Alexandria for two or three weeks and then traveled back to Naples where, according to Jem, she stayed "at the Grand Hotel, a delightful house," waiting for a steamer to New York. There is some obscurity about Juliette's final days in Italy and when she finally sailed for New York, but it seems unlikely that she arrived back before early June.
Juliette had been away for half a year. During that time, Peirce periodically returned to Quicktown to tend to the estate and probably to spend long hours on his definitions, but he spent the greater part of these months in New York where he had friends and where there was more opportunity to make money. On the first of February, Ernst Schröder wrote to Peirce, resuming a correspondence that had lapsed for five years. Schröder told Peirce that the first volume of his Vorlesungen über die Algebra der Logik (exakte Logik) would soon be published and that he had asked his publisher to forward a copy to Peirce. He was concerned that Peirce might have broken off their correspondence out of anger for "some unknown reason." Their ensuing exchange of letters, until Schröder's death in 1902, was a great stimulus to Peirce, especially concerning the logic of relations. On 5 March, Peirce received a letter of self-introduction from Ventura Reyes y Prósper, who also corresponded with Schröder.
Such communications, and meetings with scholarly friends for dinners or at the Century Club, were important intellectual anchors for Peirce during a difficult time. Juliette's absence caused Peirce much distress. At first he just missed her and was worried about her health, but the hardship he endured trying to provide the money she needed led to anxiety and a growing sense of failure. Gradually, with so few letters from her and with those he did receive expressing disaffection and disapproval, his frustration turned to disillusion and sometimes bitterness. Peirce wrote on 23 January, after she had been away for two months: "I have only had two letters. . . . I hear nothing, nothing. Good God, I shall go crazy if I don't hear soon. This is terrible." Three months later, feeling that he had done his best for her but having received not the slightest indication of any appreciation from her, Peirce wrote: "Your letters to me are so full of hate and rage, that I know not how to write to you. What my difficulties have been you do not know." 55 Using the third person, Peirce went on to describe the changes in Juliette's character that he had observed, starting with when they had met.
She was a very true and noble heart, that nothing ever could corrupt. And then I knew her in Washington when she showed capacities which surprized me. Then there was a dreadful period when everything in life was terribly terribly embittered. I wish now I had been drowned before I had to pass through such things. Very gradually, the curse seemed to pass away, & there was a time in Milford when there seemed to be much happiness, shaded by some doubts only. All this time, I was getting to know and to adore this dear lady more and more and to love her more deeply. In the future I don't know how it will be. The present is dreadful.
The letter from Juliette that had agitated Peirce so much is no longer extant, but it is evident that Juliette had made an urgent and probably indignant plea for more money, perhaps claiming that she could not return without it. She must have threatened to sell a watch Peirce had given her for he pleaded with her not to do it and promised to send more money "no matter what happens, very soon." He tried to borrow from friends and acquaintances but apparently without success. He urged Pinchot to hire him to tutor his children at fifteen dollars a week, and probably asked for an advance, but on 5 May Pinchot replied that he could not immediately make up his mind. On 14 May, Peirce wrote to C. R. Miller of the New York Times, with whom he had just concluded a successful newspaper debate on Spencer, proposing a series of fifty articles on evolution, but Miller did not think it could sustain the interest of his readers. As late as the first week in June, Peirce sought a consulting assignment with the Astor Library. By this time, however, Juliette must have already been on a steamer for New York, if she had not already arrived. The record does not indicate how she managed to settle her final accounts in Europe.
It is difficult to know whether Juliette ever understood or even cared about how Peirce had managed to support her European convalescence, or whether Peirce became a changed man as a result. The scant evidence suggests that her anger over what he had not provided outweighed any appreciation for what he had managed to send. The fact is, Peirce had managed to raise money from his writing, and his urgent need for cash had disposed him to try writing as a tool to make money rather than for the straightforward exchange of ideas. Of course Peirce’s stock in trade was his ideas, but he had been more willing than ever to turn them, if he could, to commercial ends. How successful he was still remains to be discovered. Extensive searches of New York newspapers and of contemporary magazines remain to be made with the purpose of digging up anonymous reports or hack writings that might have come from his pen (or typewriter). More may be discovered, but we will probably never know how much he managed to sell during that difficult time.
Sometime early in 1890, Peirce and Wendell Phillips Garrison, editor of the Nation, reached an understanding that significantly increased the number of books sent to Peirce for review. Peirce had occasionally reviewed books for the Nation since 1869, but he had never reviewed more than three in a single year, and his August 1889 review of Stock's Logic had been his first Nation review in three and a half years. Peirce published ten reviews during 1890, and would publish even more in each of the next five years. Only two of Peirce’s 1890 Nation reviews appeared during the period covered in this volume. The first was the review of Noel's Science of Metrology (sel. 43). Noel was an Englishman who was opposed to the metric system of measurement but who believed that the English system should be reformed. Noel proposed changing the ratios of inches to feet, pounds to gallons, and so forth. Although Peirce saw some merit in Noel's proposal, he suggested that to challenge the metric system was "like challenging the rising tide" and that the only thing more futile would be to try to change the length of the inch." The second Nation review was a review of F. Howard Collins's Epitome of the Synthetic Philosophy (sel. 46). This was a very brief notice praising Collins' "second-hand synopsis" for reducing Spencer's "heart-breakingly tedious" five thousand pages to a mere five hundred, but lamenting that Collins had gone over fifty.
If Peirce’s increasing number of reviews for the Nation, many of them also appearing in the New York Post, was in fact an outcome of his overwrought effort to raise money during Juliette's European convalescence, then it should be regarded as his most striking success. For he would produce nearly three hundred more reviews for the Nation and the income supplement from those reviews would be crucial for his and Juliette's survival—and the loss of that income in 1906, after Garrison's retirement, would be a serious blow. 56 But Peirce’s most notable achievement in raising funds while Juliette was away was his success, working with New York Times' editor C. R. Miller, in organizing a debate about the soundness of Herbert Spencer's philosophy that ran for six consecutive Sundays, from 23 March to 27 April. Altogether, the debate consisted of twenty-nine articles and notes. At Miller's urging, Peirce made a great effort to recruit respondents for this debate. One of his prospects, William James, replied on 16 March that nothing would please him more "than to help stone Uncle Spencer, for of all extant quacks he's the worst—yet not exactly a quack either for he feels honest, and never would know that a critic had the better of him." But James begged off because he was so pressed to finish Principles of Psychology. Peirce had sent James copies of his opening article for the Times and probably also his Nation review of Collins, and James wrote that the columns were clever but "possibly a bit too interrogative and transcendentally suggestive to captivate the vulgar." Not having what it takes to "captivate the vulgar" was James's usual criticism of Peirce’s writing. He closed by asking when Peirce’s own "radical evolutionary speculations" would see the light.
A 17 March letter from Miller to Peirce serves to illustrate the nature of their collaboration and how the Spencer series was organized.
I wanted to hold the Spencer article until I could be assured of something in reply to or in support of it for the following Sunday. Prof. Marsh and Prof. Dana . . . are both too busy to take a hand, but Prof. Sumner is coming in, probably for a week from next Sunday, that is a week after we print the article. Won't you stir up Powell and Cope or any of the other combatants you may have in mind and get them to send in their contributions promptly? It is a good thing to have King's article appear on the same day with Sumner's by way of ballast, can you get him? For Sunday, the 30th. None of them need sign the articles unless they wish, though we should prefer signatures.
William Graham Sumner, a Yale sociologist, was probably the leading exponent of Social Darwinism in the U.S., and could be counted on to give strong support to the mechanistic principles that Spencer preached—but apparently Sumner never came through with a contribution. The Powell that Miller wanted was Peirce’s friend John W. Powell, Director of the U.S. Geological Survey, but he did not enter the debate either. He wrote to Peirce that he would like to join in but did not have the time. King must have been Clarence King, the geologist who advanced the theory that catastrophes and cataclysms are important factors in evolution, particularly with respect to rapid evolutionary developments. King may have contributed as "Kappa."
The debate opened on 23 March with an introductory editorial and a piece by Peirce, "Herbert Spencer's Philosophy. Is it Unscientific and Unsound?" (sel. 45), and was framed as a set of questions, but the tone was such as to raise the temperature of Spencer supporters. For example, Peirce took Spencer's recommendation that a good way to make intellectual progress was to compare competing opinions and settle on those that survive mutual cancellation, as an occasion to ask: "Are thinkers ever really obliged to give all opinions equal votes . . . ?" He pointed out that there are some things—matter, space, time, law—which Spencer's "somewhat clumsy conception of evolution has left him no room to explain in any evolutionary sense." Spencer claimed that these "inexplicables spring directly from the Unknowable" but, Peirce asked, is this resort to the Unknowable really "thoroughgoing evolutionism"? Finally Peirce explained that since Spencer's intention was to produce "a great scientific theory, a philosophy worthy to form the crown of modern science"—Spencer's own "guess at the riddle"—it should be evaluated by "the recognized touchstone of a scientific theory": successful prediction. What scientific discoveries, Peirce wanted to know, can be attributed to Spencer's synthetic philosophy? Almost at once, after his opening article appeared, Peirce wrote to Miller asking to be paid. Miller replied that "checks for contributions to The Times are made out on Fridays" and he added: "I hope you will stir up as many combatants as possible and promptly."
Peirce stayed on the sidelines for the following two Sundays while the first seven respondents weighed in, but he contributed a second article on 13 April: "`Outsider' Wants More Light" (sel. 47). Claiming once again that he was only seeking light— "an attack would be very different"—he replied to all seven respondents, but principally to three who had tried to answer from the standpoint of science. Henry Osborn, a well-known paleontologist, received Peirce’s most serious and polite reply. Peirce drew support from Osborn for his "doubt" that Spencer's work would have permanent value. He treated Hiram Messenger and Edgar Dawson much less respectfully, essentially ridiculing them; his intent throughout was to stir up interest and emotions to keep the series going. Peirce did raise two or three interesting points that he would develop more fully in later years. In response to Messenger's claim that he could find no mathematical errors in Spencer's extensive writings, Peirce gave a single example. Spencer claimed that all phenomena are "necessary results of the persistence of force." Peirce pointed out that it would be perfectly consistent with the principle of the persistence of force if at any given moment all the molecules in the universe were assumed to be in their actual positions but with reversed velocities. From that moment on, history would run in reverse. But "eggs grow into birds, not birds back to eggs," so clearly not all the phenomena of evolution can be mathematical consequences of the persistence of force. In response to "Kappa," Peirce outlined the seven tasks that have to be performed by a good critic of philosophy. That was a subject that would interest Peirce for the rest of his days. In response to "R.G.E." he made the interesting observation that his dissatisfaction with Spencer "is not that he is evolutionist, but that he is not evolutionist enough."
Peirce’s use of the pseudonym "Outsider" for his contributions to this debate may have been partly a ploy to add an air of mystery to the proceedings but it was also intended to situate Peirce outside the prevailing ethos of Social Darwinism. When Miller introduced the debate he indicated that the pseudonym allowed "Outsider" to "stand apart from the adepts whom he calls upon to speak their minds." He added, however, that the name, "Outsider," was really too modest for "he is himself eminent for his attainments in science and might speak with some authority upon the questions he raises." But it may be that Peirce’s use of a pseudonym was not so much to set himself apart from his respondents as it was a prudent decision based on his understanding that he could no longer pretend not to be standing apart and that his own name might keep some interested parties from participating. That he chose the pseudonym "Outsider" may have been Peirce’s wry way of stating an unpleasant truth.
Around the same time Peirce took up the cause against Spencer, perhaps a few weeks before, he arranged with Lorettus Sutton Metcalf to contribute to a series of articles on spiritualism Metcalf was organizing for his journal, The Forum. Peirce was known to be a skeptic concerning such matters, especially because of his recent dispute with Gurney, and Metcalf had engaged him to present a case against spiritualism. It is not known whether Peirce sought out Metcalf to offer his services, or whether Metcalf had become aware that Peirce was looking for magazine work, but it is likely that it was not until after the first article in the series had appeared that Peirce struck his deal with Metcalf. The first in the series was a piece by Mary J. Savage entitled "Experiences with Spiritualism," which appeared in the December 1889 issue. The second, "Truth and Fraud in Spiritualism," by Richard Hodgson, appeared in April 1890. Peirce’s article was to follow. It was never given a title by Peirce, but for the present volume the editors have entitled it "Logic and Spiritualism" (sel. 44). It could also have been called "The Case against Spiritualism."
Initially Peirce must have thought he would make an easy go of this assignment, for he had worked through the arguments quite thoroughly during the Gurney controversy. But by the end of March he had run into a snag. His first draft ran to 6700 words and Metcalf had set a limit of 5000. Metcalf would not budge and Peirce was equally determined to say everything he wanted to say, so there ensued a curious battle of wills. Peirce finally conceded to Metcalf's word limit, probably because he was in such great need of the remuneration, but Metcalf had to agree to Peirce’s peculiar way of cutting his article down to size. Peirce simply struck out hundreds of articles and pronouns transforming his paper into something not quite a poem but not really prose either. Peirce’s paper was set in galleys on 7 April, but he continued making revisions. He could not make it work and asked if he could start over. Metcalf agreed but asked Peirce to hurry it up and "please remember not to exceed 5000 words" (21 June 1890). Peirce never rewrote the paper. 57 Back in Quicktown, after Juliette's return from Europe, other priorities had taken center stage.
Peirce began his essay by admitting that he was a man of science—a scientific specialist—and made it plain that he believed that "no mind with which man can communicate can act or feel otherwise than through its residential nerve-matter." But he did not doubt that "unrecognized avenues of sense may exist" and he believed that telepathy was not an impossibility. Nevertheless, he thought that science had to reject spiritualism and telepathy as viable hypotheses to explain unusual and unexpected phenomena. His argument against spiritualism is complex and cryptically stated because of the many revisions and cuts his manuscript had suffered. Important for his argument are three assumptions which he believed psychology had sufficiently established: 1. The obscure part of the mind is the principal part. 2. It acts with far more unerring accuracy than the rest. 3. It is almost infinitely more delicate in its sensibilities. It is this vast "unconscious or semi-conscious" part of the mind, which evolves through generations of interaction with external forces into instinct and common sense, which must be trusted to guide us in situations where reason does not know which way to turn. This is our "mother-wit" which, for all we know, may have access to the "unrecognized avenues of sense." The secret of mother-wit is that over the course of her education, her evolution, she has "learned" to follow nature's laws—nature's reason. Now the general conclusions of mother-wit, our common sense, should not be dismissed in the face of some "special experience." It is barely possible, of course, that any given strange occurrence might be an exception to law, a rebuff to common sense. But, generally, where there is a strange occurrence, the probability of a trick is greater than the likelihood that it is an exception to law.
After further development of his argument, Peirce looked back to Gurney's attempt to prove telepathy by amassing favorable cases and proclaimed that "the myriad strange stories prove nothing." Such supposed evidence for telepathy or spiritualism loses its force when we consider four simple facts: 1. "the fact that all men are liars"; 2. "the fact of deranged imagination, hypnotism, hysteria"; 3. "the fact that we may receive and act upon indications of which we are quite unconscious"; and 4. "the fact that a certain number of coincidences will occur by chance." Taken together, these facts serve as a basis for explaining unusual and surprising perceptions without resort to ghosts or spirits. In an earlier draft Peirce wrote: "why should we draw upon such an extreme rarity as telepathy, so long as we have such ordinary elements of human experience as superstition, lying and self-lying (from vanity, mischief, hysteria, mental derangement, and perverse love of untruth), exaggeration, inaccuracy, tricks of memory and imagination, intoxication (alcohol, opiate, and other), deception, and mistake, out of which to shape our hypotheses?"
In his final paragraph, Peirce made it clear that he was not dismissing the importance of psychical research; on the contrary, it "should receive every encouragement." But properly conducted, it would become a branch of experimental psychology—the branch of science "destined to be the most important experimental research of the twentieth century." Even though this paper remained unpublished, some of the ideas would make their way into the fourth article of Peirce’s Monist metaphysical series, "Man's Glassy Essence"; that series would, in fact, reverberate with ideas from this period, especially ideas from "A Guess at the Riddle" and the Outsider pieces.
Working out definitively how the writings in this volume contributed to the overall development of Peirce’s thought is a task for the community of scholars who will study them for that purpose, but a few additional thoughts might be helpful. Following again the method used in the introduction to W5, it may be revealing to consider how the W6 writings fit into Peirce’s general intellectual development as traced by Murphey and Fisch. 58 According to Murphey, the most telling demarcations in Peirce’s intellectual development are revisions to his system of categories necessitated by discoveries in logic. For Fisch, the single most important gauge of the growth of Peirce’s thought was its movement toward the robust three-category realism of his later years.
Murphey divides Peirce’s intellectual life into four phases dominated in turn by Kant's system of philosophy, by syllogistic logic, by the logic of relations, and by the logic of quantification. According to Murphey, the fourth and final phase began about 1885 after Peirce, with his student O. H. Mitchell, discovered the quantifier. Only then could Peirce add pure indexical signs to his logic, signs that refer to individuals per se and not to conceptions. The individual, the non-general, quickly took on a special importance for Peirce as he came to realize that a non-conceptual acquaintance with individuals can provide a direct and immediate link to reality. According to Murphey, this allowed Peirce to retreat from the conceptualism of his "end of inquiry" theory of reality without having to resort to "first impressions of sense." 59 Although Murphey makes the long final period of Peirce’s intellectual development range over the last three decades of Peirce’s life, he does notice that around 1896 Peirce formed a new conception of the continuum after discovering that continua must involve unactualized possibilities: "Whatever is continuous therefore involves real possibility and is accordingly of a general nature." 60 Murphey notes that Peirce announced this discovery to William James in March of 1897 and that it led to a strengthening of Peirce’s realism. It is surprising that Murphey did not count the period following this important logical insight, the period of Peirce’s synechism— "the new Scholastic realism" 61 —as a new and final phase of Peirce’s development, one dominated by modal logic (and by Peirce’s Existential Graphs).
In Fisch's account, Peirce’s thought is shown to have developed gradually from an early nominalism that attributed generality only to cognitions and that held all realities to be "nominal, significative, cognitive" (W2:181), to a robust form of realism that gave ontological place to each of the three categories. Fisch marks the major stages of Peirce’s intellectual journey by three principal revisions to his ontology: his acceptance, beginning around 1868, of "the long run" as providing an independence condition for reality; his admission, around 1890, that reality extends to the non-cognitive realm of actuality; and his admission in 1897 that even possibility is real. In line with Murphey's understanding of the importance of Peirce’s logical discoveries of the mid-1880s, Fisch notes that Peirce had taken large strides toward acknowledging the reality of secondness with his 1884-85 acceptance of the necessity of indexes for logic and his 1885 reaction to Royce's idealism (W5: sels. 30, 33), but he believes it was not until about 1890, when he accepted Scotus's haecceities, that he saw that ultimate reality should be ascribed to seconds. 62 It seems likely, however, that Fisch's principal reason for locating this important intellectual event in about 1890 was his belief, following Hartshorne and Weiss, that Peirce’s "A Guess at the Riddle" had been composed then. It was there, in the chapter on physics, that Peirce stated clearly for the first time that what "Scotus calls the hæcceities of things, the hereness and nowness of them, are indeed ultimate" (p. 205). But it now seems much more likely that Peirce composed that important chapter as early as 1887 or 1888, and that he had started his "Guess," as "One, Two, Three," by 1886. These considerations, as well as the many references to the necessity of indices for logic, beginning as early as 1881 (W4:251), and his work, beginning as early as 1886, on definitions for "haecceity" and "scotism" for the Century Dictionary (see W5:389), all suggest that Peirce’s acceptance of the reality of secondness is better dated "around 1887" than "around 1890." Accordingly, the step to Murphey's fourth phase and Fisch's second stage occurred near the beginning of the years covered by the present volume so that the writings in W6 may be viewed as inaugurating what Fisch calls Peirce’s period of two-category realism.
Fisch's account of Peirce’s journey from nominalism to a robust realism has been challenged by a number of scholars, including Don D. Roberts, Fred Michael, and, most recently, T. L. Short. Roberts argued in 1970, soon after Fisch's account first appeared, that there is no compelling reason for concluding that Peirce ever was an out and out nominalist and that it would be safer to conclude that he was always a realist. Roberts accepted, however, that there were nominalistic elements in Peirce’s thought. 63 Michael agrees with Fisch that Peirce was at first a nominalist, but argues that his nominalism continued until the mid-1880s, when he became a realist by taking the crucial step of accepting that there are singulars outside of cognition—what Fisch identifies as accepting the reality of secondness. Earlier declarations of realism were, at most, nominal. 64 Short, the most recent dissenter to Fisch's account, argues that in at least one important sense, Peirce remained a nominalist all his life, namely, in his "continuing inclination toward a `nominalism' that identifies reality with a world external to cognition." Peirce’s "nominalism," rather than something to be overcome, was an important component of Peirce’s realism, actually contributing to its depth. 65 These are valuable studies, each contributing important insights concerning Peirce’s development as a philosopher, and the disagreements, though going much deeper, serve to highlight the difficulty in reaching consensus on the meaning of "nominalism" and "realism" and on what constitutes a significant change with respect to these two positions. But whatever labels they use, these scholars all agree that there was a significant development within Peirce’s thought and that the repercussions that followed his introduction of logical quantifiers in the mid-1880s clearly constitute one of his major periods of change. Another would come around 1897 when he accepted that there are generals external to thought, a change that would breathe new life into his slumbering pragmatism.
Thus the present volume, most notably with "A Guess at the Riddle" (sels. 22-28), inaugurates a new period of philosophy for Peirce, one distinguished by a commitment to a thoroughgoing architectonic approach based on his categories. The difficult task of reforming his entire system of thought, always with an eye for improving it, would occupy Peirce for the remainder of his life. Having accepted the reality of seconds, Peirce could begin to build an account of perception that would make sense of direct acquaintance with reality and that would provide reason to hope that inquiry could be guided toward the truth by the obstinacy of reality rather than by a conception of it. In his definition of "real" for the Century Dictionary, Peirce distinguished between "real objects . . . external to the mind," which are "independent altogether of our thought," and internal objects which "depend upon thought," though "not upon thought about them." By 1903, this distinction became a basic feature of his semeiotic (EP2:276) and by 1906 it had turned into the now familiar dynamical object/immediate object duo (EP2:477).
Among the other noteworthy ideas that seem to have originated or come much more clearly into focus during this period, we find in Peirce a growing conviction that instinct and evolutionary attunement to the laws of nature—to the "objective reason embodied in the laws of nature"—give humans a predisposition for guessing nature's laws (sels. 8, 15) and explain the importance of common sense (sel. 44). Peirce’s intensive work on reduction of observational data and modeling of hydrodynamic effects for his gravity reports, and perhaps even his critique of the design of Gurney's "experiment" to prove telepathic phenomena (sels. 16, 18), strengthened his conviction that probable reasoning is "the logic of the physical sciences," as he proclaimed in his definition of "probability" in the Century Dictionary. We find Peirce placing more stress on regulative principles, perhaps a step toward his later recognition of the normativity of logic, and on intellectual hopes (see sel. 28 and W5:221-34). There is an indication in some of the W6 writings that Peirce has begun moving toward his later accommodation with religion and his innovative theological ideas (sels. 14, 22, 23, 44). In science, including even his work for the Coast Survey, Peirce’s interest shows a definite turn toward dynamic and process-oriented concerns and, also, toward foundational and cosmological questions (sels. 25-28, 31, 36). Peirce reveals a timely grasp of the crisis that was developing in physics at the end of the 19th century 66 and perceptively recommended that progress would depend on a better understanding of physical matter at the molecular level and on fruitful new theories (sels. 28, 31). Peirce offered his "guess" as a candidate for a new paradigm in physics and began a book intended to promote and justify its embrace (sel. 31).
Peirce’s 1887 polemic against Herbert Spencer's "mechanical notion of the universe" (sel. 14) provided his first occasion for stating his case against the doctrine of necessity, 67 and turned him into a public critic of necessitarianism, even a prophet of its doom. Peirce’s aggressive rejection of mechanical causation as adequate for the explanation of growth and development, forced him to defend a teleological form of evolution and moved him in the direction of a theory of sign action, or semiosis. Peirce’s "guess at the riddle," as expressed about 1888, was that "three elements are active in the world: first, chance; second, law; and third, habit-taking"; there was not yet any explicit inclusion of signs among the basic components of the universe. But he was already committed to a close analogy between the growth of mind and the growth of physical law and he would make that connection explicit in 1892 when he proclaimed his tychistic thesis that matter is specialized or "effete" mind (R 972; see also, EP1:312). At least by 1907, Peirce would recognize that the end of semiosis of the highest kind is an intellectual habit, which realization may lead us to wonder whether the third basic element that is active in the universe, habit-taking, is a form of semiosis, and if that is what imparts the teleological current that Peirce finds in evolution.
In 1887, in a sketch of his "A Guess at the Riddle," Peirce noted that he wanted a "vignette of the Sphynx" placed below the title. 68 Then after stating his guess in Chapter VII, he added, "Such is our guess of the secret of the sphynx." On 5 April 1890, almost two years after he had put his manuscript aside, Jem wrote to him from Egypt: "I am now passing a few days on the edge of the desert & directly at the base of the Great Pyramid. It is by far the most stupendous structure I have ever seen, and the Sphinx is more imposing than I ever thought possible. . . . no calm that living man can experience approaches the sublime sweet god-like serenity of the sphinx under the full moon." Although Peirce’s Sphinx was no doubt the one of Greek mythology, Jem's letter would have moved him, and it must have been difficult not to take up his manuscript again; but he was working on "Logic and Spiritualism" for The Forum, and was still hard at work as the Outsider trying to raise money to send to Juliette in Europe. In July, Carus would invite him to contribute to his new journal, The Monist, and Peirce would take that opportunity to turn his "Guess" into the six articles known as the " Monist Metaphysical Series." That would appease his sphinx.
Nathan Houser
1. In writing this introduction, I have depended on the results of Max H. Fisch's many years of research, contained in his files and data collections at the Peirce Edition Project. To reduce the number of footnotes, I do not give references for items that can be easily located by keeping the following in mind: all references to manuscripts and Peirce family letters, unless otherwise indicated, are to the Peirce Papers in the Houghton Library at Harvard University; correspondence with employees of the Coast Survey is in Record Group 23 in the National Archives.
2. The Fisch Collection at Indiana University Indianapolis contains records of extensive research into Juliette's origin, primarily conducted by Maurice Auger, Victor Lenzen, and Max H. Fisch, but no final conclusions were drawn. Elisabeth Walther's Charles Sanders Peirce: Leben und Werk (Agis-Verlag, 1989), Joseph Brent's Charles Sanders Peirce: A Life (Indiana University Press, 1993; revised ed. 1998), and Kenneth Laine Ketner's His Glassy Essence (Vanderbilt University Press, 1998), each contain helpful discussions of Juliette's origin but do not settle the question.
3. See Thomas G. Manning's U.S. Coast Survey vs. Naval Hydrographic Office: A 19th-Century Rivalry in Science and Politics (University of Alabama Press, 1988), especially ch. 4, and his "Peirce, the Coast Survey, and the Politics of Cleveland Democracy," Transactions of the Charles S. Peirce Society 11 (1975): 187-94. Also see Brent, ch. 3, and the introduction to W5.
4. See Francis Ellingwood Abbot's Organic Scientific Philosophy: Scientific Theism (Boston: Little, Brown, & Co., 1885) and Josiah Royce's The Religious Aspect of Philosophy, A Critique of the Bases of Conduct and of Faith (Boston: Houghton Mifflin Co., 1885). For Peirce’s reviews of these works, see W5: sels. 33, 46. For a brief account of Peirce’s work for the Century Dictionary, leading up to 1887, see the Introduction to W5, pp. xliii-xliv. See also W5: sel. 57.
5. For some background remarks on Peirce’s involvement with the scientific assignment of the Greely expedition, see the introduction to W4, p. xxxi.
6. Greely to Thorn, 29 March 87. NARG 23.
7. In his published report (sel. 30), Peirce gave 10 to 15 grams as the probable weight loss, but in a 28 February 1887 letter to Thorn (NARG 23), he estimated that 15 to 20 grams had been lost.
8. Fisch, p. 229.
9. Around 1950, Alonzo Church discovered in Marquand's papers at Princeton a fairly elaborate circuit diagram for a logic machine, thus establishing that Peirce’s recommendation had been acted on. It is not known whether an electrical logic machine was built. Ken Ketner has argued that Peirce himself drew the wiring diagram, probably in 1887. See Ketner's article, with Arthur F. Stewart: "The Early History of Computer Design: Charles Sanders Peirce and Marquand's Logical Machines," The Princeton University Library Chronicle, Vol. 45, 1984, pp. 187-211. Alice and Arthur Burks discuss the Marquand diagram in Appendix A of The First Electronic Computer: The Atanasoff Story (University of Michigan Press, 1989), pp. 339-48, and conclude that it marks a significant advance in computing engineering theory—or would have had it become known. Although they do not believe that Peirce drew the elaborate circuit diagram, they do argue that it is plausible to credit Peirce with being the first to have conceived of an electrical general-purpose programmable computer, but they find no clear evidence that Peirce’s or Marquand's ideas had any influence in the development of electronic computing.
10. Manning (1988), p. 90.
11. Brent, pp. 171-2.
12. B. A. Colonna to George Davidson, 17 December 86. National Archives RG 23.
13. See Brent, p. 185.
14. See Brent, p. 186.
15. From Henry Leonard's notes of conversation with Mrs. Robert G. Barkley, Milford resident. Fisch Collection.
16. Brent, p. 187.
17. The Leopold Shakespeare. The Poet's Works in Chronological Order, from the Text of Professor Delius (London: Casser, Petter, & Galpin, 1877).
18. Charles Richet, "La suggestion mentale et le calcul des probabilités," Revue Philosophique de la France et de l'Étranger 18 (1884): 609-74. See Ian Hacking's "Telepathy: Origins of Randomization in Experimental Design," ISIS 79 (1988): 427-51, for an account of the circumstances giving rise to Phantasms, and the Peirce-Gurney dispute. Many of the details of this paragraph are taken from Hacking's article. Also see Stephen E. Braude's "Peirce on the Paranormal," Transactions of the Charles S. Peirce Society 34 (1998): 203-24.
19. See Hacking op. cit. and W5:xxv-xxvi.
20. Gurney, Myers, and Podmore were using the British system where a billion equals a U.S. trillion and a trillion equals, in U.S. terms, a billion billions.
21. Abstracts for these thirty-one cases, and others mentioned in selections 16-19, are available on the Electronic Companion for W6.
22. Hacking, p. 445.
23. All three papers appeared in The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science: Henry A. Rowland, "On the Relative Wavelengths of the Lines of the Solar Spectrum," vol. 23: 257-65; Louis Bell, "On the Absolute Wave-length of Light," vol. 23: 265-82; Albert A. Michelson and Edward W. Morley, "On a Method of making the Wave-length of Sodium Light the actual and practical Standard of Length," vol. 24: 463-66.
24. The article in Journal für die reine und angewandte Mathematik —referred to by Peirce as Crelle's Journal—has not been identified. It is clear, from Risteen's 4 Aug. 1887 letter, that Peirce had recommended a "demonstration," probably in an 1887 issue, in connection with the study of curves.
25. Peirce’s landmark 1881 paper, "On the Logic of Number" (W4:299-311) is discussed in the introduction and annotations to W4 (see especially pp. 575-76, annotation 222.24).
26. See Ernst Schröder's review of Frege's Begriffsschrift in Zeitschrift für Mathematik und Physik 25 (1880): 81-87, 90-94.
27. Peirce must have been referring to James's "The Perception of Space," which appeared in Mind, vol. 12, in four parts: I (Jan. 1887, pp. 1-30), II (Apr. 1887, pp. 183-211), III (Jul. 1887, pp. 321-53), and IV (Oct. 1887, pp. 516-48).
28. Philosophical Transactions of the Royal Society of London 177 (1886): 1-70.
29. Peirce’s "improvements" were presented to the Johns Hopkins Scientific Association and reported in Johns Hopkins University Circulars 1 (1880): 16. Kempe's paper, "On the Geographical Problem of the Four Colours," appeared in American Journal of Mathematics 2 (1879): 193-200.
30. For a treatment of Kempe's influence see Roberts (1973), pp. 20-25.
31. "Note to a Memoir on the Theory of Mathematical Form," Proceedings of the Royal Society 42 (1887), 193-96.
32. Lenzen to Fisch, 11 July 1961. Fisch Collection.
33. See the introduction to W5, pp. xxxix-xlii for a discussion of the influences on Peirce.
34. Fisch, p. 229.
35. A record of this interview is in the Fisch Collection.
36. Ferris Greenslet. The Lowells and Their Seven Worlds. Boston: Houghton Mifflin Co., 1946, p. 356.
37. Peirce estimated that he had been responsible for about 16,100 words (RMS 1163:2). For a more complete account see "Peirce’s work for the Century Dictionary " by Jeffrey R. Di Leo and André DeTienne, Peirce Project Newsletter 3 (1999): 1-2.
38. Simon Newcomb to William D. Whitney, 9 July 1889, Yale (Beineke).
39. William D. Whitney to Henry Whitney, 26 June 1889, Yale (Beineke).
40. Peirce did not mention Ann Arbor in this letter, but that was probably an oversight.
41. The National Archives "Register of Records" indicates that this report was received and stored as GO - 401, 902 HG in Box 395. It is now missing.
42. Brent, p. 195.
43. Victor F. Lenzen, "An Unpublished Scientific Monograph by C. S. Peirce," Transactions of the Charles S. Peirce Society 5 (1969): 5-24.
44. In his definition of "gravity" for the Century Dictionary, Peirce wrote: "The words gravity and gravitation have been more or less confounded; but the most careful writers use gravitation for the attracting force, and gravity for the terrestrial phenomenon of weight or downward acceleration which has for its two components the gravitation and the centrifugal force."
45. Lenzen (1969), p. 13.
46. Victor F. Lenzen and Robert P. Multhauf, "Development of Gravity Pendulums in the 19th Century," Contributions from the Museum of History and Technology (Smithsonian Institution, Bulletin 240, 1966), pp. 301-47.
47. Report of the Superintendent of the U. S. Coast and Geodetic Survey for the Fiscal Year Ending June 30, 1891, part II, Appendix no. 15, pp. 503-64.
48. See Lenzen (1969), pp. 6-7.
49. See Lenzen (1969), passim.
50. Peirce’s best value for gravity at the Smithsonian was 980.1037 cm/sec 2 , but that was not the value given in the 1889 report; it comes from a letter of 3 July 1890 from Peirce to Herbert Nichols, Professor of Physics at Cornell University. The value from the report is 99.095 cm (as the length of the mean equatorial seconds' pendulum), which converts to an acceleration slightly less than Peirce’s "best value." Lenzen points out, however, that the value given in the 1889 report had not been corrected for flexure, which may account for the difference (see Lenzen 1969: 17 - 20).
51. Lenzen (1969), p. 20.
52. See Brent, pp. 14-15, especially in revised edition.
53. This opinion was expressed in a private communication.
54. See De Tienne's "The Mystery of Arisbe," Peirce Project Newsletter 3 (1999): 11-12.
55. The first two lines of this letter of 22 April 1890 have been heavily crossed out. This reading is based on Max H. Fisch's study of the document.
56. See Brent, pp. 303-08.
57. See the textual editor's headnote to selection 44 (pp. 658-663) for further discussion of Peirce’s relations with Metcalf and the import on Peirce’s composition.
58. Max H. Fisch, Peirce, Semeiotic and Pragmatism, eds. K. L. Ketner and C. J. W. Kloesel, (Indiana University Press, 1986) and Murray G. Murphey, The Development of Peirce’s Philosophy, (Harvard University Press, 1961; Indianapolis: Hackett Publishing Co., 1993).
59. See Murphey, pp. 301-03.
60. Murphey, p. 396.
61. Ibid.
62. Fisch, p. 190.
63. Don D. Roberts, "On Peirce’s Realism," Transactions of the Charles S. Peirce Society 6 (1970): 67-83.
64. Fred Michael, "Two Forms of Scholastic Realism in Peirce’s Philosophy," Transactions of the Charles S. Peirce Society 24 (1988): 317-48.
65. T. L. Short, "Review Essay," Synthese 106 (1996): 409-30.
66. See Murphey, pp. 327-48.
67. Fisch, p. 229.
68. It is commonly believed that Peirce’s allusion to "the riddle" and his reference to the Sphinx were beholden to Emerson's poem, "The Riddle of the Sphinx." But the story is more complicated: see the introduction to W5, pp. xli-xlii and annotation 165.title in this volume on pp. 438-39.
Original readings are given in brackets after the correction.
1 July ’67 [1 Dec.] line to be moved after l. 21 in Chronology
26 Apr. [30 Apr.]
27 Nov. [Nov. 27]
30 [3]
ab:d̅ and ac :d̅, [ab:d and ac:d,]
a̅ + c̅ + d̅ [a̅ + c̅ + d]
a̅ + d̅ + d̅, or a̅ + d̅ [a̅ + d + d, or a̅ + d]
but when n = -∞ [but when n = ∞ ]
tickets seem [tickets seems]
ann. [ann] Also 435.1, 462.31, 470.1, 473.42
of the Peirces’. [of the Peirces.]
measurement [measument]
proceeded [proceded]
are wrong [is wrong]
Rogers] William Augustus Rogers (1832–1898), Assistant Professor of Astronomy at Harvard College Observatory until 1886 and subsequently Professor of Physics and Astronomy at Colby University, Waterville, Maine [Fairman Rogers ... of Sciences.]
same as pair 3; [same as pair 2;]
See also textual note 369.2 p. 656. [See also textual note.]
in the third [in the the third]
Dawson’s [Dawsons’s]
Ptolemy [Ptolemy’s]
E; altero-alio [E; alter-alio]
⟡366.33 Necessitates priorit [366.33 Necessitates priority]
Selection 37 in W6: 354–56, titled [Reasoning], ends with three ellipsis points within italic brackets because the editors were unable to find the sheet(s) that continued its last leaf. We have identified that continuation, whose brevity made it hardly noticeable among the many fragments. It is found in R 579: 12, and consists of the following five words: “so, it is bad reasoning.” Readers of W6 are invited to enter this correction in their copy on p. 356, and to correct the corresponding entry in the Chronological Catalog in W6: 527 (c. 1889.1), whose first part needs to read: “Holograph, 8 sheets, Houghton, Peirce Papers, R 830: 2, R 278: 240, 243, 269, 268, 267, 266 (= R 1573: 250), R 579: 12; . . .”
Christopher R. Versen defended in 2006 at Florida State University a dissertation relevant to the controversy; it is titled “Optimistic Liberals: Herbert Spencer, the Brooklyn Ethical Association, and the Integration of Moral Philosophy and Evolution in the Victorian Trans-Atlantic Community.” A subsection of it (pp. 236–244) is devoted to an illuminating discussion of “The Outsider Controversy, March 23 to May 4, 1890” regarding the credibility of Spencer’s evolutionary philosophy Peirce had engineered in the New York Times (see selections 45 and 47). As a result of Versen’s dissertation, the following three annotations for selection 47 in W6 were expanded in their online version: annotations 407.1–2, 407.3–6, and 407.14, chiefly by way of identifying plausibly who were W. H. B., R. G. E., and Kappa. Versen’s signal contribution is to provide an essential intellectual and social background to the controversy, showing in particular the role played by the ultra-Spencerian Brooklyn Ethical Association in orchestrating replies from several of its members to Outsider.
That same dissertation reveals that Peirce subsequently published a brief note of thanks in the New York Times on May 4, 1890 (p. 2, bottom of column 7). Peirce is therein thanking William Jay Youmans (older brother of Edward L. Youmans) for the information the latter provided in his article titled “Mr. Spencer’s Rank as a Philosopher. A Formidable Array of Evidence in His Support—Metaphysicians, Biologists, Mathematicians, Physicians, and Learned Societies in Many Lands Pay Him Honor” (New York Times, April 27, 1890, 13). Youmans referred back to it subsequently in an article on “Mr. Spencer’s Place in Philosophy” in the journal he edited, the Popular Science Monthly 37 (August 1890), p. 552. Here is the transcription of Peirce’s note along with a screenshot of it.
To the Editor of the New-York Times:
I must beg the use of your columns once more, in order to thank Dr. Youmans for having demonstrated, as he clearly has, the profound respect in which Mr. Herbert Spencer is held by men of science the world over and for having shown that he has received high scientific honors, which, however, his own conception of his position has forbidden him to accept. This, without of course sufficing to put his philosophy beyond doubt, does satisfactorily answer the question to which I gave special prominence.
OUTSIDER.
 New York Times, 4 May 1890, p. 2, col. 7
New York Times, 4 May 1890, p. 2, col. 7
“If thinkers will only be persuaded to lay aside their prejudices and apply themselves to studying the evidences of [the doctrine of agapasticism,] I shall be fully content to await the final decision.”
Volume 8 of the Writings picks up the trail of Peirce’s writings where volume 6 ended, in May 1890, and follows it until the end of July 1892 (Peirce’s 1883–1909 contributions to the Century Dictionary form the content of volume 7). The absence of any scientific report in the volume attests to the unraveling of Peirce’s career at the U.S. Coast and Geodetic Survey: the tale of his final struggles with the Survey’s Superintendent, culminating in his resignation at the end of 1891, is vividly recounted throughout Nathan Houser’s introduction. The ending of a career that had brought him international reputation as a scientist threw Peirce’s life into turmoil. The loss of his principal source of income meant the beginning of permanent penury, and thus of daily strenuous but often futile efforts to find gainful employment: writing book reviews for the Nation, striking a deal with the Open Court Company for the serial publication of philosophical articles and for the production of an arithmetic textbook, improving a chemical process for bleaching paper (and getting swindled out of it), patenting several inventions, resurrecting a correspondence course in logic, entering the lecture circuit, applying for university positions or federal grants, and pursuing ill-conceived investment schemes. Peirce tried them all with much hope but ended up learning a hard spiritual lesson: he would have to forego material success to fulfill his destiny, one written in intellectual achievements purposed only for posterity.
The principal philosophical achievement heralded in the present volume is Peirce’s celebrated Monist metaphysical project, consisting of five classic articles that lay out the chief operative principles of an evolutionary cosmology resting on the reality of absolute chance (tychism), continuity (synechism), and love (agapism), relieved against the background of a three-category realism that ushers in Peirce’s objective idealism. Those five papers are published afresh along with four additional unpublished texts that enhance their understanding.
The volume includes also eighteen Nation reviews or essays in which Peirce critiques such authors as Paul Carus, William James, Comte, Lombroso, and Karl Pearson, or takes part in controversy, notably the famous dispute between Francis E. Abbot and Josiah Royce. Many other documents make here their first appearance: short philosophical essays that try out new ideas, studies in non-Euclidean geometry and number theory, further explorations of Boolean algebra and the algebra of the copula, studies of great men, classification of the sciences, and discussions of moral issues. Especially noteworthy is Peirce’s only known experiment in prose fiction, his sentimental tale “Embroidered Thessaly,” which recounts the adventures of a young man traveling through Thessaly in 1863.
“There is one moral quality without which a reasoner cannot escape fallacies, and that is a sturdy honesty of purpose.”
“If thinkers will only be persuaded to lay aside their prejudices and apply themselves to studying the evidences of [the doctrine of agapasticism,] I shall be fully content to await the final decision.”
Volume 8 of the Writings picks up the trail of Peirce’s writings where volume 6 ended, in May 1890, and follows it until the end of July 1892 (Peirce’s 1883–1909 contributions to the Century Dictionary form the content of volume 7). The absence of any scientific report in the volume attests to the unraveling of Peirce’s career at the U.S. Coast and Geodetic Survey: the tale of his final struggles with the Survey’s Superintendent, culminating in his resignation at the end of 1891, is vividly recounted throughout Nathan Houser’s introduction. The ending of a career that had brought him international reputation as a scientist threw Peirce’s life into turmoil. The loss of his principal source of income meant the beginning of permanent penury, and thus of daily strenuous but often futile efforts to find gainful employment: writing book reviews for the Nation, striking a deal with the Open Court Company for the serial publication of philosophical articles and for the production of an arithmetic textbook, improving a chemical process for bleaching paper (and getting swindled out of it), patenting several inventions, resurrecting a correspondence course in logic, entering the lecture circuit, applying for university positions or federal grants, and pursuing ill-conceived investment schemes. Peirce tried them all with much hope but ended up learning a hard spiritual lesson: he would have to forego material success to fulfill his destiny, one written in intellectual achievements purposed only for posterity.
The principal philosophical achievement heralded in the present volume is Peirce’s celebrated Monist metaphysical project, consisting of five classic articles that lay out the chief operative principles of an evolutionary cosmology resting on the reality of absolute chance (tychism), continuity (synechism), and love (agapism), relieved against the background of a three-category realism that ushers in Peirce’s objective idealism. Those five papers are published afresh along with four additional unpublished texts that enhance their understanding.
The volume includes also eighteen Nation reviews or essays in which Peirce critiques such authors as Paul Carus, William James, Comte, Lombroso, and Karl Pearson, or takes part in controversy, notably the famous dispute between Francis E. Abbot and Josiah Royce. Many other documents make here their first appearance: short philosophical essays that try out new ideas, studies in non-Euclidean geometry and number theory, further explorations of Boolean algebra and the algebra of the copula, studies of great men, classification of the sciences, and discussions of moral issues. Especially noteworthy is Peirce’s only known experiment in prose fiction, his sentimental tale “Embroidered Thessaly,” which recounts the adventures of a young man traveling through Thessaly in 1863.
“There is one moral quality without which a reasoner cannot escape fallacies, and that is a sturdy honesty of purpose.”
| Illustrations | x | |
| Preface | xi | |
| Chronology | xix | |
| Bibliographical Abbreviations in Editorial Matter | xxiii | |
| Introduction | xxv–xcvii | |
| 1. | Familiar Letters about the Art of Reasoning | 1 |
| 2. | Ribot’s Psychology of Attention | 13 |
| 3. | Six Lectures of Hints toward a Theory of the Universe | 17 |
| 4. | Sketch of a New Philosophy 19 | |
| 5. | [On Framing Philosophical Theories] | 23 |
| 6. | The Non-Euclidean Geometry Made Easy | 25 |
| 7. | Review of Jevons’s Pure Logic | 30 |
| 8. | Review of Carus’s Fundamental Problems | 33 |
| 9. | Review of Muir’s The Theory of Determinants | 36 |
| 10. | Review of Fraser’s Locke | 38 |
| 11. | [Notes on the First Issue of the Monist] | 42 |
| 12. | My Life | 44 |
| 13. | Note on Pythagorean Triangles | 47 |
| 14. | Hints toward the Invention of a Scale-Table | 48 |
| 15. | Logical Studies of the Theory of Numbers | 55 |
| 16. | Promptuarium of Analytical Geometry | 57 |
| 17. | Boolian Algebra | 63 |
| 18. | Boolian Algebra. First Lection | 69 |
| 19. | Notes on the Question on the Existence of an External World | 78 |
| 20. | [Note on Kant’s Refutation of Idealism] | 80 |
| 21. | [Notes on Consciousness] | 81 |
| THE MONIST METAPHYSICAL PROJECT | ||
| 22. | The Architecture of Theories [Initial Version] | 84 |
| 23. | The Architecture of Theories | 98 |
| 24. | The Doctrine of Necessity Examined | 111 |
| 25. | The Law of Mind [Early Try] | 126 |
| 26. | The Law of Mind [Excursus on the Idea of Time] | 130 |
| 27. | The Law of Mind | 135 |
| 28. | [Notes for “Man’s Glassy Essence”] | 158 |
| 29. | Man’s Glassy Essence | 165 |
| 30. | Evolutionary Love | 184 |
| STUDIES ON THE ALGEBRA OF THE COPULA | ||
| 31. | [Deductions from a Definition of the Copula] | 208 |
| 32. | Algebra of the Copula [Version 1] | 210 |
| 33. | Algebra of the Copula [Version 2] | 212 |
| 34. | Examination of the Copula of Inclusion | 217 |
| 35. | On the Number of Dichotomous Divisions: A Problem in Permutations | 222 |
| 36. | Methods of Investigating the Constant of Space | 229 |
| 37. | James’s Psychology | 231 |
| 38. | [Morality and Church Creed] | 240 |
| 39. | Review of Spencer’s Essays | 242 |
| 40. | Abbot against Royce | 245 |
| 41. | Review of Chambers’s Pictorial Astronomy | 248 |
| 42. | [Lesson in Necessary Reasoning] | 251 |
| 43. | The Great Men of History | 258 |
| 44. | The Comtist Calendar | 267 |
| 45. | The Non-Euclidean Geometry | 271 |
| 46. | The Sciences in Their Order of Generality | 275 |
| 47. | The Man of Genius | 277 |
| 48. | The Periodic Law | 284 |
| 49. | Keppler | 286 |
| 50. | [Plan for a Scientific Dictionary] | 292 |
| 51. | Embroidered Thessaly | 296 |
| 52. | [Why Do We Punish Criminals?] | 341 |
| 53. | Review of Buckley’s Moral Teachings of Science | 345 |
| 54. | Review of Ridgeway’s The Origin of Metallic Currency | 349 |
| 55. | Review of Pearson’s The Grammar of Science | 352 |
| 56. | Review of Curry’s The Province of Expression | 355 |
| Editorial Symbols | 359 | |
| Annotations | 362 | |
| Bibliography of Peirce’s References | 470 | |
| Chronological Catalog, May 1890–July 1892 | 480 | |
| Supplementary Catalog Entries | 511 | |
| Essay on Editorial Theory and Method | 515 | |
| Textual Apparatus | 532 | |
| Headnotes, Textual Notes, Emendations, Rejected Substantives, Alterations, Line-End Hyphenation | ||
| Line-End Hyphenation in the Edition Text | 679 | |
| Index | 681-724 |
The introduction originally printed in W8 was abridged by André De Tienne because of space limitations. In writing this introduction, [Houser] made heavy use of the Max H. Fisch files and data collections at the Peirce Edition Project. Footnote references are not given for items that can be easily located by keeping the following in mind: all quotations from manuscripts and Peirce’s letters, unless otherwise indicated, are to the Peirce Papers in the Houghton Library at Harvard University or in the Open Court collection; correspondence with members of the Open Court is in the Open Court collection in the Morris Library at Southern Illinois University; letters used are also from these collections or from the Coast Survey collection in the National Archives. Readers should consult the annotations and the textual notes at the back of the volume for additional information about circumstances related to the composition of the volume’s selections. This introduction continues those to the previous volumes and assumes their acquaintance in order to minimize repetitions.
What follows is an excerpt from the abridged version of W8's published introduction.
To download the entire, unabridged introduction as a pdf, click here.
The period from the spring of 1890 into the summer of 1892 was a time of emotional turmoil for Peirce, a time of rash ventures and dashed hopes that would culminate in a transforming experience and a new sense of purpose. In the previous decThe period from the spring of 1890 into the summer of 1892 was a time of emotional turmoil for Peirce, a time of rash ventures and dashed hopes that would culminate in a transforming experience and a new sense of purpose. In the previous decade, Peirce had suffered the loss of his teaching appointment at Johns Hopkins University and the stripping away of his leadership in gravity determinations for the U.S. Coast & Geodetic Survey. He and Juliette had left New York for Milford, Pennsylvania, in 1887, hoping to find acceptance in Milford’s thriving French community. By the time he turned fifty, Peirce had been pushed from center stage and his native sense of entitlement had been crushed. When in the spring of 1890 he helped organize a debate in the pages of the New York Times on the soundness of Herbert Spencer’s evolutionary philosophy, he signed his contributions with the pseudonym “Outsider,” reflecting his increasing estrangement from mainstream society.
Diagnosed with tuberculosis, Juliette went abroad in November 1889 to escape the cold northeastern Pennsylvania winter. During most of the winter and spring of 1890, while she convalesced in Cairo and in various Mediterranean port cities, Peirce stayed in New York City where he looked for opportunities to supplement his income. Peirce’s relations with Juliette had never recovered from the blow of his termination from Johns Hopkins in 1884 which had plunged the newly married couple into the first of many financial crises. For a while after their move to Milford things looked up, especially after their finances were augmented with inheritances from the estates of Peirce’s mother and his Aunt Lizzie. Charles and Juliette had been accepted into the high society of Milford, primarily the social circle that revolved around the prominent Pinchot family, and they were determined to live accordingly. By the end of 1889, the Peirces had invested nearly all of their assets in the old John T. Quick homestead, “Wanda Farm” (or “Quicktown”), and in surrounding woodland, altogether amounting to nearly 2000 acres. They had risked everything on the prospect of generating a good income from their new estate, from farming and from harvesting the timber and other natural resources, and perhaps from turning the old Wanda Farm, on the banks of the Delaware River, into a grand resort. This would have been a good plan had a projected bridge been built at Port Jervis to bring through a rail line from New York, but the bridge project failed and the Peirces ran out of reserves too soon to have any chance of success.
After his separation from Johns Hopkins in 1884, Peirce’s principal source of income was the Coast & Geodetic Survey, but he also drew significant supplemental pay for his work on the Century Dictionary and Cyclopedia as the contributing editor in charge of definitions in the fields of logic, metaphysics, mathematics, mechanics, astronomy, and weights and measures. But Peirce’s income from the Century Company did not make up for the loss of his salary from Johns Hopkins and, to make matters worse, Peirce was well aware that his position with the Survey was at risk. He therefore tried his best to add to his income. He convinced Wendell Phillips Garrison, the editor of the Nation, to give him more books for review and, during the period covered by this volume, over three dozen reviews or notes by Peirce appeared in the Nation (many duplicated in the New York Evening Post). Garrison paid Peirce well for his contributions and he proved to be a crucial source for supplementing Peirce’s income for several years to come. Peirce tried to form dependable connections of this kind with other periodical publishers (Charles R. Miller, Editor-in-Chief of the New York Times, and L. S. Metcalf, editor of the Forum) but with little success. Desperate for additional funds, he sought loans from friends and acquaintances and he tried his hand at inventions and various investment schemes, with no luck. He was constantly on the lookout for opportunities to market his expertise. He was for instance a regular patron of the Astor Library, New York’s largest reference library (in 1895 it would be consolidated to form the New York Public Library). Sometime in May 1890 he presented the library with a detailed list of missing “works on mathematical subjects” which he thought especially important and he offered to continue his efforts, probably hoping to be a paid consultant. His offer was declined; on 4 June 1890, he received a letter from Trustee Thomas M. Markoe thanking him for his “very full & valuable list” but letting him know that he “need give [him]self no further trouble about the matter.”
In May or early June 1890 Juliette arrived back in New York and the Peirces returned to their Pennsylvania home. Their return to Wanda Farm freed Peirce for a time from the daily hustle and allowed him to refocus his priorities. His work for the Coast Survey and the Century Company was the most pressing.
The Century Dictionary, hailed as the “most conspicuous literary monument of the nineteenth century,” was not only a dictionary of historical and common English usage but was distinguished by its comprehensive inclusion of scientific terms and was said to embody “the scientific spirit and work” of its time. Peirce had been recruited for the dictionary project while still teaching at Johns Hopkins and had begun drafting definitions as early as 1883, but his most intensive and sustained work began around 1888, when he began receiving proofs, and ran at least until the fall of 1891, when the first printing of the dictionary was completed. The first edition ran to 7,046 large quarto pages, included nearly half-a-million definitions for over 215,000 words, and as a measure of its encyclopedic scope was reported to contain “from a printer’s point of view” two-thirds as much information as the Encyclopedia Britannica. Even after the Century Dictionary was published, Peirce continued with his lexicographical work, writing corrections and new definitions in his interleaved copy and hoping to be paid on a per-word basis for a supplement that would eventually appear in 1909. Peirce would also look for other dictionary work and would propose various lexicographical projects. As the Century was nearing completion, Peirce tried for a position with Funk & Wagnalls to help with their famous single-volume Standard Dictionary, which would appear in 1894, and in 1892 he would draw up a “Plan for a Scientific Dictionary” that would provide a summary of human knowledge in 1500 pages (sel. 50). It is hard to overstate the importance of Peirce’s lexicographical work, not only for the income it produced but especially for its impact on Peirce’s intellectual development.
In July 1889 Thomas Corwin Mendenhall was appointed Superintendent of the U.S. Coast and Geodetic Survey. His predecessor, Frank M. Thorn, was a lawyer with no scientific training who had been appointed four years earlier to reform the Survey. In contrast, and to the relief of many government scientists, Mendenhall was a trained scientist and was expected to restore the Survey’s leadership in scientific research; certainly that was Peirce’s hope. Peirce’s career had been dedicated to advancing the theoretical foundations of geodetic science and his field work had always been conducted with the greatest care, using the most refined instruments, so that his results could contribute not only to the immediate practical needs of economic and social life but also to the growth of the science. Under his leadership, American gravity research took its place alongside the best gravity research in Europe. But the turn away from pure research that the Survey had taken under Thorn could not be reversed in the political and economic climate of the times and Peirce and Mendenhall soon reached an impasse.
...
Nathan Houser
Original readings are given in brackets after the correction.
1 July ’67 [1 Dec.] line to be moved after l. 21 in Chronology
* The Open Court was a biweekly in 1887, a weekly from 1888 to 1896, and a monthly thereafter.
The text of “The Doctrine of Necessity Examined” in W8: 113, lines 15–17 reads as follows:
For it is manifest that no universal principle can in its universality be compromised in a special case or can be requisite for the validity of any ordinary inference.
The word “compromised” was corrected into “comprised” in EP1: 300 (see annotation #6 for selection 22 in EP1: 385). The word “compromised” is Peirce’s original wording, which neither he nor Open Court editors corrected in subsequent galleys and proofs. Context suggests that Peirce did intend the word “compromised”: Peirce means that special cases cannot on their own compromise the universality of a universal principle. This is supported by the example he provides just afterward: “To say, for instance, that the demonstration by Archimedes of the property of the lever would fall to the ground if men were endowed with free-will, is extravagant;” (W8: 113, our emphasis). The universality of a physical principle cannot be compromised in a case that does not fall within the range of its applicability, nor can it be called upon as a decisive premiss to support some ordinary argument.
An entry numbered 2.5 ought to be added under the 1891 entries p. 488 just after the second “Architecture of Theories” entry, as follows. A transcript of that article is found here: P464.
2.5 The ‘Pons Asinorum’ Again. Mr. Peirce sets forth the History of the Phrase from the Times of Duns Scotus’s Followers.”
P 464. New-York Daily Tribune, (Tuesday, 6 January), p. 14, col. 5. This is a response to several articles which were critical of Peirce’s account of the phrase in the Century Dictionary. Those earlier articles are in the same newspaper at: O399, Friday 19 December 1890, p. 10, col. 2; O400, Tuesday 23 December 1890, p. 16, cols. 5-6; and O463, Friday 2 January 1891, p. 5, col. 5.
* served from 2004 to 2006
**served until September 2000
“The validity of a conception consists in the impossibility of reducing the content of consciousness to unity without the introduction of it.”
Volume 1 of The Essential Peirce provides scholars, teachers, and students with convenient access to the philosophical milestones Peirce achieved in his early to middle years. It begins with a text Peirce considered to be, from the moment it was written to the end of his life, his most historically significant philosophical achievement: “On a New List of Categories.” Some contemporary scholars dispute Peirce’s own assessment, because after all it is not as though Peirce’s thought did not increase in power and sophistication in ensuing decades. It remains, however, that that text is traversed by many fundamental insights regarding the general structure of any thought process or train of inquiry that will never be significantly altered. It resorts to methods of analysis and inference deeply aware of their limits and potentials, and opens up a new program of logical research that leaves in the dust the entire history before it while acknowledging at the same time everything it owes to its forebears. Students of the “New List” who manage to really understand, at a deep level, at least its major leading ideas, are set to far better understand everything else that Peirce wrote in later life, especially when it pertains to phenomenology and semiotics, but also much more.
The three subsequent texts from the Journal of Speculative Philosophy prolong many logical, epistemological, and metaphysical consequences emerging from the “New List.” They demonstrate the logical impossibility of unmediated cognition (or intuition), thereby establishing the primacy of mediated processes that are all based on three major classes of signs that will later be called iconic, indexical, and symbolical. They insist on the fundamental continuity of all processes of inquiry, thereby casting any type of dualistic reductionism into the bin of irredeemably simplistic explanatory temptations. They redefine inferential processes (deduction, induction, hypothesis) in the light of probabilities theory and generalize their structure in novel semiotic terms. They reinterpret sensations, feelings, emotions, perceptions, conceptions in the light of those same new logical insights. They redefine the whole of reality in terms of that which is not detached from but actually fuels the entire process of inquiry, so much so that reality and inquiry cannot be separated from one another. They usher in a new sort of idealism that accompanies a reinvented scholastic realism that soars above nominalism without slaying the latter, but restoring it back to its proper place. They also proclaim a new sort of community, one that transcends any finite conception thereof because its identity is defined by a purpose that aims at the indefinite increase of knowledge. They suggest a brand-new conception of humanity and personhood, as holistic as it is semiotic. They demonstrate that it is possible to hold a consistent theory of the validity of the laws of ordinary logic, and show how it is that the “social principle is rooted intrinsically in logic.”
Peirce’s review-article of Fraser’s Berkeley is an occasion for him to reflect on the relevance of metaphysics and its history in his own time, of wondering about the origin of the odd blend of Platonism and nominalism in Berkeley’s philosophy, and of exposing that origin in medieval metaphysics from the eleventh to the fourteenth century. His main thesis is that reality can be seen from two distinct points of view, those of nominalism and realism, and that this difference yields enormous epistemic and ontological consequences. Peirce comes down of course on the side of realism, which is a “highly practical and common-sense position.” His discussion of Duns Scotus and Ockham, and of how nominalism’s love of simple theories gained favor in English philosophy, reveals the stakes with poignant clarity: “though the question of realism and nominalism has its roots in the technicalities of logic, its branches reach about our life.”
EP1 contains the six famous Popular Science Monthly papers, “The Fixation of Belief,” “How to Make Our Ideas Clear,” “The Doctrine of Chances,” “The Probability of Induction,” “The Order of Nature,” and “Deduction, Induction, and Hypothesis.” They form the foundation of Peirce’s pragmatism by providing it with a logically grounded maxim that in time Peirce will often reformulate, notably in exact semiotic terms, for Peirce saw it not as an axiom or postulate but as a provable theorem, and a very fundamental one at that. They also provide that maxim with the context of its application within the logic of scientific inquiry and the conception of an evolutionary universe that accompanies it.
Worth perusing are selections from Peirce’s two papers on the “Algebra of Logic” (1880 and 1885) along with his 1882 remarks on the study of logic. Peirce discusses the relationship between thinking and cerebration (what might be going on in the brain), formulates his logic of the copula using statements of inclusion, considers the kinds of signs required for an adequate logic notation (icons, indexes, and tokens or symbols), and makes the case that logic should form the core of any liberal education.
With “Design and Chance,” “One, Two, Three: Kantian Categories,” and “A Guess at the Riddle,” Peirce generalizes his three categories of 1867 into fundamental elementary but dynamic conceptions capable of providing an account of far more than just the operation of expressing judgments of distinct adicities. They are now extended to nature and the universe, to evolutionary processes, and to every object of scientific inquiry in the human and hard sciences.
Volume 1 ends with the five papers forming the 1891–1892 Monist metaphysical series, in which Peirce applies his evolutionary philosophy to metaphysical questions. Peirce will show that philosophy requires thoroughgoing evolutionism, that mental phenomena fall into three categorial classes, that the fundamental law of mental action is that feelings and ideas will spread, that objective idealism is the only intelligible theory of the universe, and that chance and continuity are indispensable conceptions for framing a philosophical theory compatible with modern science. Peirce attacks determinism as a nominalistic doctrine that fails to capture the logic of natural phenomena, and makes the case for his tychism, which acknowledges the reality of chance as a source of natural variability. He develops his synechism, the doctrine that continuity is the key to any inquiry because it accounts for the continuous spreading of ideas and for their resulting generalization that is central to the law of mind. He takes the occasion to study continuity from the standpoint of mathematics, paying homage to Cantor, and to update insights he had begun to formulate twenty years earlier on the connection between consciousness and time. He pursues his inquiry into physiology with elaborate discussions of the constitution of matter and of protoplasm, whose main physical properties are associated with the main types of mental action, showing especially the role of habit-taking, and how, under the latter aspect, idealism should not fear a mechanical theory of life. In the last text of the volume, “Evolutionary Love,” Peirce develops his agapism, the principle according to which the law of love is operative in the world. Of the three categorially distinct kinds of evolution, the most fundamental is that by creative love, which governs the development of ideas through their sympathetic apprehension and recognition by virtue of the continuity of thought.
“It is not by dealing out cold justice to the circle of my ideas that I can make them grow, but by cherishing and tending them as I would the flowers in my garden.”
Chronology ix
Foreword xi
Introduction by Nathan Houser xix
Contents
1. On a New List of Categories (1867) I
THE JOURNAL OF SPECULATIVE PHILOSOPHY
COGNITION SERIES
2. Questions Concerning Certain Faculties Claimed for Man (1868) II
3. Some Consequences of Four Incapacities (1868) 28
4. Grounds of Validity of the Laws of Logic (1869) 56
5. Fraser's The Works of George Berkeley (1871) 83
6. On a New Class of Observations, suggested by the principles of Logic (1877) 106
ILLUSTRATIONS OF THE LOGIC OF SCIENCE
7. The Fixation of Belief (1877) 109
8. How to Make Our Ideas Clear (1878) 124
9. The Doctrine of Chances (1878) 142
10. The Probability of Induction (1878) 155
11. The Order of Nature (1878) 170
12. Deduction, Induction, and Hypothesis (1878) 186
13. [from] On the Algebra of Logic (1880) 200
14. Introductory Lecture on the Study of Logic (1882) 210
15. Design and Chance (1883-84) 215
16. [from] On the Algebra of Logic: A Contribution to the Philosophy of Notation (1885) 225
17. An American Plato: Review of Royce's Religious Aspect of Philosophy (1885) 229
18. One, Two, Three: Kantian Categories (1886) 242
19. A Guess at the Riddle (1887-88) 245
20. Trichotomic (1888) 280
THE MONIST METAPHYSICAL SERIES
21. The Architecture of Theories (1891) 285
22. The Doctrine of Necessity Examined (1892) 298
23. The Law of Mind (1892) 312
24. Man's Glassy Essence (1892) 334
25. Evolutionary Love (1893) 352
Notes 373
Index 389
Charles Sanders Peirce was born on 10 September 1839 in Cambridge, Massachusetts—when Darwin was only 30 years old—and he lived until 1914, the year World War I began. His father, Benjamin Peirce, was a distinguished professor at Harvard College and the most respected mathematician in America. The Peirce family was well connected in academic and scientific circles, and Charles grew up on intimate terms with the leading figures. He was regarded as a prodigy both in science and philosophy, and more brilliant in mathematics than even his father. Unfortunately for Peirce, his independence of mind, which was at first so much admired, turned out to be a severe impediment to his success. In part this was due to the times. For, as James Feibleman has pointed out, with the expansion of the United States and the rise of the great western cities, New England, and especially Boston and Cambridge, became more and more insular and conservative and grew fearful of genius and originality.(1) As great a thinker as any that America has ever produced, Peirce was thwarted at almost every turn, and only by great effort of will was he able to fulfill some of the promise he exhibited as a young man.
Peirce’s importance as a thinker was not entirely lost on his own age. Among his friends and admirers were such respected philosophers as William James, Josiah Royce, and John Dewey, and the renowned mathematician and logician Ernst Schröder. Yet after a short tenure at the Johns Hopkins University as a part-time lecturer in logic (1879-1884), and a premature—and forced—retirement (1891) from the U. S. Coast and Geodetic Survey where he was in charge of gravity experiments and pendulum research, Peirce was unable to obtain regular employment again. He spent much of the latter third of his life struggling to make ends meet, and many of his writings of those years were done for pay. These include book reviews for newspapers and popular journals, contributions to dictionaries and encyclopedias, and translations (mainly from French and German). There were also a number of philosophical articles composed to satisfy the expectations and instructions of paying editors. For a period, beginning about 1890, Peirce’s life was often dominated by one unsuccessful "get rich" scheme after another. (2) By the turn of the century, he began to worry about getting his program of philosophy and his discoveries in mathematics and logic into print, but almost all his proposals failed to win support. It was more than twenty years after his death, and only after the Harvard Philosophy Department brought out a collection of his papers, that scholars began more generally to glimpse the importance and profundity of his thought. By 1936 Alfred North Whitehead would describe America as the developing center of worthwhile philosophy, and identify Charles Peirce and William James as the founders of the American renaissance. "Of these men," Whitehead said, "W.J. is the analogue to Plato, and C.P. to Aristotle." (3)
Interest in Peirce has grown enormously in recent years, and estimates of his significance as a thinker continue to run high. His work in logic, algebraical and graphical, has come to be regarded as substantial both for its historical impact and its enduring importance for research. Hilary Putnam expressed his surprise upon discovering "how much that is quite familiar in modern logic actually became known to the logical world through the efforts of Peirce and his students," (4) and W. V. Quine dates modern logic from "the emergence of general quantification theory at the hands of Frege and Peirce." (5) More recently, John Sowa has demonstrated how Peirce’s graphical system of logic (his existential graphs) improves on other logics for the representation of discourse, and the study of language generally, and he has used the existential graphs as the logical foundation for his own conceptual graphs, "which combine Peirce’s logic with research on semantic networks in artificial intelligence and computational linguistics." (6) In philosophy more generally, Peirce’s work has been the focus of a considerable resurgence of interest throughout the world. This is demonstrated by the growing number of books and articles about Peirce, by increasing references to his ideas, and by the testimony of respected philosophers like Karl Popper, who regards Peirce as "one of the greatest philosophers of all time." (7) Finally, in the rapidly growing field of study known as semiotics, Peirce is universally acknowledged as one of the founders, even the founder, and his theory of signs is among the most frequently studied and systematically examined of all foundational theories. The importance of semiotics for all disciplines that deal crucially with representation (among them epistemology, linguistics, anthropology, and cognitive science, and probably all the fine arts) is only beginning to be recognized. In his 1989 Jefferson Lecture, Walker Percy argued that modern science is radically incoherentÑ"not when it seeks to understand things and subhuman organisms and the cosmos itself, but when it seeks to understand man, not man's physiology or neurology or his bloodstream, but man qua man, man when he is peculiarly human"—but that, with his theory of signs, Peirce laid the groundwork for a coherent science of man that is yet to be worked out.(8)
Peirce developed an early interest in philosophy, particularly the writings of Kant, and in formal logic, but his training led him to experimental science, especially two sciences with a marked mathematical basis: astronomy and geodesy. His first book, Photometric Researches (1878), was the result of several years of astronomical observations at the Harvard Observatory. It included Ptolemy's catalogue of stars, in a translation Peirce made from a manuscript in the Bibliothèque Nationale in Paris. His published many papers and monographs on geodesy, and one of these is still considered a classic in the field. He was a geodesist with the U.S. Coast and Geodetic Survey for nearly thirty years, and later he worked for a time as a consulting chemical engineer for the St. Lawrence Power Company.
But throughout his life, committed as it was to science, he maintained a continuing research program in philosophy and logic. He delivered series of lectures at different institutions from the mid-1860s until after the turn of the century and, from 1879 to 1884, he taught logic at the Johns Hopkins University, the first true graduate school in America. When in the late 1880s he wrote definitions for the Century Dictionary, it was no doubt his enthusiasm for the Hopkins model that led him to define "university" as "an association of men for the purpose of study, which confers degrees which are acknowledged as valid throughout Christendom, is endowed, and is privileged by the state, in order that the people may receive intellectual guidance and that the theoretical problems which present themselves in the development of civilization may be resolved." The definition was the subject of an anecdote by John Jay Chapman:
Charles Peirce wrote the definition of University in the Century Dictionary. He called it an institution for purposes of study. They wrote to him that their notion had been that a university was an institution for instruction. He wrote back that if they had any such notion they were grievously mistaken, that a university had not and never had had anything to do with instruction and that until we got over this idea we should not have any university in this country. (9)
In his day, Peirce was a more international figure than is generally known. He visited Europe five times between 1870 and 1883, and although he usually traveled as a scientist—to swing pendulums and to compare American weights and measures with European standards—he met prominent mathematicians and logicians as well as scientists, including De Morgan, McColl, Jevons, Clifford, and Herbert Spencer. Peirce corresponded with most of these scholars, and also with Schrõder, Cantor, Kempe, Jourdain, Victoria Lady Welby, and others. Through Lady Welby, Peirce’s letters on semiotic were occasionally passed on to C. K. Ogden who, with I. A. Richards, published some of them in their classic The Meaning of Meaning. Wittgenstein's good friend, F. P. Ramsey, was much impressed with these letters and, in his review of the Tractatus, remarked that Wittgenstein would have profited from Peirce’s type-token distinction. (10)
Peirce’s systematic philosophy, which is the focus of the present collection of writings, is difficult to characterize in a few words. For one thing, it consists of a number of distinct but inter-related theories and doctrines, any one of which could easily be the subject of whole books—as some, in fact, have been. Among the most characteristic of Peirce’s theories are his pragmatism (or "pragmaticism," as he later called it), a method of sorting out conceptual confusions by relating meaning to consequences; semiotic, his theory of information, representation, communication, and the growth of knowledge; objective idealism, his monistic thesis that matter is effete mind (with the corollary that mind is inexplicable in terms of mechanics); fallibilism, the thesis that no inquirer can ever claim with full assurance to have reached the truth, for new evidence or information may arise that will reverberate throughout one's system of beliefs affecting even those most entrenched; tychism, the thesis that chance is really operative in the universe; synechism, the theory that continuity prevails and that the presumption of continuity is of enormous methodological importance for philosophy; and, finally, agapism, the thesis that love, or sympathy, has real influence in the world and, in fact, is "the great evolutionary agency of the universe." The last three doctrines are part of Peirce’s comprehensive evolutionary cosmology.
Besides this imposing assemblage of theories, there is still another barrier to an easy characterization of Peirce’s philosophy, signalled by the reference to Darwin in the opening paragraph. Peirce’s philosophy does not consist of a set of static doctrines, thought up and written down once and for all; its development over his more than fifty years of scholarship appropriately represents his Darwinian motivation. Not only did he think of himself as working out an evolutionary philosophy, one that includes humankind as part of the evolving natural world, but his writings illustrate his personal commitment to the principle of evolutionary growth. Peirce was always open to the revelations of experience and was prepared to change his theories accordingly. Some of these changed dramatically over the course of his life; nearly all changed in one way or another. We cannot draw one consistent philosophy from Peirce’s writings without ignoring conflicting passages. A tendency by some of Peirce’s commentators to overlook this characteristic of his thought has led to much confusion. This point was made rather dramatically by the late Indiana philosopher, Arthur F. Bentley:
What one says 20 years from what one says another time, must be studied as Event-in-process....Peirce did not have a modernized post-Jamesian vocabulary for behaviors. He floundered and turned....you can show Peirce as all sorts of things. But take the full flow of Peirce’s development, his 1869 essays for actuality; his relations logic—his statement about concepts in 187[8] Sci Monthly; his late effort at a functional logic nobody ever mentions, etc. You have an event in progress. It is, for me, one of the greatest event[s] among all events. (11)
It is impossible, in a short introduction, to present fully Peirce’s most characteristic philosophical doctrines and theories, let alone give serious attention to the development of his thought. It is difficult to give even a satisfactory outline of his philosophical development. Over the years, scholars have described the key steps in his intellectual life in different ways. To give some chronological structure to such studies, Max Fisch has divided Peirce’s philosophical activity into three periods. (1) The Cambridge period (1851-1870), from his reading of Whately's Logic to his memoir on the logic of relatives; (2) the cosmopolitan period (1870-1887), the time of his most important scientific.work, when he traveled extensively in Europe, as well as in the United States and Canada; and (3) the Arisbe period (1887-1914), from his move to Milford, Pennsylvania, until his death—the longest and philosophically most productive period. (12)
Gérard Deledalle has associated these periods more directly with Peirce’s philosophical activity and has given them more figurative names. (1) "Leaving the Cave" (1851-1870), the period of the evolution of Peirce’s thought beginning with his critique of Kantian logic and Cartesianism; (2) "The Eclipse of the Sun" (1870-1887), the period dominated by his discovery of modern logic and pragmatism; and (3) "The Sun Set Free" (1887-1914), the period of his founding of semiotic on a phenomenology based on his logic of relations and of his working out his scientific metaphysics, the crowning-point of his philosophical achievement. (13)
A somewhat different account of the principal stages of Peirce’s development is given by Murray Murphey, who associates each of Peirce’s key shifts of thought with important discoveries in logic. He identifies four main phases: (1) Peirce’s Kantian phase (1857-1865/66); (2) the phase beginning with the discovery of the irreducibility of the three syllogistic figures (1866-1869/70); (3) the phase beginning with the discovery of the logic of relations (1869/70-1884); and (4) the phase beginning with the discovery of quantification and of set theory (1884-1914). (14)
Probably the most significant development in Peirce’s intellectual life was the evolution of his thought from its quasi-nominalist and idealist beginnings to its broadly and strongly realist conclusion. Because there are so many variants of these doctrines, a few selections from Peirce’s Century Dictionary definitions will help reveal his conceptions of these terms:
Nominalism: 1. The doctrine that nothing is general but names; more specifically, the doctrine that common nouns, as man, horse, represent in their generality nothing in the real things, but are mere conveniences for speaking of many things at once, or at most necessities of human thought; individualism.
Idealism: 1. The metaphysical doctrine that the real is of the nature of thought; the doctrine that all reality is in its nature psychical.
Realist: 1. A logician who holds that the essences of natural classes have some mode of being in the real things; in this sense distinguished as a scholastic realist; opposed to nominalist. 2. A philosopher who believes in the real existence of the external world as independent of all thought about it, or, at least, of the thought of any individual or any number of individuals.
Peirce also defined "ideal-realism" as "a metaphysical doctrine which combines the principles of idealism and realism." As a variant of this term, he defined the ideal-realism of his father as "the opinion that nature and the mind have such a community as to impart to our guesses a tendency toward the truth, while at the same time they require the confirmation of empirical science."
The life-long tension between nominalism and realism in Peirce’s own intellectual life is testament to the general importance he attached to it; in fact, if any single question can be said to have been viewed by Peirce as the most important philosophical question of his time, it is that of deciding between the two doctrines. Peirce concurred in this with his old schoolmate Francis Ellingwood Abbot, who in 1885 wrote that "so far was the old battle of Nominalism and Realism from being fought out by the end of the fifteenth century that it is to-day the deep, underlying problem of problems, on the right solution of which depends the life of philosophy itself in the ages to come." (15) For Peirce, as for Abott, the significance of the outcome of this "battle" was not limited to technical philosophy:
though the question of realism and nominalism has its roots in the technicalities of logic, its branches reach about our life. The question whether the genus homo has any existence except as individuals, is the question whether there is anything of any more dignity, worth, and importance than individual happiness, individual aspirations, and individual life. Whether men really have anything in common, so that the community is to be considered as an end in itself, and if so, what the relative value of the two factors is, is the most fundamental practical question in regard to every institution the constitution of which we have it in our power to influence. (item 5)
According to Fisch, Peirce’s progress toward realism began early and was gradual, but there were key steps that divide it into stages. (16) Peirce took his first deliberate step in 1868 when, in the second paper of his cognition series (item 3), he "declares unobtrusively for realism." Although this step marks only a small shift in Peirce’s thought—the introduction of "the long run" into his theory of reality—it is an important one, for it brings to an end his period of avowed nominalism. (17)
Peirce’s second deliberate step was taken in 1871, when in his Berkeley review (item 5) he again declared for "the realism of Scotus" and recognized that realism is temporally oriented toward the future while nominalism is oriented toward the past. Fisch points out that this second declaration came, when after a period of intensive study of the schoolmen, Peirce had become well acquainted with the writings of Duns Scotus.
Peirce took his third step in mid-1872 when, in the Cambridge Metaphysical Club, he first presented his pragmatism in which the meaning of conceptions is referred to future experience: "So we say that the inkstand upon the table is heavy. And what do we mean by that? We only mean that if its support be removed it will fall to the ground.... So that ... knowledge of the thing which exists all the time, exists only by virtue of the fact that when a certain occasion arises a certain idea will come into the mind" (W3:30-31). A few months later, Peirce wrote that "no cognition ... has an intellectual significance for what it is in itself, but only for what it is in its effects upon other thoughts. And the existence of a cognition is not something actual, but consists in the fact that under certain circumstances some other cognition will arise" (W3:77). But the best known statement of the doctrine came in 1878, in the second of his "Illustrations of the Logic of Science," in the now famous version of his pragmatic maxim: "consider what effects, which might conceivably have practical bearings, we conceive the object of our conception to have. Then, our conception of these effects is the whole of our conception of the object." Fisch stops enumerating the steps toward realism in 1872, and divides the rest of Peirce’s development into two periods, the pre-Monist period (1872-1890) and the Monist period (1891-1914). He summarizes the key factors of the former period as follows:
The chief developments in the pre-Monist period whose effects on Peirce’s realism will appear in the Monist period are his pragmatism; his work on the logic of relations and on truth-tables, indices, and quantification; the resulting reformulation of his categories; his work and that of Cantor and Dedekind on transfinite numbers; the appearance in 1885 of provocative books by Royce and Abbot; and, at the end of the period, a fresh review of the history of philosophy for purposes of defining philosophical terms for the Century Dictionary.
In the pre-Monist period, a step that had special importance for Peirce’s philosophical development was his recognition, with the help of his Johns Hopkins student O. H. Mitchell, of the need for indices in his algebra of logic. Peirce recognized the need for indices in notations adequate for the full representation of reasoning because he had come to understand the importance of pinning down thought to actual situations. "The actual world," he said, "cannot be distinguished from a world of imagination by any description. Hence the need of pronouns and indices" (item 16). Fisch points out that Peirce’s incorporation of indices into his system of logic called for a reformulation both of his theory of signs and of his general theory of categories. It was then that Peirce reintroduced the familiar icon-index-symbol trichotomy and his reformulated categories denoting three kinds of characters (singular, dual, and plural), which he associated with three kinds of fact: "fact about an object, fact about two objects (relation), fact about several objects (synthetic fact)" (W5:244).
At the end of the pre-Monist period, Peirce took a major step toward a more robust realism, a step related to his recognition of the need for indices. This was his acceptance, in about 1890, of Scotus's haecceities—the reality of actuality or of secondness. Peirce could no longer ignore the "Outward Clash," as Hegel had much to the detriment of his system of philosophy. With the acceptance of the reality of seconds, Peirce acknowledged the mode of being that distinguishes the individual from the general, and isolated his categories of fact: qualia, relations, and signs.
The Monist period began with the series of five papers that concludes the present volume. It is the first of four series of papers that Peirce contributed to the Monist which, after its founding in 1890, became his chief medium of publication. In each of these series, and in many of his other writings of the period, he continued to weed out the remaining nominalistic and many of the idealistic elements of his philosophy. Peirce took his most decisive step toward realism in 1897. Fisch has nicely illustrated this last great step by contrasting two passages, one from a January 1897 review of the third volume of Schr&3246der's Algebra und Logik der Relative, and the other from an 18 March 1897 letter to William James. In January, Peirce wrote: "I formerly [as late as October 1896] defined the possible as that which in a given state of information (real or feigned) we do not know not to be true. But this definition today seems to me only a twisted phrase which, by means of two negatives, conceals an anacoluthon" (CP 3.527). Two months later he wrote to James: "The possible is a positive universe, and the two negations happen to fit it, but that is all" (CP 8.308). Peirce thus added the possible as a third mode of being—and, in so doing, gave up his long-held, Mill-inspired frequency theory of probability—and his scheme of categories was fundamentally complete. To his categories in their form of thirdness (feeling, or signs of firstness; sense of action and reaction, or signs of secondness; and sense of learning or mediation, or signs of thirdness) and in their form of secondness (qualia, or facts of firstness; relations, or facts of secondness; and signs, or facts of thirdness), Peirce now added what might be called his ontological categories, his categories in their form of firstness: firstness, or the being of positive qualitative possibility; secondness, or the being of actual fact; and thirdness, or the being of law that will govern facts in the future (CP 1.23).
Peirce was then, in 1897, what Fisch calls a "three-category realist." He had very early accepted the reality of thirds, the universe of thought or signs. This universe was the only reality Peirce the idealist had admitted until about 1890 when he accepted the reality of seconds, the universe of facts (influenced by Scotus). Finally, in 1897 he broadened his evolving realism to accept the reality of firsts, the universe of possibility (influenced by Aristotle). Recognizing the significance of these steps for the growth of his thought, Peirce now characterized himself as "an Aristotelian of the scholastic wing, approaching Scotism, but going much further in the direction of scholastic realism" (CP 5.77n1).
One further step from the Monist period should be mentioned, for it brings together two fundamental strands of Peirce’s thought: his pragmatism and his semiotic. In his third Monist series, beginning in 1905, Peirce sought to prove his doctrine of pragmatism (pragmaticism), and in the course of working out his proof, he wove his two great theories into a unified doctrine. He concluded that his semiotic pragmatism entails realism, so that a proof of pragmatism is, at the same time, a proof of realism, and that the pragmatist is "obliged to subscribe to the doctrine of a real Modality, including real Necessity and real Possibility" (CP 5.457).
Although Peirce was aware that at least some of the steps described above were important milestones in his development, he did not regard them as ushering in new systems of thought. According to Murphey, Peirce regarded each phase of his thought as merely a revision of "a single over-all architectonic system" and always preserved as much as he could from each earlier phase. His philosophy might be likened to "a house which is being continually rebuilt from within." (18)
Some scholars have not accepted the one-system account of Peirce’s philosophy. Thomas Goudge, in particular, has argued that "Peirce’s ideas fall naturally into two broad groups whose opposite character is a reflection of a deep conflict in his thinking" and that this opposition is the result of his conflicting commitment to both naturalism and transcendentalism. (19) By "naturalism" Goudge has in mind scientific philosophy more or less in the positivist sense, a philosophy that puts logical analysis on a pedestal and eschews speculation and system-building. Transcendentalism, on the other hand, discounts logical analysis in favor of metaphysical construction, embracing both speculation and architectonic. Peirce the naturalist tended to nominalism, while Peirce the transcendentalist tended to realism. It was Peirce the naturalist who was the pragmatist, while Peirce the transcendentalist tended to intuitionism. Goudge finds that Peirce’s naturalism was the stronger tendency, which guided him in his researches in formal logic, semiotic, scientific method, phenomenology, and critical metaphysics, while the weaker transcendentalism "is most apparent in his views on cosmology, ethics, and theology." (20)
Goudge has indeed uncovered what may appear to be two Peirces, but the finding of most recent scholarship is that the tension is not as great as he thought. Peirce’s philosophy is broad and subtle and appears to be able to accommodate results that would be incompatible in narrower systems of thought. It is not possible here to argue for the coherence of the various claims and doctrines that Goudge and others have found to be in conflict. The best that can be done is to outline the basic architecture of Peirce’s philosophy and to give a glimpse of its overall unity.
For Peirce, as for Kant, logic was the key to philosophy. He claimed that from the age of twelve, after reading his brother's copy of Whately's Elements of Logic, he could no longer think of anything except as an exercise in logic. (21) Peirce’s study of logic was not limited to the formal theory of deductive reasoning or to the foundations of mathematics, although he made important contributions to both. When he sought the professorship of physics at the Johns Hopkins (before being appointed part-time lecturer in logic), he wrote to President Daniel C. Gilman that it was as a logician that he sought to head that department and that he had learned physics in his study of logic. "The data for the generalizations of logic are the special methods of the different sciences," he pointed out, and "to penetrate these methods the logician has to study various sciences rather profoundly."
But it was not just as a theory of reasoning or as a critique of methods that logic was important for philosophy. "Philosophy," Peirce said, "seeks to explain the universe at large, and to show what there is intelligible or reasonable in it. It is therefore committed to the notion (a postulate, which however may not be completely true) that the process of nature and the process of thought are alike" (NEM 4:375). Whether completely true or not, if philosophy seeks to explain the universe at large, and if our explanations presuppose a rational organization of the universe—which, otherwise, would hardly be explicable at all—then we are, in effect, committed to the thesis that the process of nature is (or is like) a rational process. Logic, therefore, has more than heuristic value for philosophy.
It is important to bear in mind that when Peirce called himself a logician—the first and perhaps only person to have his occupation listed as "logician" in Who's Who—he was not thinking of himself as a logical technician or as a logicist who views logic as the deductive foundation for mathematics. Although his many contributions to technical logic—including his 1881 axiomatization of the natural numbers, his 1885 quantification theory and introduction of truth-functional analysis, and his life-long development of the logic of relations—have considerable importance for the foundations of mathematics, his main concern was to build an adequate theory of science and an objective theory of rationality. His general conception of logic was closer to modern-day philosophy of science, together with epistemology and philosophical logic, than to today's mathematical logic. In his later years, Peirce gave a great deal of attention to the classification and relations of the sciences and he came to associate much of what we would today call mathematical logic with mathematics; logic, on the other hand, he came to regard as a normative science concerned with intellectual goodness and, in his most developed view, it is coextensive with semiotic, which constitutes the very heart of philosophy.
Peirce’s philosophy is thoroughly systematic—some might say it is systematic to a fault. Central to his system is the idea that certain conceptions are fundamental to others, those to still others, and so on; so that it is possible to analyze our various theoretical systems (our sciences) into a dependency hierarchy. At the top of this hierarchy (or at the base if we envision a ladder of conceptions) we find a set of universal categories, an idea Peirce shared with many of the greatest systematic thinkers including Aristotle, Kant, and Hegel. Peirce’s universal categories are three: firstness, secondness, and thirdness. Firstness is that which is as it is independently of anything else. Secondness is that which is as it is relative to something else. Thirdness is that which is as it is as mediate between two others. In Peirce’s opinion, all conceptions at the most fundamental level can be reduced to these three.
This theory of categories, in its most abstracted form, belongs to mathematics, which stands at the pinnacle of the sciences. Peirce followed his father in defining mathematics as the science which deduces consequences from hypotheses—from what is given—but there is more to it than that. Mathematics is a science of discovery that investigates the realm of abstract forms, the realm of ideal objects (entia rationis). It is the mathematician who first discovers the fundamentality of triadicity by finding that monadic, dyadic, and triadic relations are irreducible, while relations of any degree (or adicity) greater than triadic can be expressed in combinations of triadic relations. This is known as Peirce’s reduction thesis.
Mathematics presupposes no other science but is presupposed by all other sciences. After mathematics comes philosophy, which has three main branches: phenomenology, normative science, and metaphysics—dependent on each other in reverse order. Not surprisingly, Peirce’s categories make their appearance in each of these parts of philosophy (as they must if they are universal categories). He explained this in the fifth of a series of lectures on pragmatism given at Harvard in 1903:
Philosophy has three grand divisions. The first is Phenomenology, which simply contemplates the Universal Phenomenon and discerns its ubiquitous elements, Firstness, Secondness, and Thirdness, together perhaps with other series of categories. The second grand division is Normative Science, which investigates the universal and necessary laws of the relation of Phenomena to Ends, that is, perhaps, to Truth, Right, and Beauty. The third grand division is Metaphysics, which endeavors to comprehend the Reality of the Phenomena. (CP 5.121)
Before giving this division, Peirce had warned his audience: "Now I am going to make a series of assertions which will sound wild" (CP 5.120), but he stressed that it was essential to his case for pragmatism.
The three divisions of philosophy are directly related to the categories. In attending to the universal elements of phenomena in their immediate phenomenal character, phenomenology treats of phenomena as firsts. Here the categories appear as fundamental categories of experience (or consciousness): firstness is the monadic element of experience usually identified with feeling, secondness is the dyadic element identified with the sense of action and reaction, and thirdness is the triadic element identified with the sense of learning or mediation as in thought or semiosis.
In attending to the laws of the relation of phenomena to ends, normative science treats of phenomena as seconds. The three normative sciences—esthetics, ethics, logic—were associated with three kinds of goodness: esthetical goodness (esthetics considers "those things whose ends are to embody qualities of feeling"), ethical goodness (ethics considers "those things whose ends lie in action"), and logical goodness (logic considers "those things whose end is to represent something"). The normative sciences correspond to the three categories and are dependent on each other, again in reverse order. Logic (or semiotic), in turn, has three branches: speculative grammar, critic, and speculative rhetoric. (Sometimes Peirce used different names.) Speculative grammar studies what is requisite for representation of any kind; it is the study of the "general conditions of signs being signs" (CP 1.444). Critic is the formal science of the truth of representations; it is the study of the reference of signs to their objects. Speculative rhetoric studies how knowledge is transmitted; it might be called the science of interpretation. (These three branches correspond more or less to Carnap's syntactics-semantics-pragmatics triad, which he learned from Charles Morris who had probably derived it from Peirce.)
The three normative sciences are followed by metaphysics, the third and last branch of philosophy. The general task of metaphysics is "to study the most general features of reality and real objects" (item 21). In attempting to comprehend the reality of phenomena, that is, in treating of phenomena as representing something that is inherently mind-independent, metaphysics treats of phenomena as thirds. Logic (semiotic), the normative science immediately preceding metaphysics, gives structure to metaphysical investigations which are, not surprisingly, replete with triadic divisions. Among these we find possibility, actuality, destiny; chance, law, habit; and mind, matter, evolution.
Most typical of Peirce’s metaphysical theories are his objective idealism and his evolutionary cosmology. In "The Architecture of Theories" (item 21), Peirce characterized objective idealism as holding that "matter is effete mind," mind that has become hide-bound with habit. According to this doctrine, matter is mind that has lost so much of the element of spontaneity through the acquisition of habits that it has taken on the dependable law-governed nature we attribute to material substance. It is the one intelligible theory of the universe, according to Peirce, a monism (or, as he calls it, neutralism) that regards psychical law as primordial, and physical law as derived and special.
Peirce’s wide-ranging evolutionary cosmology is more difficult to characterize briefly. Some regard it as the weakest part of his work; W. B. Gallie called it the "white elephant" of Peirce’s philosophy. (22) But others hail Peirce’s cosmology as the prelude to contemporary cosmological physics. (23) It should be remembered that, according to Peirce, part of the purpose of philosophy is to explain the universe at large. In this he was a follower of the earliest Greek philosophers. In any case, Peirce’s cosmological story goes roughly as follows. (24)
In the beginning there was nothing. But this primordial nothing was not the nothingness of a void or empty space, it was a no-thing-ness, the nothingness characteristic of the absence of any determination. Peirce described this state as "completely undetermined and dimensionless potentiality," which may be characterized by freedom, chance, and spontaneity (CP 6.193, 200).
The first step in the evolution of the world is the transition from undetermined and dimensionless potentiality to determined potentiality. The agency in this transition is chance or pure spontaneity. This new state is a Platonic world, a world of pure firsts, a world of qualities that are mere eternal possibilities. We have moved, Peirce says, from a state of absolute nothingness to a state of chaos.
Up to this point in the evolution of the world, all we have is real possibility, firstness; nothing is actual yet—there is no secondness. Somehow, the possibility or potentiality of the chaos is self-actualizing, and the second great step in the evolution of the world is that in which the world of actuality emerges from the Platonic world of qualities. The world of secondness is a world of events, or facts, whose being consists in the mutual interaction of actualized qualities. But this world does not yet involve thirdness, or law.
The transition to a world of thirdness, the third great step in cosmic evolution, is the result of a habit-taking tendency inherent in the world of events. Peirce liked to illustrate with dice or playing cards how single random events, if their mere occurrence established a tendency, however slight, for the reoccurrence of events of that type, could lead to large scale uniformities. A habit-taking tendency is a generalizing tendency, and the emergence of all uniformities, from time and space to physical matter and even the laws of nature, can be explained as the result of the universe's tendency to take habits. Peirce regarded this surrender of chance and freedom to habit and law as a growth toward concrete reasonableness. Although he at times envisioned an end of history marked by the crystallization of mind that has become completely law-governed and without any residual spontaneity (truly concrete reasonableness), he sometimes held that an element of freedom and originality will persist in a universe that has reached a state of equilibrium between chance and law.
This is only a partial sketch of some of the characteristic theories and doctrines of Peirce’s metaphysics, the third and final division of philosophy. It does not account for the role of semiosis or the power of love in the evolution of the cosmos, nor does it distinguish between the different modes of evolution that characterize Peirce’s more developed thought (as in item 25). (In his classification of the sciences, philosophy is followed by the special sciences, such as physics and psychology, then by sciences of review, and, finally, by practical sciences like pedagogics.)
The preceding summary provides a mere skeletal account of Peirce’s system of philosophy, but it should suffice to convey a sense of both its breadth and unity. When viewed as a whole, Peirce’s philosophy may be characterized in different ways but, however characterized, it must be said to be a scientific philosophy. This acknowledges both its empirical character and its adherence to scientific, or experimental, methodology. Certainly it is appropriate to call Peirce’s philosophy an empirical philosophy, and he himself thought of his pragmatism as a prope-positivism. But Peirce should probably not be regarded, as he sometimes is, as a positivist.
Peirce asserted quite emphatically that "experience is our only teacher," and thus embraced a fundamental tenet of classical empiricism. Yet he rejected the doctrine of a tabula rasa, claiming that there "is not one drop of principle in the whole vast reservoir of established scientific theory that has sprung from any other source than the power of the human mind to originate ideas that are true." But this power to originate ideas is feeble, Peirce said, and "the truths are almost drowned in a flood of false notions." Experience enables us to "filter off" the false ideas, "letting the truth pour on in its mighty current" (CP 5.50).
Peirce’s devotion to mathematics and science, his emphasis on the scientific method, and his pragmatic maxim (which sounds a lot like a verification principle) certainly suggest an affinity between pragmatism and positivism. As late as 1905, he explained the purpose of his pragmatism in a way that seems to share significant positivist concerns:
It will serve to show that almost every proposition of ontological metaphysics is either meaningless gibberish—one word being defined by other words, and they by still others, without any real conception ever being reached—or else is downright absurd; so that all such rubbish being swept away, what will remain of philosophy will be series of problems capable of investigation by the observational methods of the true sciences. (CP 5.423)
The pragmatic maxim may thus be taken as a test for whether our conceptions, and our theories, are indexed to experience, or whether they are part of a mere language game. But though there are many points in common between pragmatism and positivism, there are important differences, especially Peirce’s insistence on realism and on the legitimacy of abductive reasoning, and his denial of a sharp demarcation between the language of observation and the language of theory. (25)
Peirce’s general philosophy is sometimes called a pragmatic philosophy, where pragmatism is taken as more than just a theory of meaning or a method for analyzing conceptions. It combines Peirce’s brand of empiricism with scientific method and the process orientation of Darwin's evolutionism—together with an Aristotelian teleological twist—into a broad philosophical program. It is a philosophy in which purpose appears to play the part for Peirce that intentionality played for Brentano. The mark of intelligence, on Peirce’s view, is purpose, and purpose is always related to action. Peirce’s pragmatism may thus be seen as a praxis philosophy: "The elements of every concept enter into logical thought at the gate of perception and make their exit at the gate of purposive action; and whatever cannot show its passports at both those two gates is to be arrested as unauthorized by reason" (CP 5.212).
Pragmatism, however, focuses on intellectual purport, which would seem to encompass only part of the range of possible semiosis. Consequently, pragmatism may be narrower than, or apply to only part of, Peirce’s general theory of signs. Perhaps it is best to describe his philosophy as a semiotic philosophy. But is it a semiotic idealism or realism? As either alternative can be supported, the choice seems to depend on who makes it.
According to David Savan, Peirce is a semiotic idealist. Savan distinguishes between two forms of semiotic idealism: a mild variety that holds that any properties, attributes, or characteristics of whatever exists depend upon the system of signs, representations, or interpretations through which they are signified, and a strong variety that holds that the very existence of anything depends upon the system of signs, representations, and interpretations which purport to refer to it. Savan claims that Peirce is a mild semiotic idealist. (26)
According to Thomas Short, on the other hand, Peirce is a semiotic realist. (27) The decision to label Peirce one way or the other seems to reflect the relative importance one attaches to the different elements of the sign relation, and often seems to be a matter of emphasis rather than a divergence of doctrine. Since he explicitly embraced a more and more encompassing realism, it might seem more appropriate to follow Short and call Peirce a semiotic realist—especially as that reflects his pragmatic admonition that our conceptions are meaningless unless they have reference to something outside of intellect: "it is necessary that a method should be found by which our beliefs may be determined by nothing human, but by some external permanency—by something upon which our thinking has no effect" (item 7). Yet one could counter that Peirce’s adherence to his doctrine of objective idealism also recommends Savan's viewpoint. It is interesting to consider whether Peirce’s philosophy might be best represented in his definition of his father's ideal-realism, which "combines the principles of idealism and realism."
Peirce’s theory of signs has, more than any of his other theories, attracted wide-spread attention in recent years. It was an outgrowth of many factors and influences including, perhaps primarily, his study of and reaction to Schiller but especially Kant; his study of logic, most importantly the logics of De Morgan and Boole (and also those of Aristotle and the medieval logicians); his reaction to Darwin and the idea of evolution; and, finally, the growing abstraction in mathematics, perhaps especially the development of topology and non-Euclidean geometry. Under all these influences Peirce acquired new insights and directions, and was led along paths never before traveled. But, more than anything else, it was his discovery that his sign conception could clear up many hitherto intractable philosophical problems that convinced him of the importance of signs. After rejecting certain Kantian restrictions on what could or could not be represented, he undertook an investigation of the entire range of representability and studied, among other things, conceptions of God, mathematical infinity, totality, immediacy, and necessity. As a result of these investigations Peirce developed and sharpened his semiotic ideas, and with the addition of certain phenomenological conceptions (perhaps from Schiller), he arrived at the view that "all consciousness is sign consciousness" and that in studying signs one addresses "whatever could be a subject of philosophic concern and insight." (28) Believing that in semiotic he had a better ground for philosophy than in traditional epistemology, Peirce worked at expanding his findings into a general theory of signs, and later, in considering what the universe must be like for signs (or semiosis) to be possible, he built a semiotic framework for most of his major philosophical work.
In its most abbreviated form, Peirce’s theory of signs goes something like this. A sign is anything which stands for something to something. What the sign stands for is its object, what it stands to is the interpretant. The sign relation is fundamentally triadic: eliminate either the object or the interpretant and you annihilate the sign. This was the key insight of Peirce’s semiotic, and one that distinguishes it from most theories of representation that attempt to make sense of signs (representations) that are related only to objects.
As his theory evolved, Peirce came to distinguish between different kinds of objects and interpretants. Every sign has two objects, a dynamic object, "the really efficient but not immediately present object," and an immediate object, "the object as the sign represents it." And every sign has three interpretants, a final (or logical) interpretant, which is the "effect that would be produced on the mind by the sign after sufficient development of thought," a dynamic interpretant, which is the "effect actually produced on the mind," and an immediate interpretant, which is the "interpretant represented or signified in the sign" (CP 8.343). Any given sign only partially reveals its dynamic object, and that partial revelation constitutes its immediate object. Similarly, the final interpretant of a sign is the result of (or is what would result from) a history of semiotic interaction with the given dynamic object, while the dynamic interpretant is the effect the sign actually produces (at a given time), and the immediate interpretant is the immediate significance of the sign independent of any previous history involving its object.
Peirce explained that signs can be divided in different ways according to this analysis of the structure of signs. If we consider the nature of any given sign (the ground of the sign), it will be found to be intrinsically either a quality (a qualisign), existent thing or event (a sinsign), or a law or habit (a legisign). If we consider a sign's relation to its dynamic object, we will find that it is like its object (an icon), that it has an actual, existential connection with its object (an index), or that it is related to its object by convention or habit (a symbol). If we consider the relation of the sign to its final interpretant—how the sign is interpreted—it will appear to be a sign of possibility (a rheme), a sign of actual existence (a dicent), or a sign of law (an argument). Since every sign is something in itself, has a relation to its object, and represents its object in some way or other, the above divisions can be used to yield a classification of signs that makes more distinctions than most rival theories.
Using only these three triadic divisions of signs, as Peirce often did, we derive a ten-fold classification of signs sufficient for most analytical purposes. For example, we can identify a paint chip (as a sign of color) as a rhematic-iconic-qualisign, a weathervane as a dicent-indexical-sinsign, and a proper name as a rhematic-indexical-legisign. But, unfortunately, as anyone knows who has tried to work out examples of Peirce’s classes, it is not as easy as we might think—which either means that we do not quite understand Peirce or that his theory is a bit ambiguous.
The fact is, Peirce did not settle exclusively on his ten-fold classification of signs, but developed a more complex classification based on ten rather than three triadic divisions. In this fuller analysis Peirce considered such three-fold divisions as the nature of immediate objects (descriptives, or indefinites; designatives, or singulars; and copulatives, or generals) and the nature of the assurance afforded the interpreter (abducents, or assurance by instinct; inducents, or assurance by experience; and deducents, or assurance by form or habit). With these ten divisions, Peirce was able to isolate sixty-six distinct classes of signs and, thus, to eliminate most of the ambiguity of his more abbreviated classification. But Peirce never completed this part of his general theory, and the precise nature and order of the ten trichotomies remains an important problem for semiotic theorists to work out more fully. Perhaps in our present state of understanding of language and semiosis we have no need for such complexity—just as we once had no need for relativity physics—but where principled distinctions can be made, they will probably someday be needed.
So far, this sketch of Peirce’s theory of signs has focussed on speculative grammar, which considers "in what sense and how there can be any true proposition and false proposition, and what are the general conditions to which thought or signs of any kind must conform in order to assert anything" (CP 2.206). The philosopher who concentrates on this branch of semiotic investigates representation relations (signs), seeks to work out the necessary and sufficient conditions for representing, and classifies the different possible kinds of representation. Speculative grammar is often presented as if it were the whole of Peirce’s semiotic, perhaps because that is where we encounter some of his best-known trichotomies.
The second branch of semiotic, critic, is "the science of the necessary conditions of the attainment of truth" (CP 1.445). It is "that part of logic ... which, setting out with such assumptions as that every assertion is either true or false, and not both, and that some propositions may be recognized to be true, studies the constituent parts of arguments and produces a classification of arguments" (CP 2.205). By means of this classification, arguments "that are bad are thrown into one division, and those which are good into another, these divisions being defined by marks recognizable even if it be not known whether the arguments are good or bad." To complete its task, critic "has to divide good arguments by recognizable marks into those which have different orders of validity, and has to afford means for measuring the strength of arguments" (CP 2.203). Thus, in addition to investigating truth conditions in general, the philosopher who concentrates on critic will investigate Peirce’s well-known division of reasoning into abduction, induction, and deduction (and the corresponding theories of abductive, inductive, and deductive logic). Much of what made up the traditional logic curriculum belongs in critic, as does much that is dealt with in philosophical logic, especially topics that concern truth and reference.
The third branch of semiotic, speculative rhetoric, is "the study of the necessary conditions of the transmission of meaning by signs from mind to mind, and from one state of mind to another" (CP 1.445). More succinctly, it studies the conditions for the development and growth of thought. The focus for the philosopher who studies this branch is the relation between representations and interpreting thoughts (or interpretations). Whereas critic is the science of the necessary conditions for the attainment of truth, speculative rhetoric is the science of the general conditions for the attainment of truth. Peirce often emphasized the study of methods of reasoning as a main concern of speculative rhetoric, and he sometimes suggested that this branch of logic might be better named "methodeutic." Questions of meaning and interpretation dominate this branch, and it may be that pragmatism, as a theory of meaning or inquiry, belongs here. So may the contemporary study of hermeneutics, something Peirce himself once suggested, although with reference to Aristotle's hermeneutic. Be that as it may, it would appear that Peirce’s theory of signs encompasses much of what lies at the heart of modern philosophy, and it has significance for many other disciplines.
Peirce’s analysis of the sign relation as fundamentally triadic motivated much that is unique in his philosophy. His insistence that every interpretant is related to its object through the mediation of a sign constitutes a denial of intuition; for intuition requires a direct dyadic relation between an interpretant and its object—somehow we just know something about an object (a person, a state of affairs, whatever) without the intervention of a sign. There is no good reason to suppose that we have such a faculty, as Peirce argued in the first paper of his cognition series (item 2). (And yet, in a different sense, Peirce gives us a compelling theory of intuition. With an appeal to abduction and to his belief that we are attuned to nature through centuries of evolutionary development—so that we are actual embodiments of natural principles—Peirce argues, following his father, that we have a natural inclination to the truth, a tendency to guess correctly. But this is a semiotic kind of intuition that bears the Peircean sign of the three.)
But how does an object determine its interpretant through the mediation of a sign? According to Peirce, the dynamic object, the really efficient but not immediately present object, is the object that somehow determines the sign and through the sign mediately determines an interpretant. How can an object that is external to the sign (the immediate object is the internal object) be a determining force in shaping the interpretant? Notice that this amounts to asking how objects (or the external world) can determine mind.
Every sign represents an object (in some way or other) to the interpretant. The interpretant is, or helps make up, a habit that "guides" our future (and present) actions, or thought with respect to the object in question, or objects like the one in question. If the interpretant is untrue to the object, our behavior will not be (or may not be) successful—reality will have its way with us. Not until our interpretants (our ideas or intellectual habits) are fully attuned to their objects will we avoid unexpected confrontations with a resistant reality. In this way, the real object determines or shapes our mind, our reservoir of intellectual habits.
Does this make Peirce a semiotic realist? It would seem so. Not only does the mind represent the world, it represents it in a certain way: namely, the way it is forced to represent the world by the resistance of the world to error. Surely this is a kind of realism. And it is also a semiotic account of pragmatism which, as Christopher Hookway points out, "is supposed to explain how an independent reality can constrain our opinions through perception." (29)
But this is not the whole story. There are many ways to live in the world, and intellect does not constrain us to a single path. There is far more to an intellect than the mere representation of external objects: there are plans and purposes and ideals, all of which can be infixed in intellectual habits that predetermine future behavior. And, of course, future behavior will shape the world that is to come. What is so interesting about Peirce’s views is that we as individuals, we as humanity, have some measure of control over our intellectual habits. We have a choice. We can deliberately, though with effort, change our intellectual habits—which means that we can change our minds: and that means that we have some measure of control over which of the many possible futures will be ours. Perhaps this is semiotic idealism but, if so, it is an idealism compatible with semiotic realism.
Peirce’s inclusion of the interpretant as fundamental in the sign relation shows that all thought is to some degree a matter of interpretation. All advanced thought uses symbols of one kind or another, and thus rests on convention. On Peirce’s view, then, all advanced thinking depends on one's participation in a linguistic or semiotic community. Peirce’s stress on the importance of community was a common theme throughout his work and may have grown in importance as he came to understand the importance of convention for semiosis. Peirce appealed to a community of inquirers for his theory of truth, and he regarded the identification with community as fundamental for the advancement of knowledge (the end of the highest semiosis) and, also, for the advancement of human relations. Peirce’s semiotic theory of inquiry is sometimes regarded as a "logical socialism," a view supported by the following provocative remark (in item 25):
Here, then, is the issue. The gospel of Christ says that progress comes from every individual merging his individuality in sympathy with his neighbors. On the other side, the conviction of the nineteenth century is that progress takes place by virtue of every individual's striving for himself with all his might and trampling his neighbor under foot whenever he gets a chance to do so. This may accurately be called the Gospel of Greed.
The sentiment expressed here is similar to that in Peirce’s statement about the significance of the nominalism-realism question for life. Clearly, his brand of realism is opposed not only to nominalism but also to the "gospel of greed" (or what is sometimes referred to as "crass materialism").
This has been, at best, a preliminary sketch of Peirce’s system of thought and of some of the more characteristic of his philosophical doctrines, and much has been left out. For example, there has been no discussion of Peirce’s opposition to determinism (in item 22), or of the intriguing story of his working his way to his guess at the riddle of the universe that led him to his evolutionary cosmology. (30) Little has been said about his lifelong study of mathematics and his nearly lifelong study and practice of experimental science, or of the importance of these for his philosophy. His phenomenology and his theories of esthetics and ethics have barely been mentioned, even though they offer unique and important insights and perspectives for current research, and provide essential support for other parts of his system of thought. His phenomenology has begun to attract widespread attention, and it may turn out that his phenomenological derivation of his categories is of more importance for philosophy than his mathematico-logical derivation. Finally, some scholars might highlight the evolution of his very profound religious views, which are often thought of as completing his metaphysics. It can only be hoped that what has been said here is enough to give a sense of the breadth and profundity—and unity—of Peirce’s philosophical thought, and to inspire the reader to the sometimes difficult but always rewarding study of his writings.
Nathan Houser
1. James Feibleman, "The Relation of Peirce to New England Culture,"
American Journal of Economics and Sociology 4 (1944): 99-107.
back
2. For an account of some of these "get rich schemes," see Christian J. W.
Kloesel, "Charles Peirce and Honoré de Clairefont," Versus 49 (1988):
5-18.
back
3. Whitehead to Charles Hartshorne, 2 Jan. 1936, in Victor Lowe,
Alfred North Whitehead: The Man and His Work, ed. J. B. Schneewind
(Baltimore: Johns Hopkins University Press, 1990), 2:345.
back
4. Hilary Putnam, "Peirce the Logician," Historia Mathematica 9 (1982): 295.
back
5. W. V. Quine, "In the Logical Vestibule," Times Literary Supplement, 12
July 1985, p. 767.
back
6. John Sowa, "Matching Logical Structure to
Linguistic Structure, in Studies in the Logic of Charles S. Peirce
(Bloomington: Indiana University Press, 1992).
back
7. Quoted by James Bird, "A Giant's Voice from the Past," Times
Higher Education Supplement, 8 Sept. 1989.
back
8. Walker Percy, "The Fateful Rift: The San Andreas Fault in the
Modern Mind," 18th Jefferson Lecture in the Humanities, delivered 3 May
1989 in Washington D. C.
back
9. Max H. Fisch, "Peirce at the Johns
Hopkins University," in Peirce, Semeiotic, and Pragmatism (Bloomington:
Indiana University Press, 1986), p. 36.
back
10. See Charles S. Hardwick,
"Peirce’s Influence on Some British Philosophers: A Guess at the
Riddle," in Studies in Peirce’s Semiotic (Peirce Studies 1, Lubbock:
Institute for Studies in Pragmaticism, 1979), p. 27. Ramsey's review of
Wittgenstein appeared in Mind 32:128 (1923): 465-78.
back
11. Arthur F.
Bentley to Joseph Ratner, 1 July 1948. This letter is deposited with
the Bentley Papers in the Lilly Library, Indiana University.
back
12. Max H. Fisch, "Peirce’s Arisbe: The Greek Influence in His Later Philosophy,"
in Peirce, Semeiotic, and Pragmatism, p. 227.
back
13. Gérard Deledalle,
Charles S. Peirce: An Intellectual Biography (Amsterdam: John
Benjamins, 1990), p. xxxi.
back
14. Murray G. Murphey, The Development of
Peirce’s Philosophy (Cambridge: Harvard University Press, 1961), p. 3.
back
15. Francis Ellingwood Abbot, Scientific Theism (London: Macmillan,
1885), pp. 11-12.
back
16. The account of Peirce’s progress toward realism
contained in this and the following eight paragraphs is based on Max
Fisch, "Peirce’s Progress from Nominalism toward Realism," in Peirce,
Semeiotic, and Pragmatism, pp. 184-200; unless otherwise noted,
quotations are from that essay.
back
17. Whether or not Peirce was ever
really a thoroughgoing nominalist or only a more nominalistic realist
than he would be later is discussed by Don D. Roberts in "On Peirce’s
Realism," Transactions of the Charles S. Peirce Society 6 (1970): 67-83.
back
18. Murray G. Murphey, The Development of Peirce’s Philosophy, p. 3.
back
19. Thomas Goudge, The Thought of C. S. Peirce (Toronto: University of
Toronto Press, 1950), p. xx.
back
20. Ibid., pp. 5-7.
back
21. Max H. Fisch,
Introduction to Writings of Charles S. Peirce (Bloomington: Indiana
University Press, 1982), 1:xviii.
back
22. W. B. Gallie, Peirce and
Pragmatism (Harmondsworth: Penguin, 1952), p. 215.
back
23. For example, see
Ilya Prigogine and Isabelle Stengers, Order Out of Chaos (New York:
Bantam, 1984), pp. 302-03.
back
24. My account of Peirce’s cosmological
theory is based, in part, on Peter T. Turley, Peirce’s Cosmology (New
York: Philosophical Library, 1977). Randall R. Dipert, in a review of
Turley (Nature and System 1 [1979]: 134-41), warned that "by shunning
key logical and mathematical issues in Peirce’s writing, certain
important aspects of his writing, such as his synechism, his theory of
relations, and his theory of 'evolving dimensionality' of continua can
hardly be discussed at all. ... Every volume of Peirce’s writing should
perhaps contain the warning: 'Let no one enter here who is ignorant of
logic, mathematics, and the history of science.'" Dipert is no doubt
correct; for without such knowledge, it is not possible to penetrate
fully the depths of Peirce’s metaphysics.
back
25. See David Gruender,
"Pragmatism, Science, and Metaphysics," in The Relevance of Charles
Peirce, ed. Eugene Freeman (La Salle: The Hegeler Institute, 1983):
271-90.
back
26. David Savan, "Toward a Refutation of Semiotic Idealism,"
Semiotic Inquiry 3 (1983): 1-8.
back
27. Thomas L. Short, "What They Said in
Amsterdam: Peirce’s Semiotic Today," Semiotica 60 (1986): 103-28.
back
28.
Joseph L. Esposito, "On the Origins and Foundations of Peirce’s
Semiotic," in Studies in Peirce’s Semiotic (Peirce Studies 1, Lubbock:
Institute for Studies in Pragmaticism, 1979), p. 20. Much of this
paragraph is derived from Esposito's paper, which gives a good
historical introduction to Peirce’s semiotic.
back
29. Christopher Hookway,
Peirce (London: Routledge & Kegan Paul, 1985), p. 246.
back
30. For a brief
rendition of this "intriguing story," see Fisch, "Peirce’s Arisbe," in
Peirce, Semeiotic, and Pragmatism, pp. 229-38.
back
The caret (^) stands for missing punctuation; the tilde (~) represents an unchanged word adjacent to variant punctuation. Line numbers for notes are followed by the letter "n"; line numbers for headnotes are followed by "hn." References to errata located outside the text block are indicated parenthetically below the page number.
| PAGE #.LINE # | ERROR | CORRECTION |
|---|---|---|
| ix.25 | 1 Dec. | 1 July ’67 [1 Dec.] line to be moved after l. 17 in Chronology |
| xxn.6 | 1992 | 1997 |
| 1.14 | univeral | universal |
| 22.16 | reorganizing | recognizing |
| 32.41 | about 11 | about 11¼ |
| 35.10 | or an induction, | and an induction, |
| 97.10 | effect, is | effect, it is |
| 157.33 | correctly | incorrectly |
| 172.21 | thus much | this much |
| 192.6 | is a found | is found |
| 252.12 | C | B |
| 252.13 | B | C |
| 270.5 | attraction | attractions |
| 274.15 | of lawlessness | of absolute [chance] or lawlessness |
| 277.38 | guess of | guess at |
| 286.16 | has | have |
| 287.21 | simply, | simple, |
| 300.23 | comprised6 | compromised |
| 301.10 | wheat-in-itself, our | wheat-in-itself. Our |
| 308.17 | mulitudinous | multitudinous |
| 310.14 | boldly | baldly |
| 337.6 | which actually operates | actually operating |
| 337.31 | c/v2 | c/V2 |
| 338.33 | c/v | c/V̅ |
| 339.30 | a/V | a/V̅ |
| 359.14 | an aesthetics | anaesthetics |
| 385.28 | Delete note 6 (see W8 errata) | |
| 387n. 15 | continuitet | continuiteit |
| 389 c. 2 l. 24 | 373 | 273 |
| 390 c. 1 l. 11 | Bretano | Brentano |
| 393 c. 2 last line | Jourdain, Amable Louis | Jourdain, Philip E. B. |
| 396 c. 2 l. 6 | 85n | 85 |
Readers have asked what was the source of Peirce’s declaration that selections 1 and 3 in EP1 were his two "strongest philosophical works" as quoted in the editorial blurb introducing each selection. The source is found in “Answers to Questions in My Belief in God”, R 845 ISP 25, which reproduces the two sheets of that manuscript Peirce numbered A26 and A27.
|A26|[...] Writing to my brother, I can permit myself to say that my strongest philosophical works were a paper of May 14, 1867, On a New List of Categories, and a paper which appeared some time in 1868 called Some Consequences of Four Incapacities, in which I declared |A27| for scholastic realism. I argued it at more length in the North American Review for October 1871, in a review of Fraser’s edition of Berkeley. Next after these, in strength, were my two connected papers of November 1877, The Fixation of Belief, and Jan 1878 (first written in French on a voyage from Hoboken to Plymouth in September 1877) How to Make our Ideas Clear, in which I enunciated the principle of pragmaticism. I have done a great deal of better work; but none of it has been printed. [...]
R 845 is dated June–September 1905, or summer 1905; Herbert H. D. Peirce apparently encouraged his older brother to write it for a magazine. One can infer that Peirce’s identification of his strongest works is confined to published papers, for he added that he had since then written “a great deal of better work”—presumably even stronger, then—but alas unpublished.
As to the source of Peirce’s declaration that the New List was “perhaps the least unsatisfactory, from a logical point of view, that I ever succeeded in producing,” it comes from R 787 ISP 33 (Peirce’s page 34), “That Categorical and Hypothetical Propositions are one in essence, with some connected matters,” a text Peirce likely wrote in May 1896 (passage published in CP 2.340).
“A man is capable of spiritual consciousness, which constitutes him one of the eternal verities, which is embodied in the universe as a whole.”
Volume 2 of The Essential Peirce provides avid researchers and curious readers with a carefully selected sample of Peirce’s major philosophical texts composed over the last twenty years of his life. Each text gets in its own way to the heart of Peirce’s ever-growing philosophical soul. The volume is intended to fill the pedagogical needs of graduate courses and also the scholarly needs of serious inquirers by making conveniently available texts that have been reliably reconstructed and edited (remembering that EP2, though produced by the Peirce Project, is not per se a critical edition—there is no apparatus—but a high-standard study edition). EP2 has become one of the most extensively referenced works in the scholarship. Along with EP1, it has been translated into Spanish, and a Chinese translation is in the works. Nathan Houser authored the introductions to both EP1 and EP2. Readers are especially encouraged to read his introduction to EP2, for it is a masterpiece that manages to reduce the manifold strands of a complex volume to illuminating unity.
A number of major philosophical themes traverse the entire volume. This overview will focus on four possible paths of exploration: those labeled semiotics, pragmatism, evolutionary philosophy, and the art of reasoning. Each path takes its start in EP1 before plunging wholeheartedly in EP2.
To begin with, anyone contemplating teaching or studying Peirce’s semiotics will be very well served in EP2. If one’s purpose was to teach the evolution of Peirce’s semiotic theory in chronological order, the first thing would be to start with a few texts in EP1: the first ten sections of “On a New List of Categories,” which explain and demonstrate the non-arbitrary root of the categorial scheme that presides over semiotic distinctions while also describing the method of prescision as a special tool of non-reciprocal conceptual separation that justifies the hierarchical structure of categories; some key “questions” from “Questions Concerning Certain Faculties Claimed for Man” that argue beyond controversy why every train of thought relies on the operation of mediating signs without exception; the first section of “On the Algebra of Logic,” which usefully connects elementary semiotic concepts to the logic of relations; and the first chapter of “A Guess at the Riddle” which generalizes the 1867 categories to universal applicability in the realm of inquiry.
That done, EP2 can then be transformed into the principal semiotics textbook. Selections 2 (“What Is a Sign?”) and 3 (“Of Reasoning in General”) provide Peirce’s mid-1890s clear views about the fundamental distinctions between icon, index, and symbol. This lighter interlude is an efficient springboard toward the core semiotic texts found in the 1903 “Syllabus of Certain Topics of Logic,” specifically in selection 20 (“Sundry Logical Conceptions”), which emphasizes the second and third trichotomies (not knowing there is a trichotomy prior to them): icon/index/symbol and sumisign/dicisign/argument or suadisign, and discusses dicisigns extensively; and in selection 21, “Nomenclature and Divisions of Triadic Relations,” which starts with an essential, though ultra-condensed, aperçu into the logic of triadic relations, before ushering in a brand-new trichotomy, qualisign/sinsign/legisign—in part an elegant theoretical solution toward the classificatory problem presented by the unwieldy and short-lived, even if powerful, distinction between the three hypoicons called image, diagram, and metaphor in selection 20. Selection 21 is a rich mine of fundamental semiotic distinctions: it presents and exemplifies the nine types of sign functions distributed among the three trichotomies, and shows how they connect together according to strict hierarchical categorial rules to form ten classes of signs, each one of which corresponds to a distinct set of precise questions that buttress a systematic process of inquiry. Once that is covered, several possibilities are open for continued learning in the later texts. The core of “variant 1” in selection 28, “Pragmatism,” introduces the capital idea of collateral observation, itself indispensable for the ensuing distinction between two types of objects, immediate and dynamic. Peirce also distinguishes between three types of interpretants, emotional, energetic, and logical, and redefines more fully the general concept of sign while also giving birth to the notion of “semiosis.” Selections 32 and 33 (letters to Lady Welby and William James) also abound with capital theoretical complements regarding every sign component and classification, including the distinction between immediate, dynamic, and final interpretants, and the expansion of the classification to 66 classes of signs (really, 66 sets of heuristic questions). Semioticians wanting to deepen their understanding of symbolicity will want to study minutely sections 3 and 4 of part III of selection 22, “New Elements.” Those who want to delve into Peirce’s conception of communication and rhetoric will want to learn by heart section 23, “Ideas, Stray or Stolen, about Scientific Writing,” before moving on to section 9 of selection 27, “The Basis of Pragmaticism in the Normative Sciences,” and relevant parts of the letters to Lady Welby.
If one’s purpose was to study the development of Peirce’s pragmatism, one would of course begin with some of the celebrated texts in EP1 in order to whet the appetite for learning. These could include selections 2 and 3, which are necessary to weaken any Cartesian impulse one might have while reinforcing scholastic-realist propensities, and then selections 7, “The Fixation of Belief,” and 8, “How to Make Our Ideas Clear,” to achieve a clear grasp of the foundational stakes: what is the best method of inquiry, how, and why; what is the range of the knowable, what does it take to express it adequately, what would be an especially powerful logical maxim in that regard, and how should it be wielded with what kind of benefits? Other texts from the “Illustrations of the Logic of Science,” such as those dealing with chance and probability, should be studied to convey the importance of adopting an indeterminist and fallibilist approach when inquiring about the order of nature in a scientific spirit.
From there, one can then move to EP2 and focus on the 1903 Harvard Lectures on Pragmatism, dwelling there for a long time (depending on one’s particular intentions), making sure, minimally, to study selections 10 and 14–16, that is, lectures 1, “The Maxim of Pragmatism,” 5, “The Three Normative Sciences,” 6, “The Nature of Meaning,” and 7, “Pragmatism and the Logic of Abduction.” Those lectures were Peirce’s first public occasion to explain his own original version of pragmatism to an audience mostly versed in William James’s approach. Peirce, being the fundamental inquirer he has always been, goes to the phenomenological and normative core of the subject and analyzes it in exquisite details, with a logical depth unmatched by any other pragmatist. One of his aims is to provide pragmatism with a logical foundation that, if well understood and improved upon with further investigation, should make that particular –ism far less arbitrary than any other –ism in intellectual history. That aim is buttressed by five later texts in EP2 well worth the slowest of readings: selections 24 to 28, some of which see Peirce turning pragmatism into pragmaticism precisely to save it from weaker versions too prone to fall to nominalistic reductionisms. Those texts are part of Peirce’s agenda to provide a logical proof of pragmaticism, the central strategy of which is to rephrase the pragmatic maxim into the form of an explicit semiotic theorem, and to show how it follows from a set of premisses anchored in phaneroscopy, in the theory of perception, and especially in semiotics.
A course on Peirce’s evolutionary philosophy could take the following path. It, too, naturally, ought to begin in EP1, starting also with the anti-Cartesian texts of 1868, since evolutionism brought with it a number of logical and metaphysical consequences, including the relegation of dualistic theories from the broadly speculative realm (where they failed) to the narrowly practical realm (where they are useful within the analytical limits of data collection), the necessity to focus afresh on such indispensable conceptions as infinity, generality, and continuity; the duty to reinvent metaphysics, redefine reality, and resurrect the conception of truth within the context of an indefinite process of inquiry turned social. Reading Peirce’s Berkeley review-article is then the next thing to do, for evolutionary theory requires the adoption of a refreshed, thoroughgoing, scholastic realism. “Illustrations” texts such as “The Doctrine of Chances” and “The Order of Nature,” complemented by Peirce’s 1884 lecture on “Design and Chance,” gives readers the occasion to grasp how Peirce’s thought is itself fast evolving, under the influence of many books and discussions with the intelligentsia of the time. Evolutionism implies that nature is not uniform, contra all determinists. Peirce’s 1887-88 “Guess at the Riddle” should be read entire, not only to understand his three-category theory (an indispensable requisite), but to appreciate how those categories are actually at work both in nature and in the inquiry about nature, including especially of course the processes of, and theories of, evolution. Those readings provide then an effective introduction to the five texts of the “Monist Metaphysical series,” and the reader may want to focus especially on “The Doctrine of Necessity Examined” (for the sake of Peirce’s tychism), “The Law of Mind” (for his synechism and the consequent objective idealism), and “Evolutionary Love” (for his agapism, which he never abandoned).
All of that covered, the reader can then turn to EP2 and begin, for the sake of continuity, with the first text, “Immortality in the Light of Synechism.” After this, there are several possible paths, one of which is to read together sections 7, “Laws of Nature,” and 9, “On Science and Natural Classes,” which are tightly connected: they are all about the reality of laws and the inquirer’s capacity to express those laws and how they get to replicate themselves under the appearance of natural classes, which Peirce redefines teleologically. Peirce’s conception of teleology (final causation) is at the core of his evolutionary philosophy, and an adequate understanding of it is another passage obligé. The course of study from here can move on to the 1903 Harvard Lectures, first to get acquainted with Peirce’s mature theory of the categories (lectures 2 and 3), and then with his mature realism (lecture 4, “The Seven Systems of Metaphysics,” in which the seventh is of course the only one capable of accommodating a complete evolutionary philosophy). Having reached that point, the reader may want to finally cap his or her experience with a thorough reading of Peirce’s “New Elements,” which ends with a semiotic theory about the origin of the evolving universe that is one of Peirce’s greatest gifts to future inquiry.
A semester-long class in Peirce’s logic of reasoning could, too, take multiple paths, depending on one’s logical proclivities, which could edge more toward formal logic or more toward Peirce’s broader semiotic logic. A middle path would focus on Peirce’s theory of inferences and inquiry. That topic reflects Peirce’s lifelong philosophical quest as much as any of the other suggested three.
Starting with EP1, the exploration could start with studying Peirce’s discussion of the consequences of the first two “incapacities” in selection 2 (EP1: 30–38) before tackling selection 3, “Grounds of Validity of the Laws of Logic,” which contains Peirce’s inaugural attempt to ground the validity of both hypothesis and induction, ending with provocative insights into the self-sacrificial nature of logicality well considered, that is, in the light of the ultimate purpose of increasing knowledge for the welfare of the future overarching society of inquirers. From there, moving to the last three 1878 papers on “The Probability of Induction,” “The Order of Nature,” and “Deduction, Induction, and Hypothesis” would no doubt be wise, considering their focus on the three kinds of reasoning. Selection 14, “Introductory Lecture on the Study of Logic,” provides a good reminder of the role logic ought to play in a sound liberal education.
Moving on to EP2, the third essay, “Of Reasoning in General,” emphasizes the need to keep in mind that a proper account of reasoning cannot really eschew Peirce’s semiotic theory, since the stuff reasoning is made of consists of signs and their continuous concatenations subjected to “prescissive” categorial rules. The fourth essay, “Philosophy and the Conduct of Life,” provides a highly readable philosophical interlude that puts reason into its proper place, without ignoring the significance of instinct and sentiment. Essay 5, “The First Rule of Logic,” is just as wonderful; it compares the role of observation in the three types of inferences, extolls the first rule of reason that in order to learn one must desire to learn and not be merely satisfied with what one is already inclined to think; it draws the famous corollary that adorns the header of this website, “Do not block the way of inquiry.” That motto finds multiple expressions in Peirce’s writings, and his philosophy can be seen as the continuous demonstration of that motto for the sake of our future—the future of humanity but also of the summum bonum known as concrete reasonableness. Armed with such a sound principle, the invigorated reader will then be in a good position to examine Peirce’s prodigious 1901 essay “On the Logic of Drawing History from Ancient Documents,” where he gives, among many things, a sustained discussion of the logic of science, outlining many nuances of the different kinds of reasoning, including two types of deduction (corollarial and theorematic) and three types of induction. Peirce also gives a solid account of the economic and other factors that bear on the selection of historical hypotheses. Pragmatism being the core maxim of logic, some foray into the 1903 Harvard Lectures is advisable, especially the last three. We are reminded that reasoning is a form of action relative to aims and is thus subject to ethical considerations, especially the need for self-control. Peirce explores the logical goodness of different types of reasoning, and returns to the consideration of generality, which pours in upon us in our perceptual judgments. Deduction, Induction, and Abduction get connected to the modalities of being, and the pragmatic maxim, having to do with meaning and purpose, is viewed in light of the teleological process of interpretation that is at the core of every inferential process, right from the start—thus right within perception itself. That reasoning begins in perception is the stone that sharpens the edge of Peirce’s famous three cotary propositions. Peirce emphasizes especially the role of abduction within perception and holds that pragmatism itself is tantamount to the logic of abduction.
Once the reader keen on learning more about the art reasoning leaves the Harvard Lectures, the next text that will immediately solicit his or her attention is the inaugural Lowell lecture appropriately titled “What Makes Reasoning Sound?” Peirce refutes therein the hideous idea that reasoning rests on a feeling of logicality and that there is therefore no distinction between good and bad reasoning. He shows that good reasoning tends to speed up the march toward truth, that we have a natural (evolutionary) tendency to guess correctly, and that such progress depends on deliberate, self-controlled conduct. Finally, the last two pre-Appendix selections in EP2, “A Sketch of Logical Critics” and “An Essay toward Improving Our Reasoning in Security and Uberty,” will reward the assiduous researcher with late-life considerations about the theory of the kinds and degrees of assurance afforded by the three kinds of reasoning, about the contrast between reasoning and experience, and the trade-off reasoning involves between security and “uberty,” a neologism alluding to the rich suggestiveness and fruitfulness of abductive reasoning.
“I become aware that though ‘universe’ and ‘awareness’ are one and the same thing, yet somehow the universe will go on in some definite fashion after I am dead and gone, whether I shall be the least aware of it, or not.”
Chronology xi
Preface xiii
Introduction by Nathan Houser xix
CONTENTS
1. Immortality in the Light of Synechism (1893) 1
2. What Is a Sign? (1894) 4
3. Of Reasoning in General (1895) 11
4. Philosophy and the Conduct of Life (1898) 27
5. The First Rule of Logic (1898) 42
6. Pearson's Grammar of Science (1901) 57
7. Laws of Nature (1901) 67
8.
On the Logic of Drawing History from Ancient Documents,
Especially from
Testimonies (1901) 75
9. On Science and Natural Classes (1902) 115
HARVARD LECTURES ON PRAGMATISM (1903)
10. The Maxim of Pragmatism (Lecture I) 133
11. On Phenomenology (Lecture II) 145
12. The Categories Defended (Lecture III) 160
13. The Seven Systems of Metaphysics (Lecture IV) 179
14. The Three Normative Sciences (Lecture V) 196
15. The Nature of Meaning (Lecture VI) 208
16. Pragmatism as the Logic of Abduction (Lecture VII) 226
LOWELL LECTURES ON LOGIC
17. What Makes a Reasoning Sound? (1903) 242
A SYLLABUS ON CERTAIN TYPES OF LOGIC (1903)
18. An Outline Classification of the Sciences 258
19. The Ethics of Terminology 263
20. Sundry Logical Conceptions 267
21.
Nomenclature and Divisions of Triadic Relations,
as Far as They Are Determined
289
22. New Elements (Καινὰ Σ𝜏οιχει̑α) (1904) 300
23. Ideas, Stray or Stolen, about Scientific Writing (1904) 325
PRAGMATICISM (1905-07)
24. What Pragmatism Is (1905) 331
25. Issues of Pragmaticism (1905) 346
26. The Basis of Pragmaticism in Phaneroscopy (1906) 360
27. The Basis of Pragmaticism in the Normative Sciences (1906) 371
28. Pragmatism (1907) 398
29. A Neglected Argument for the Reality of God (1908) 434
30. A Sketch of Logical Critics (1911) 451
31. An Essay toward Reasoning in Security and Uberty (1913) 463
APPENDIX: SEMIOTICS FROM LATE CORRESPONDENCE
32. Excerpts from Letters to Lady Welby (1904-08) 477
33. Excerpts from Letters to William James (1909) 492
Notes 503
Index 557
R 886. [First published in CP 7.565-578. This is an article Peirce sent to Paul Carus on 4 May 1893, hoping to have it published in the Open Court but suggesting that it was “almost worth keeping for the Monist.” Carus agreed to publish it in the Monist, but a series of misunderstandings between the two men arose at the same time concerning both a matter of honorarium and Peirce’s refusal to let Carus publish a private letter about the efficiency of prayer. Peirce was mistakenly led to believe that Carus did not want to publish the article, and he effectively withdrew it when he broke off correspondence in June 1893.]
Origin of the Text
On April 9, 1893, Peirce wrote to Paul Carus, Open Court editor, a long letter criticizing the latter’s “homiletic writing” and discussing the efficiency of prayer. Carus, who loved a good controversy, decided to publish the letter; he had it set into type, and sent a galley to Peirce at the beginning of May, while working himself on a reply, the 9-page penciled draft of which is in the archives of Southern Illinois University (Carbondale). In a letter dated May 5, Peirce thanked Carus for his flattering gesture, but asked him not to publish the letter, principally because it was exaggerated in tone and not fit for publication. A few days earlier Peirce had sent Carus an article entitled “What is Christian Faith?” to be published in the Open Court, which Peirce thought bore on pretty much the same subject, and the day before, on May 4, Peirce had sent another article, also intended for the Open Court, entitled “Immortality in the Light of Synechism.” In the same May 5 letter to Carus, Peirce wrote (L77): “I have besides lately sent you two pieces for the Open Court. One of them [“What is Christian Faith?”] says pretty much the same as this [April 9] letter; and the other which I sent yesterday [“Immortality in the Light of Synechism”] contains some valuable matter,—almost worth keeping for the Monist.” Carus acknowledged receipt of the “What is Christian Faith?” article in a May 4 letter (which Peirce received on May 10), and told Peirce that Hegeler wanted to know what the honorarium would be for it. On May 9, 1893, Carus acknowledged receipt of both the article on Synechism and the 5 May letter, and agreed that the Synechism article was suited for The Monist (L77: 74). He also expressed his disappointment at Peirce’s refusal to have his April 9 letter published, telling Peirce he liked the directness of it. On May 10 Peirce received Carus’s letter of May 4 and replied immediately, taking umbrage at Hegeler’s asking what would be the honorarium for the “Christian Faith” article.
Peirce thought Hegeler was recanting the terms agreed upon regarding the articles in the “Critic of Arguments” series. Apparently, Peirce thought that any article he would submit to the Open Court, whether as part of the “Critic of Arguments” series or not, would be paid on the same terms. This must not have been Hegeler’s understanding. Peirce wrote, “I infer that the terms hitherto agreed upon for the Critic of Arguments no longer meet his [Hegeler’s] views. In that case, it will only be necessary to return to me the two articles sent. I was to have mailed you today two more papers for the Critic of Arguments; but I can print them elsewhere.” It thus seems that Peirce’s short temper gave rise to a misunderstanding between him and Carus. [Peirce had many dealings with the Open Court going on at the same time; one was the translation of Mach’s Mechanics in collaboration with Thomas McCormack; another was his dealings with Hegeler regarding the publication of an elementary arithmetic, and also of two other books, one a collection of his logic papers, and another a reprinting of his “Illustrations of the Logic of Science.” Yet another matter had been the discussion with Carus about the printing of the article “Reply to the Necessitarians,” written in a very frank, irritated style.] On May 13 Peirce received Carus’s May 9 letter and wrote back a long and irate reply, accusing Carus and Hegeler of sectarianism. The letter ended thus: “I should have no objection to expressing my ideas about prayer for the Open Court, should it be decided that I write for it any more. Mr. Hegeler has to decide whether he wishes to pay the same price as heretofore. If so, and if you want articles from me on religious topics, I will give my views on prayer. But my private letters are hastily written and are not intended for the public.” Carus replied on May 19, obviously irritated but trying to appease Peirce, that Peirce was right and that his letter better remained unpublished: “it is better to confine myself only to the matured productions of your pen. Perhaps I am to be blamed that I have taken your letter too seriously. Concerning the honorarium for your articles Mr. Hegeler will write you himself.” [Note that through this entire episode Peirce was conducting a separate correspondence with Hegeler about the production of his arithmetic book, and Hegeler was sending Peirce several $250.00 checks as advances for it.]
Not really appeased, Peirce wrote back on May 23, asking bluntly (1) whether or not the Open Court desired his exposition of the philosophy of prayer on the same terms as before, and (2) whether or not he could submit a series of four articles for the Monist in continuation of the exposition of his philosophy, these articles to appear within five numbers with the advanced agreement that they shall appear. Carus replied on May 27. An unsent letter so dated in the SIU archives simply stated the following: “Having come to the conclusion not to publish your articles in The Open Court, I take the liberty to return them to you.” But before signing it Carus had a change of heart (maybe because he received Peirce’s letter later that day) and wrote instead that (1) he had to decline (without elaboration) Peirce’s offer of a new Monist series of articles, and that (2) he did not want Peirce to write on the philosophy of prayer on the grounds that Peirce had refused the printing of his April 9 letter where his philosophy of prayer was set forth already (L77: 83). But Carus kept the two articles on Christian faith and on Synechism, “which do not touch upon the subject of prayer.” On June 5 Peirce wrote a letter to Hegeler (no longer extant) in which he asked whether the Open Court desired further articles in the “Critic of Arguments” series. Hegeler passed the letter on to Carus, who replied on June 10 that Peirce could send articles, but that the Open Court preserved the liberty of rejecting them. Carus added that he intended to publish “Immortality in the Light of Synechism” in the Monist, that “What is Christian Faith” was in the hands of the compositors, and that a third paper, “The Critic of Arguments,” which Peirce had sent to Hegeler simply for inspection and not for publication, could be published in two months if it could be shortened a little. Carus enclosed the first and third articles with his letter, asking Peirce to return them in case he was satisfied with the proposed arrangement (L77: 87). Peirce may not have read Carus’s good letter carefully and may have thought that the two articles had simply been rejected. He broke off correspondence, never sending back the articles.
“What is Christian Faith” appeared in the Open Court on July 27, 1893, and “Reply to the Necessitarians,” which had been ready by March, appeared in the July Monist. Correspondence resumed only one year later, with Peirce sending a confidential letter on June 25, 1894, asking Carus the reason of his rancor against him (Carus had just published a satire on “circle-squarers” which Peirce mistakenly thought was aimed at him) and with Carus acknowledging Peirce’s “enigmatic letter” and telling him “I cherish not the slightest animosity toward you and on the contrary am very sorry that you broke off our correspondence so suddenly. . . . My last letter had reference to several MSS of yours which we accepted, one for The Monist, the others for the Open Court. I returned the MSS to you at Mr. Hegeler’s suggestion, so as to have you at liberty to keep or return them. I told you so in my letter. I have neither received the MSS back, nor did I hear from you again” (July 1st, 1894, L77: 97). Encouraged by this reply, Peirce submitted new manuscripts to Carus, but by this time Hegeler, who owned both The Monist and the Open Court, felt some animosity toward Peirce (who never finished his arithmetic book) and told Carus to refuse any manuscript from Peirce. Carus announced this to Peirce on July 16th, 1894, adding “I must return your MSS and can do nothing except to hope that you will pull through” (L77: 103).
R 404. [Partly published in CP 2.281, 2.285, 2.297-302. This document, probably composed early in 1894, was originally the first chapter of a book entitled “The Art of Reasoning” which Peirce submitted in mid-June 1894 to Ginn & Co. The publishers rejected it, fearing it could not sell as a textbook. Thereupon Peirce reconceived the entire plan of his work, retitling it “How to Reason: A Critick of Arguments” (also known as “Grand Logic”). “What is a Sign?” became Chapter 2 and was repaginated accordingly. It follows “Chapter I. The Categories” (R 403), and these two chapters together constitute the first division “Formal Study of General Logic” of the first book “Of Reasoning in General” of the entire work.]
R 595. [Partially published in CP 2.282, 2.286–291, 2.295–296, 2.435–444, and 7.555–558. Soon after Ginn & Co. rejected Peirce’s “How to Reason,” George A. Plimpton, a publisher in that company, encouraged Peirce to write “ a logic after the plan of Jevons, not any larger than that,” adding that, “as a text-book, pure and simple, it would have a good sale.” About a year later, probably in the summer of 1895, Peirce began composing the smaller book, which he titled “Short Logic.” “Of Reasoning in General” is the first and only chapter he wrote for that book. He sent it for comments to William James, Josiah Royce, and Francis E. Abbot. The latter responded that it was a “masterly piece of work,” an opinion Peirce echoed later to his friend Francis Russell by saying it was his “best statement” of his division of signs into Icons, Indices, and Symbols. The chapter is divided into 13 articles. Of Article 9, which presents a long discussion of certain logical-grammatical features of the Egyptian and other languages, only the first and last paragraphs are presented here.]
R 437. [Partially published in CP 1.616–648; fully published in Reasoning and the Logic of Things, pp. 105–122. Of the eight Cambridge Conferences Lectures Peirce delivered in February and March 1898, this was the first one, given on 10 February 1898. Peirce finished composing it on January 30, substituting it to another opening lecture William James had convinced him not to give (see WJ–CSP, 1/23/1898), which Peirce had titled “On Detached Ideas in General, and on Vitally Important Topics as such” (R 435).]
R 442 AND R 825. [Published, in part, in CP 5.574–589 and 1.135–140, and with some variations in Reasoning and the Logic of Things pp. 165–180. This is the fourth of the Cambridge Conferences Lectures, which Peirce delivered on February 21, 1898. William James, who had read it a month earlier, told Peirce it was “a model of what a popular lecture ought to be” and implored him “on bended knees to give it first.” Peirce instead rewrote his first lecture and kept this one in its fourth place, but altered it with many revisions. He deleted a number of passages, mostly because of time constraints (all but two have been restored), and added seven paragraphs (the three pages of R 825, which begin the famous statement of the one rule of reason, “Do not block the way of inquiry”) which have been inserted at their most likely place in the middle of the lecture.]
P 802: Popular Science Monthly 58 (January 1901): 296–306. [Published in CP 8.132–152. Peirce thought this text was his best written work (L378:5). Its complete title includes the subtitle “Annotations on the First Three Chapters” (but some remarks are made on the fourth chapter as well). Peirce’s review (P 501) of the first edition of Pearson’s book appeared in The Nation in July 1892 (Contributions to The Nation 1:160-161). Of the second edition of The Grammar of Science (published by Adams & Charles Black, London, 1900) Peirce published a short, negative notice (P 725) in The Nation on 15 March 1900 (Contributions 2:237). On 10 March 1900, James McKeen Cattell, the editor at the time of both the journals Science and The Psychological Review (and, two months later, of the Popular Science Monthly) wrote Peirce to ask him to write a review of Pearson’s book for the Psychological Review. Peirce agreed immediately and began to collect reading notes for the purpose (they survive in MS 576). On April 2 he asked Cattell what should be the length of the review, given that it “will be important since the book is much used and I shall be able to show that its doctrine is in important respects altogether untenable.” Cattell answered promptly that Peirce could have all the space he wanted, a long and thorough review being expected. Peirce, however, was unable to write the review before October, too late for the November issue. Cattell suggested then that “in view of the general interest of the review, it might be printed to advantage in the Popular Science Monthly”—albeit for a lesser pay. Peirce agreed, thinking that it would provide better publicity, and added that he wanted to write a second article to deal with some of the other chapters (he never did). A complete draft with important variations (some published in CP 8.136 n3 and 8.153–156) is found in R 1434.]
MS and TS from the Smithsonian Institution Library (doc. 3804.10) [Published in Philip P. Wiener’s Charles S. Peirce: Selected Writings, pp. 289–321. Only the first four sections (out of eleven) are printed here, of a text titled originally “Hume on Miracles and Laws of Nature.” On April 3, 1901, Samuel P. Langley, Secretary of the Smithsonian Institution, invited Peirce to write a very short article “on the ‘Laws of Nature,’ as understood by Hume’s contemporaries and by our own, with special reference to his argument on miracles.” Although Peirce was not thrilled by the subject, convinced as he was that there was no connection between Hume’s argument and the idea of a law of nature, he tried to comply with Langley’s wishes as best as he could. In two months, he produced no less than seven texts, three of which he submitted to the Secretary.* Langley rejected the first two on the ground that they were too difficult to the readers of his annual Report. The third one (sent on June 1) he judged more acceptable but too long, and he had it typed with many excisions and revisions in his own hand. Peirce received the typescript on July 19, and revised it with several important additions a few weeks thereafter; he sent the document back to Langley in early September. For reasons unknown, Langley finally decided not to publish it, and substituted a paper of his own on “The Laws of Nature.” The following text reproduces Peirce’s autograph manuscript and incorporates those of his corrections to the typescript that were not forced by Langley’s alterations.]
*Not counting the present document, here is the probable chronological order of the first six manuscripts:
(1) R 872, “The Idea of a Law of Nature among the contemporaries of David Hume and among advanced thinkers of the present day.” Written between April 4 and 10, 1901, this is the first text Peirce sent to Langley (on April 11, 1901); it was reviewed for Langley, negatively, by Lester F. Ward. Langley rejected it on April 19. Published in Historical Perspectives II: 880-889.
(2) R 873, “Hume’s Argument against Miracles, and the Idea of Natural Law.” An unfinished text probably composed around April 20, 1901. Published in Historical Perspectives II: 904-912.
(3) R 869, untitled, marked “H[ume] on M[iracles].” Probably composed toward the end of April 1901 as a working document toward the next one. Published in CP 6.522-547.
(4) R 692, “The Proper Treatment of Hypotheses: a Preliminary Chapter, toward an Examination of Hume’s Argument against Miracles, in its Logic and in its History.” This was the second paper Peirce sent to Langley, who received it on May 13, 1901. Peirce wanted it to be the first of three chapters. Langley rejected the paper and the plan on May 18. Published in Historical Perspectives II: 890–904.
(5) R 870, “What is a Law of Nature?” (title suggested by Langley). A very interesting document, preliminary to the final version; composed around May 20, 1901.
(6) R 871, “Laws of Nature and Hume on Miracles.” Composed at the end of May 1901, this is the complete draft of the final Smithsonian document.
R 690. [Only the first half of the MS is printed here; it was published in CP 7.164–231 and in Historical Perspectives on Peirce’s Logic of Science, Part II, pp. 705–762. In the second half Peirce discusses three examples drawn from Aristotle (CP 7.232–255), Plato, and Pythagoras (Historical Perspectives pp. 763–800). On 13 May 1901 Samuel P. Langley, Secretary of the Smithsonian Institution, received Peirce’s second attempt at writing a paper on Hume’s argument against Miracles, titled “The Proper Treatment of Hypotheses” (R 692). Langley rejected it because of its complexity. A draft of it reveals the first title Peirce had in mind: “On the Principles which ought to Guide us in Accepting or Rejecting Historical Testimony.” Peirce wanted to develop this into three chapters, the second of which would have shown “how the principles of minute logic are to be applied in dealing with historical documents.” Since Langley would not allow it, Peirce turned a few months later to his friend Francis Lathrop, an artist, for whom he had just written a paper on “University.” Lathrop agreed to help find sponsors for a Logic book Peirce proposed to write. By the end of September Peirce had submitted the first chapter, and on October 22 Lathrop wrote Peirce to express his hope that the arrangement could be carried through, at $150 a chapter, and asked for four more chapters, “the first of which could be the one which you spoke of having now in hand ‘On the Logic of Inference from Ancient Documents.’” Soon thereafter, on Nov. 1, Peirce wrote to the Secretary of the National Academy of Science, Ira Remsen, about his intention to attend the November meeting in Philadelphia “to present a long paper ‘On the Logic of Research into Ancient History.’” He added that he already had 27,000 words written, which he hoped to have typed before the meeting, and that he wanted to present a 40-minute abstract—which he eventually did. A note dated December 3 from Lathrop’s secretary, H. A. Hammond Smith, indicates that a long document Peirce had recently sent was being typed in Smith’s office. Internal evidence shows that this was “The Logic of Drawing History,” which is extant both as a manuscript and as a typescript corrected by Peirce. The text here published is a transcription of the manuscript emended from the typescript. Many draft pages survive in R 691. A draft of Peirce’s report of the N.A.S. meeting, with an account of his own paper, is found in R 1443 (partly published in CP 7.162–163), and the report itself, perhaps not fully authored by him, was published in The Nation on 21 November 1901 (Contributions III: 53–57).
R 427. [The part printed here was first published, with somewhat different omissions, in CP 1.203–237. It comes from Peirce’s projected book “Minute Logic,” Chapter II, “Prelogical Notions,” Section 1, “Classification of the Sciences.” R 427 was composed between February 20 and April 4, 1902, and the portion below was written February 20–26, 1902. An earlier draft subsists in R 426, and an elaborate abstract by the author is in R 1344. “Minute Logic” is a book that was commissioned by Peirce’s friend Francis Lathrop. Lathrop paid Peirce $150 for each chapter (in exchange for the copyright) and had them typed. No typescript for this chapter has been found. The side-notes were written by Peirce in the margin of the manuscript, probably to emulate the many side-notes that were inset in the text of Auguste Comte’s Philosophie positive.]
R 301 [Published in CP 5.14–40 and in Turrisi 1997: 109–121. The first lecture, left untitled by Peirce, and composed some time after March 16, 1903, was delivered on Thursday, March 26, 1903. Advertised in the Harvard University Calendar as the “Introduction” to the series of lectures, R 301 discusses the advantages of pragmatism as a logical method of inquiry—hence the title here given to it. Peirce wrote no draft of the first lecture.]
R 305 and R 306. [Published with omissions in CP 5.41–56 and 5.59–65 and in Turrisi 1997: 150–165. The second lecture was delivered on Thursday, 2 April 1903, under the Harvard Crimson-advertised titled of “Phenomenology or the Doctrine of Categories.” What document Peirce read at the lecture is not entirely clear. His first plan had been to discuss mathematics and to show how an analysis of the mathematical reasoning could lend support to pragmatism. He wrote two different versions of a lecture to that end (R 302–303, published in Turrisi 1997: 123–138) but then realized he could not afford the time needed to do justice to such a formidable subject. He thus abandoned it and turned his efforts to an explanation of his phenomenology. Three documents relating to that effort have survived. The first is R 304, “On Phenomenology” (published in Turrisi 1997: 139–150), but Peirce rejected it with the self-injunction “To be rewritten and compressed.” This leaves us, on the one hand, with R 305, the second draft, also titled “On Phenomenology,” which Peirce at some point seems to have wanted to reject, as he wrote “This won’t do it will have to be rewritten” at the top of the first page, and, on the other hand, with R 306, labeled “3rd Draught” and titled “On Phenomenology, or the Categories”—a title closer to the Crimson advertisement. A red-ink note at the beginning of R 306 explains Peirce’s intention to begin by making a first draft about the third category, and then to compress what he wanted to say about the first two categories according to the amount of time he might be left with. Obviously Peirce was getting distressed (he quotes Polonius’s “Tis true ’tis pity | and pity ’tis ’tis true” in Hamlet II.ii.97–98). R 306 is incomplete, as the 12 pages it contains barely touch the matter of the third category, and this leaves us with the possibility either that Peirce used both R 305 and R 306 for his lecture, or that there was another, final, version that did not survive. The text that follows conflates the two manuscripts.]
R 308. [Partly published in CP 5.66–81 and 88–92, and in Turrisi 1997: 167–188. Peirce delivered the third lecture on Thursday, April 9, 1903. It was announced both in the Harvard Crimson and the Harvard Calendar under the erroneous title “The Application of the Category to Pragmatism” (“Category” should have been in the plural), with a pressing invitation to those who missed the second lecture to come and read the manuscript of it before attending the third. A complete draft of R 308 is found in R 307, titled “The Categories continued.”]
R 309. [Published in parts in CP 5.77n, 5.93–111, 5.114–118, 1.314–316, 5.119, 5.111–113, and 5.57–58. Also published in Turrisi 1997: 189–203. This lecture, which might as well be titled “The Seventh System of Metaphysics” since Peirce never fulfills his intention of discussing the first six systems for lack of time, was delivered on Thursday, April 16, 1903. R 307 is a complex document, spread over two notebooks, with many passages either skipped or rewritten on facing pages. The text that follows incorporates all of Peirce’s revisions and restores the last version of all skipped passages. The reader will find in the endnotes a transcription of those earlier deleted or skipped passages that were deemed significant enough.]
R 312. [Published in CP 5.120–150 and in Turrisi 1997: 205–220. Peirce delivered the fifth lecture on Thursday, April 30, 1903, two weeks after Lecture 4 (the university had been in recess the previous week). Peirce did not title the fifth lecture, but the Harvard Crimson announced that he would be discussing the normative sciences, “generally considered to be logic, ethics, and aesthetics,” and that he then would proceed to a discussion of “truth” and “meaning.” Two short drafts of the lecture can be found in R 310 and R 311. The opening section of R 312, which amounts to its first ten pages, was skipped by Peirce at delivery time; in it Peirce describes his fascinating and exacting research methodology. Since this is discussed again at the end of the lecture, albeit more briefly, we do not restore the first section in the main text, but reproduce it in an endnote.]
R 314 and R 316. [First three sections published in CP 5.151–179; published entirely in Turrisi 1997: 221–239. The sixth lecture was delivered on Thursday, May 7, 1903. The Harvard Crimson announced it under the title “The Nature of Meaning,” which must have been provided by Peirce (the manuscript bears no title). This was supposed to be the last lecture of the series, but Peirce, seeing that he would have no time to bring his topic to a satisfactory closure, was allowed to give an extra lecture the following week. Lecture 6 is divided into four sections (the fourth is R 316), and a note scribbled by Peirce on the cover of the notebook, “(first 35 pages as delivered),” indicates that he read the first two sections completely, but ran short of time and only glossed over the last two sections. An important draft of Lecture 6, with many significant passages not repeated in the final version, survives in R 313.]
R 315. [Published in part in CP 5.180–212; in full in Turrisi 1997: 241–256. Delivered on Thursday, May 14, 1903, this supplementary lecture concludes the series (an eighth one was improvised the next day on “multitude and continuity,” but this was a complementary lecture mostly intended for students of philosophy and mathematics). Peirce gave no title to Lecture 7. The Harvard Bulletin announced only that Peirce would “give the summary of his previous lectures” and “put in clearer light the relation of the views maintained to the general doctrine of pragmatism.”]
R 448–449. [Partly published in CP 1.591–610 (R 448), 1.611–615 and 8.176 (R 449). Delivered on Monday, November 23, 1903, this is the first of eight lectures Peirce was invited by A. Lawrence Lowell, in mid-March 1903, to give at the Lowell Institute in Boston during the fall. The title for the course was “Some Topics of Logic bearing on Questions now Vexed.” The first lecture was probably composed in late August–early September, and several drafts have survived: the first in R 447, the second in R 452, the third in R 451, and the fourth in R 453. The text below combines two notebooks that at first do not appear continuous, since R 448 ends on p. 48 and R 449 begins on p. 37. Careful analysis shows, however, that Peirce probably jumped from the near end of page 37 in R 448 to R 449; the transition is excellent, and weakens two other possibilities: that R 449 might have continued R 553 (which ends on a p. 37), or that R 449 follows a notebook that no longer exists. An important addendum—an answer to a listener’s question about the first lecture that Peirce provided at the beginning of his third lecture—has been printed in the notes.]
R 478. [The following text is the first section of “A Syllabus of Certain Topics of Logic,” a large document Peirce composed, mostly in October 1903, to supplement the Lowell Lectures “by some statements for which there will not be time during the lectures, and by some others not easily carried away from one hearing.” The syllabus contains six sections, of which the first three and the fifth are printed here (omitted are “Nomenclature and Divisions of Dyadic Relations” (R 539; CP 3.571–608) and “Existential Graphs: The Conventions” (R 508; CP 4.394–417). The Lowell Institute had only money to print a hundred copies of the first two and the sixth sections, which were distributed at the fourth lecture (printed by Alfred Mudge & Son, Boston, 1903). “An Outline Classification” (pp. 5–9 of the printed Syllabus) was published in CP 1.180–202.]
R 478. [This is the second section of the “Syllabus” (pp. 10–14 of the printed version); it was published in CP 2.219–226. Peirce discusses the ethics of terminology in a number of manuscripts. An earlier list of eight rules can be found at the beginning of R 434 (1902). In selection 24, the argument is central to Peirce’s coining of “pragmaticism.”]
R 478. [This is the third and longest section of the “Syllabus”; given its length, it was not printed in the pamphlet distributed to the audience. The subsection entitled “Speculative Grammar” was published in large part in CP 2.274–277, 2.283–284, 2.292–294, and 2.309–331.]
R 540. [This is the fifth section of the “Syllabus,” first published in CP 2.233–272. This is a document of the highest importance, since it is here that Peirce, for the first time, establishes the three sign trichotomies (one more than in the preceding selection: Qualisign, Sinsign, and Legisign are born here) and the ten classes of signs. In the summer of 1904, Hugo Münsterberg, at the time chairman of the Philosophy Department at Harvard, invited Peirce to submit one or two papers for the Congress of Arts and Sciences to be held in St. Louis in October of that year. Peirce answered on July 19, 1904, that he could not afford to go to St. Louis, but wanted to send two papers that some other person could read for him. The first one, “on logic,” was titled “Classification and Nomenclature for Triadic Relations.” No doubt Peirce had R 540, or a rewriting of it, in mind. Münsterberg replied that he could not accept papers not delivered by their authors, because they didn’t tend to generate enough interest.]
R 517. [First published in New Elements of Mathematics 4:235–263. Some time in 1904 Peirce set out to write a book on the foundations of mathematics, as appears from several related manuscripts variously titled “Dichotomic Mathematics” (R 4–5) or “Foundations of Mathematics” (R 7–11). Their content reveals a tight connection with R 517, which is a lengthy “Preface” (the document’s subtitle) to a book that intended to revisit the epistemic grounds of mathematics, following a rigorous, à la Euclid, methodology. As it turns out, “Καινὰ σ𝜏οιχει̑α” complements and supplements the third section of the “Syllabus,” “Sundry Logical Conceptions” (selection 20), very effectively.]
R 774. [First published by J. M. Krois in Philosophy and Rhetoric 11 (1978): 147–155. At the end of July 1904 Peirce published in the Nation a negative review of T. Clifford Allbutt’s Notes on the Composition of Scientific Papers. The book’s ineptitude set Peirce into thinking about the rhetoric of scientific communications (R 776), a topic about which he decided to write a two-part essay, the first part to be general, the other, special (R 777). Peirce apparently wrote only the first of the two papers, the complete title of which ends with the indication “No. 1.” A complete draft of R 774 is in R 775 (with the alternative title “Jottings on the Language of Science. No. 1”). It is unclear in which journal Peirce intended to publish the essay; it could have been the Popular Science Monthly, whose editor asked Peirce in September 1904 whether he could contribute an article—something Peirce had to forgo when he realized that the journal could not afford to pay him.]
P 1078: The Monist 15 (April 1905): 161–181. [Published in CP 5.411-437. In August 1904 Peirce told Carus he was writing a review of Herbert Nichols’s A Treatise on Cosmology and asked him whether he would take it for The Monist, given that Peirce wanted to use the occasion to defend his pragmatism. Carus agreed with some delay and Peirce continued his work, eventually deciding to split his article and publish the review and his considerations on pragmatism separately. He sent both papers to Carus in mid-September 1904, with the intention of having “What Pragmatism Is” followed by two supplementary papers, “The Consequences of Pragmaticism” and “The Evidences for Pragmaticism” (this plan for a sequel continued to evolve during the following two years). The last paragraph before the postscript of February 1905 was added by Peirce at the end of September 1904. The article appeared, with an unexplained delay, in the April 1905 issue, four months after the publication of the Nichols review. R 329 contains a copious draft of the combined review and essay.]
P 1080. The Monist 15 (October 1905): 481–99. [Published in CP 5.438-463. Soon after “What Pragmatism Is” appeared, Peirce received from various countries many letters of appreciation that encouraged him to pursue the discussion of pragmaticism in new articles (F. C. S. Schiller was one of the correspondents and he completely revised his opinion—until then negative and dismissive—of Peirce’s contribution to pragmatism). From the end of April to the end of June he worked on different versions of his second paper, all titled “The Consequences of Pragmaticism” (R 288, R 289, and R 1338 testify to this effort). The final draft is found in R 290, with the title changed to “Issues of Pragmaticism” as an afterthought. Paul Carus received the manuscript at the end of June and delayed its publication somewhat to make sure Peirce could see the proofs. Only the last 44 pages of the original manuscript are today extant in the Open Court archives preserved at Southern Illinois University in Carbondale (Special Collections, Morris Library), the first seventeen pages having disappeared. The document below reproduces pp. 481–486 of the Monist article, and then follows the manuscript, with appropriate emendations from the published article.]
R 908. [End of document published in CP 1.317–21. Peirce started working on a third paper for The Monist as soon as he finished “Issues of Pragmaticism.” He spent about nine months writing many versions of a text titled “The Basis of Pragmaticism.” The earliest version appears to be R 282 (a short discussion between “Jules” (also known as Giuliano el Sophista, or Giuseppe Prezzolini) and a “Respondent”). R 284 contains two thick notebooks forming an important working document, probably composed in September 1905. R 280 and R 281 were composed somewhat later in the fall, and the present document, which seems to follow them, was probably written in December 1905, thus preceding by a few days R 283 (the next chapter in this volume, dated January 1906). Peirce’s last attempt at writing “The Basis of Pragmaticism” is found in R 279, subtitled “Meditation the First” and dated March 1906. The editors have added the words “in Phaneroscopy” to the title of the present text so as to distinguish it from the next chapter. The full manuscript of this text consists of one page from R 282, then R 908 and R 1043 (the latter is a long note on chemical valency not published here). Peirce never published any of the “Basis” texts. He came to think that his existential graphs provided a more effective tool for proving pragmaticism, and he turned all his efforts to writing what became “Prolegomena to an Apology for Pragmaticism,” which The Monist did publish.]
R 283. [Published very partially in CP1.573-4, 5.448n, and 5.549-54. This document appears to have been composed mostly in January 1906. The editors have added “in the Normative Sciences” to the title to distinguish the text from the previous selection. R 283 is a bulky manuscript containing hundreds of draft and variant pages.]
R 318. [Not counting the many drafts of this document in R 317, R 319–322, all of which were planned as an article for The Nation and composed in February–March 1907, R 318 is in itself a highly complex and multi-layered manuscript, the first three versions of which were composed in March–April 1907. When Peirce realized that the Nation was not a suitable venue for such an ambitious article, he turned his hopes toward the better-paying Atlantic Monthly and produced two more versions some months later in 1907 (exactly when remains unclear for lack of textual clues). Indeed, the extant mass of manuscript sheets allows us to distinguish five intermingled versions of the article. They all share the same beginning (found in CP 5.11–13, 464–466). The Collected Papers published what appears to be the fourth version (5.467–481), followed by the second half of the second/third version (the latter two versions have a common trunk) in 5.481–496. A fragment of the fifth version was published in CP 1.560–562. Peirce signed each of the first three versions with his full name: Charles Santiago Sanders Peirce; the last two versions written somewhat later are unsigned. Published below are (1) the introduction common to all versions, (2) the third version, as “Variant 1,” and (3) the fifth version, as “Variant 2.” Peirce listed at some point the various topics addressed in an advanced earlier version of his article (R 322) in R 317.
Peirce was apparently prompted to write “Pragmatism” when in February 1907 he received a copy of the Florentine pragmatist journal Leonardo whose issue of that month carried a defining article by Giovanni Papini. But Peirce had probably been toiling with the idea for this paper since September 1906, in reaction to a remark made to him by Paul Carus about “pragmatist journals” (see R 323 and R 325). Neither Paul E. More, the new Nation editor, nor Bliss Perry, the Atlantic editor, accepted Peirce’s paper.] The Peirce Project‘s reconstruction and repagination of the entire R 318 folder in 1997 was many years later diagrammed by Priscila Borges in amazing fashion. The PDF enclosing that diagram is downloadable here.
R 841 and P1166: The Hibbert Journal, A Quarterly Review of Religion, Theology, and Philosophy 7 (October 1908): 90–112. [Cassius J. Keyser, a professor of mathematics at Columbia University and a member of the American editorial board of the Hibbert Journal, invited Peirce on April 8, 1908, to write an article for the journal on one of three topics. Peirce replied gratefully two days later, rejecting Keyser’s topics but suggesting ten other ones, the third of which was a “theological discussion”: “I should willingly treat a little known ‘proof’ of the Being of God. Properly speaking it is not itself a proof, but is a statement of what I believe to be a fact, which fact, if true, shows that a reasonable man by duly weighing certain great truths will inevitably be led to believe in God. . . .” Whether Keyser selected the third topic of Peirce’s list is not known, but Peirce probably had his mind already set since he started, the day after sending his ten suggestions, to jot down, in his “Prescott notebook” (R 277: 65–66, 11 April 1908), an outline of an article titled “A Little Known ‘Argument’ for the Being of God,” whose purpose was “to describe a way of gaining a rational and unshakable belief in God.” One month later Peirce finished, or rather stopped, composing the first version of his article, a 134-page document that began with a “dedication to a dream-friend” (R 842). He wrote to Keyser, on May 14, that he would be unable to finish his paper in time, having lost a week’s work, and that the paper required to be greatly condensed. In the course of the next six weeks Peirce then rewrote the article entirely, drafting and redrafting most of its pages several times (R 843 contains about 200 draft pages), and finally submitted his article toward the end of June (R 841). At the end of July Keyser let Peirce know that Lawrence Pearsall Jacks, the Hibbert editor, had accepted the article, finding it to be a contribution of “permanent value.” Jacks, however, because of the paper’s complexity, wanted Peirce “to summarize the article in a concluding page or two, to be added to the article, in order to forestall careless cavilers who might say, ‘what, then, precisely, is your neglected argument?’” Peirce accepted to write an addendum, which he called “Additament,” the first version of which is found in R 844 (CP 6:486–90). The Hibbert published, untitled, the second version (the original manuscript has not been recovered) after a blank line at the end of the article, to Peirce’s surprise: as he later explained to William James, he thought the additament was distasteful and he had asked the editor to pick out “a small passage that was neither egotistical nor offensive to anybody,” thinking that such an injunction would ensure “the rejection of the whole.’” Jacks, however, printed it entirely. It is apparent that Peirce got to proofread the main article but not the addendum. The text below reproduces R 841 with emendations from the published article, followed directly by the (here retitled) “Additament.”]
R 675. [In the spring of 1909, two friends of Victoria Lady Welby, J. W. Slaughter and G. F. Stout, decided to honor her by publishing a collection of essays on “Significs,” the main focus of her research. Peirce was glad to accept the invitation to contribute a chapter, which Lady Welby was especially anxious to see printed. Unfortunately, ill health and a host of other preoccupations prevented Peirce from completing his essay in due time, as a result of which the editors kept postponing the book’s publication. In April 1911 Slaughter sent Peirce a reminder. Peirce was at the time trying to write a book on “A Logical Criticism of Essential Articles of Religious Faith” (R 846–856), whose first part was to be on “logical critic.” Slaughter’s letter gave him a new impetus, and in early August he announced to Lady Welby that, although he wanted at first to write an abstract of his entire system of logic, constraints of space and time were forcing him to limit himself to “Logical Critics, that is, to the quality or grade of assurance that the three classes of reasoning afford.” R 669–670, titled “Assurance Through Reasoning,” may be part of an earlier effort. R 673–677, all titled “A Sketch of Logical Critic[s],” are Peirce’s different unsuccessful attempts to write the paper, probably in August 1911. R 675 is one of the more polished versions; as it was left unfinished, the last five sheets of the document are not printed here to give the text a better ending.]
R 682. [During the last two years of his life Peirce was very ill and could work only for a few hours on those rare days when he felt somewhat better. Among his last manuscripts we find a series of unfinished documents in which he attempted to continue his study of the assurance provided by the different types of reasoning. Noteworthy are R 680, “Analysis of the Trustworthiness of the Different Kinds of Reasonings,” and R 681, “A Study of How to Reason Safely and Efficiently.” The last adverb, “efficiently,” announces the appearance of a new theme, one that will receive a new name in the title of R 684: “A Study of Reasoning in its Security and in its Uberty.” “Uberty” is defined in the untitled R 683 (which may be an earlier—or later—variant of R 682) as the character “of being actually gravid with living and prolific truth.” The present selection was very probably composed in September–October 1913.]
L 463 and Welby Collection, York University. [Three important excerpts from Peirce’s correspondence to Lady Welby are published here; they shed a useful light on different aspects of his semiotic theory. The first excerpt comes from L463: 98–102, a letter draft composed in the early spring of 1906, and has been published in Charles Hardwick’s Semiotic and Significs: The Correspondence between Charles S. Peirce and Victoria Lady Welby pp. 196-197. The second excerpt comes from a letter dated 23 December 1908 (published in Semiotics and Significs pp. 80–85). The third excerpt comes from L463: 132–146, a letter-draft begun a few days before Christmas, 1908 (published in CP 8.342–376).]
L 224 and William James Papers, Houghton Library. [Peirce loved to write long and frequent letters on all manner of topics to his staunch friend and supporter William James. This part of the appendix includes excerpts of four letters composed in the course of 1909, the year preceding James’s death. The first excerpt comes from pp. 6–14 of an unsent draft Peirce began to write on 26 February 1909 (L 224: 90–98, published in CP 8.177–185 with some omissions, and in NEM III/2: 839–844). The letter became so large and unwieldy that Peirce sent James two other letters instead, one on March 9 and the other on March 14. The second excerpt comes from the latter document (pp. 6–10 of it, published in part in CP 8.314). The third excerpt consists of pp. 19–22 of a letter sent on 1 April 1909 (= CP 8.315). And the first eight pages of a letter begun on Christmas day, 1909, constitute the last extract (published in New Elements of Mathematics III/2: 867–71). All four documents provide useful precisions on semiotic and logical matters.]
In April 1887 Peirce moved with his second wife, Juliette,
from New York City to Milford, Pennsylvania, a small
resort town in the upper Poconos. A year and a half
later the Peirces moved into a farmhouse two miles
northeast of Milford in the direction of Port Jervis,
New York. This was to become Peirce’s Arisbe, named
for a Greek town south of the Hellespont, a colony
of Miletus, home of the first philosophers of Greece.
(1)
The renovation and expansion of the Arisbe house would
often preoccupy Peirce during his remaining years.
The architectural work of remodeling Arisbe, always
with an eye for something vast, would become a living
metaphor for his intellectual life.(2)
Starting in the mid-80s with his "Guess at the
Riddle," Peirce began to gather his philosophical
doctrines together into an integrated system of thought,
and with his 1891 Monist article, "Architecture
of Theories," he began to attend explicitly to
the structural integrity of his system as a whole.
One of Peirce’s main efforts after 1890 was to reestablish
pragmatism, not attended to since his 1877-78 "Illustrations,"
as an integral component of his systematic philosophy.
The integrating structure for his mature philosophy
would be a much expanded, though never fully completed,
theory of signs. Also prominent in Peirce’s later writings
is a more dominating form of naturalism that ties the
development of human reason unambiguously to natural
evolution and that takes on clear religious overtones.
The introduction printed in volume 1 (EP1) is the general
introduction for The Essential Peirce as a whole, but
no attempt was made to represent Peirce’s intellectual
development during his last two decades. This special
introduction to volume 2 (EP2) is intended to supplement
the general introduction by providing a sketch of this
period. Peirce’s life continues to resist easy characterization—unless
cryptically in the claim that he embodied the general
maxim he extolled in his fourth Harvard Lecture (sel.
13): "Never say die." There is no doubt that
his life was one of much suffering and many defeats,
but he never for long lost sight of his purpose: to
do what he could to advance human understanding. He
knew his own powers, and he knew the mundane truth
that knowledge is advanced through scholarly preparedness,
insight, humility, and hard intellectual work; and
it was no delusion of grandeur for him to realize that
he was poised to make contributions no one else could
make. The story of Peirce’s struggle to redeem his
talents is one of the great personal tragedies of our
time, but it cannot be told here.(3) These remarks are
intended only to provide a unifying structure for the
writings in this collection and a vantage point for
surveying the grand expanse of a remarkably rich and
complicated mind.
One obstacle to a comprehensive understanding of Peirce’s
thought is the broad range of his intellectual achievements,
covering so many of the human and physical sciences;
but added to that is the difficulty of determining
to what extent he was influenced by his predecessors
and peers. Of course, no one can think in a vacuum—thought
must necessarily relate to past thought, just as it
must appeal to subsequent thought—so it is never cogent
to ask about any thinker whether his or her thought
was influenced by previous thinkers, but only how and
to what extent. To Peirce, this was obvious. Given
his upbringing among mathematicians and experimental
scientists he learned early that intellectual progress
is always relative to knowledge already gained and
that any successful science must be a cooperative endeavor.
One of the reasons Peirce is so important for the history
of ideas is that he approached philosophy in this way,
knowing that if philosophy was ever really to amount
to anything it would have to abandon the notion that
great ideas arise ex nihilo—that one's ideas are wholly
one's own. As a result of this understanding, and of
his desire to help move philosophy toward a more mature
stage of development, Peirce became a diligent student
of the history of ideas and sought to connect his thought
with the intellectual currents of the past. He also
studied carefully the leading ideas of his own time.
His debts are extensive—far too numerous to be cataloged
fully here—but it could not be too far wrong to say
that Aristotle and Kant were his most influential predecessors,
with Plato, Scotus, and perhaps Berkeley coming next,
although only on the heels of many others such as Leibniz,
Hegel, and Comte. With respect to Peirce’s scientific,
mathematical, or logical ideas, others have to be added,
including, certainly, De Morgan and Boole. When one
considers how Peirce’s thought was influenced by the
ideas of his contemporaries one is hard-pressed to
settle on a short list. Peirce was very current in
many fields of study, due both to his scientifically
informed approach and to the fact that he wrote hundreds
of book reviews and newspaper reports on scientific
meetings and "picked up" ideas along the
way. In logic and mathematics, and even in philosophy,
aside from predecessors, the influence of Cayley, Sylvester,
Schröder, Kempe, Klein, and especially Cantor
stands out. Peirce was also responsive to the writings
of his fellow-pragmatists, among whom he included Josiah
Royce; but he was more influenced by William James
than by any other contemporary. Other contemporaries
of note were the philosopher and editor, Paul Carus,
and the English semiotician, Victoria Lady Welby, whose
work on signs ("significs") led her to Peirce,
and whose attentive interest in his semiotic ideas
encouraged him to develop his theory of signs more
fully than he would have without her.
Paul Carus (1852-1919) is a special case. Carus, a student
of Hermann Grassmann, has been surprisingly neglected
by historians, given his remarkable output as a philosopher
and his importance as an editor and critic. He wrote
scores of books and hundreds of articles (not only
on philosophy) and edited over one hundred issues of
the Monist and over seven hundred issues of the Open
Court, the two periodical publications of the Open
Court Publishing Company.(4)
Open Court authors included
the classic American quartet, Peirce, James, Royce,
and Dewey, and a host of others ranging from Ernst
Mach and Bertrand Russell to D. T. Suzuki. Carus was
a confirmed monist, as is revealed in the name of his
journal, and devoted to the reconciliation of science
and religion. He took a special interest in Peirce
and for over twenty years, notwithstanding some periods
of acrimony, he did more to promote Peirce’s philosophy
than anyone. Beginning in 1891, Carus published nineteen
of Peirce’s articles (thirteen in The Monist and six
in The Open Court) and many of Peirce’s unpublished
writings were intended for Carus. The important role
played by Carus in Peirce’s later life, in particular
the fact that after 1890 Peirce wrote most of his best
work for the Monist, is what led Max Fisch to call
that time Peirce’s Monist period.
The writings in the present volume begin in 1893 when
Peirce was fifty-four years old, only three years into
the Monist period and one year after his forced resignation
from the Coast and Geodetic Survey. He had recently
delivered a course of lectures on "The History
of Science" at the Lowell Institute in Cambridge
and was just bringing to a close—one article prematurely—his
influential metaphysical series for the Monist (EP1,
sels. 21-25). He was at work on "Search for a
Method," which was to include a substantially
revised version of his 1877-78 "Illustrations
of the Logic of Science" (EP1, sels. 7-12), and
was about to announce a twelve-volume opus, The Principles
of Philosophy, possibly inspired by James's recent
success with his Principles of Psychology. Clearly,
the opening writings of the present volume arose in
the context of an active and ongoing program of research.
For an intellectual profile of EP2, the separate headnotes
to the selections might be read consecutively. Although
they were not composed to provide a continuous flow
of text, they do give an idea of a thread of intellectual
development that ties together the writings in this
volume. Obviously it is not possible to capture rich
full texts, as most of Peirce’s are, in short notes,
but sometimes a single strand of connected meaning
is all that is needed to precipitate more substantial
linkings. Building on the headnotes, bearing in mind
some of the biographical structures developed in the
general introduction in EP1, and also some of the more
significant intellectual events of this later period,
the following sketch emerges as one way to trace Peirce’s
development.
In the first selection, "Immortality in the Light
of Synechism," written in 1893, Peirce gave an
indication of the significance of the argument for
continuity that he had planned for a conclusion to
his Monist metaphysical series. "I carry the doctrine
so far as to maintain that continuity governs the whole
domain of experience in every element of it. Accordingly,
every proposition, except so far as it relates to an
unattainable limit of experience (which I call the
Absolute), is to be taken with an indefinite qualification;
for a proposition which has no relation whatever to
experience is devoid of all meaning." Synechism
would guide Peirce’s philosophical investigations for
the rest of his life. Peirce also signaled his growing
conviction that science and religion were closely allied
at some deep level.
The following year, in "What is a Sign?" (sel.
2), Peirce explored the relationship between logic
and semiotics—even equating reasoning with semiosis.
"What is a Sign" is taken from Peirce’s unpublished
book "How to Reason," also known as "Grand
Logic." Elsewhere in that work, Peirce revived
the nominalism-realism issue, which he had not dealt
with since 1871, and he identified himself, for the
first time, as an "extreme" realist.(5)
Another year later, in "Of Reasoning in General"
(sel. 3), he further developed his semiotic theory
of logic elaborating more fully his theory that propositions
must always involve two signs, one iconic and the other
indexical. These ideas, along with the idea that our
success in discovering natural laws is explained by
our affinity with nature, would reemerge as key conceptions
in Peirce’s struggle to rework pragmatism and to account
for non-rational human insight. But for a time, he
would submerge himself in writing a mathematical textbook
called "New Elements of Mathematics,"(6) and
also in formal logic, particularly in some elaborate
reviews of the recently published volumes of Ernst
Schröder's Vorlesungen über die Algebra der
Logik.(7)
Near the end of 1896 Peirce took what Max Fisch calls
his "most decisive single step" in his progress
toward an all-encompassing realism: he accepted "the
possible" as a "positive universe" and
rejected the nominalist view that the possible is merely
what we do not know not to be true.(8) Peirce reported
this change of mind in January 1897 in his second Schröder
review (CP 3.527) and on 18 March wrote to James that
he had "reached this truth by studying the question
of possible grades of multitude, where I found myself
arrested until I could form a whole logic of possibility"
(CP 8.308). With his acceptance of real possibilities—which
put Peirce in the Aristotelian wing of the realist
camp—Peirce had become what Fisch called "a three-category
realist," no longer regarding the potential as
what the actual makes it to be, and now distinguishing
the generality of firsts from the generality of thirds.
Peirce’s embrace of what he would come to call "would-be's"
marks a watershed that might be said to separate his
middle years from the final period of his intellectual
life. This change, in conjunction with his attention
to the importance of continuity, would motivate much
of the content of his 1898 Cambridge Conferences Lectures.
However, the two lectures from that set that are included
in the present volume (sels. 4 and 5) were perhaps
shaped more by another event: the 1897 appearance of
William James's book, The Will to Believe and Other
Essays in Popular Philosophy. James had dedicated that
book "To my old friend, Charles Sanders Peirce,
to whose philosophic comradeship in old times and to
whose writings in more recent years I owe more incitement
and help than I can express or repay." Peirce
was touched, and on 13 March wrote a reflective letter
to James expressing his appreciation ("it was
a truly sweet thing, my dear William"), and pointing
out some ways his thinking had been affected by his
experience of "the world of misery" which
had been disclosed to him. Although rating "higher
than ever the individual deed as the only real meaning
there is [in] the Concept," he had come to see
"more sharply than ever that it is not the mere
arbitrary force in the deed but the life it gives to
the idea that is valuable." It is not to "mere
action as brute exercise of strength" that we
should look if we want to find purpose. Peirce praised
James's opening essay, "The Will to Believe,"
especially for its style and lucidity, but he clearly
had reservations. James introduced his essay as an
illustration of the continuing concern at Harvard for
"vital subjects": it is "a defence of
our right to adopt a believing attitude in religious
matters, in spite of the fact that our merely logical
intellect may not have been coerced."(9) A key point
is that "our non-intellectual nature" influences
our convictions. "Our passional nature,"
James wrote, "not only lawfully may, but must,
decide an option between propositions, whenever it
is a genuine option that cannot by its nature be decided
on intellectual grounds." It seems evident that
in his Cambridge Conferences Lectures Peirce’s great
interest in the tensions between theory and practice,
and his advocacy of "the will to learn" as
a prerequisite to actually learning, were stimulated
by James's "The Will to Believe." It is noteworthy
that from at least that time on, the role of instinct,
or sentiment, as a co-participant with reason in the
acquisition of knowledge became a key concern for Peirce,
and it would not be long until he came to regard ethics
and esthetics as epistemically more fundamental than
logic.
Less than six months after hearing Peirce’s lectures
in 1898, William James traveled to California to address
(on 26 August) the Philosophical Union at Berkeley.(10)
It was in that lecture, entitled "Philosophical
Conceptions and Practical Results," that James
publicly introduced the word "Pragmatism."(11)
James told his auditors that he would have preferred
the name "Practicalism" but that he had settled
on "Pragmatism" because that was the name
Peirce had used in the early 1870s when he first advocated
for pragmatism before the Cambridge Metaphysical Club.(12)
James was by this time one of America's most respected
intellectuals and his message fell on fertile ground;
before long there were a host of pragmatists in the
U.S. and abroad. James's acknowledgment of Peirce as
the originator of pragmatism increased Peirce’s prominence
and opened for him an opportunity to bring his distinct
views into the growing international debate.(13)
Peirce’s second wave of interest in pragmatism is often
thought to have started with James's California lecture,
but it would be more accurate to say that it began
in the early 1890s with the resumption of his research
in logic and methodology for his "Critic of Arguments"
series for the Open Court, and for his books, "Search
for a Method" and "How to Reason." If
anything, James's 1890 Principles of Psychology, especially
the treatment of the role of inference in perception,
probably had more to do with Peirce’s return to pragmatism.
But it was also about 1890 when Peirce accepted the
reality of actuality, or secondness, and then saw clearly
that the individual is to be distinguished from the
general. It may have been the logical ramifications
of that large step toward a more embracing realism,
precipitated by his recognition in the mid-80s of the
need for both icons and indices for meaningful reference,
that led Peirce to begin to rethink the argument of
his 1877-78 "Illustrations." Nevertheless,
it surely was the increasing popularity of pragmatism
that James had spawned in 1898 that led Peirce to resolve
to produce a proof that would distinguish his version
of pragmatism from popular versions and sanction his
as the "scientific" one.
The nineteenth century, after his Cambridge Conferences
Lectures, came to a bad ending for Peirce. Between
periods of illness and failures to land employment
Peirce must have learned more about misery.(14) But he
continued to make intellectual progress. On 17 August
1899 he wrote to Carus that "the true nature of
continuity . . . is now quite clear to me." Previously
Peirce had been "dominated by Cantor's point of
view" and had dismissed Kant's definition unjustly.
Now he saw that it is best not to try "to build
up a continuum from points as Cantor does."(15)
He began the twentieth century thinking about great
men of science. On 12 January 1901 he published "The
Century's Great Men in Science" in the New York
Evening Post, noting that "the glory of the nineteenth
century has been its science" and asking what
it was that has distinguished its great contributors.(16)
"Their distinctive characteristic throughout the
century, and more and more so in each succeeding generation,
has been devotion to the pursuit of truth for truth's
sake." He reflected on his own boyhood in Cambridge
and on the leaders of the "scientific generation
of Darwin," most of whom had passed through his
home: "The word science was one often in those
men's mouths, and I am quite sure they did not mean
by it 'systematized knowledge,' as former ages had
defined it, nor anything set down in a book, but, on
the contrary, a mode of life; not knowledge, but the
devoted, well-considered life-pursuit of knowledge;
devotion to Truth—not 'devotion to truth as one sees
it,' for that is no devotion to truth at all, but only
to party—no, far from that, devotion to the truth that
the man is not yet able to see but is striving to obtain."
As Peirce’s career opportunities dried up he came more
and more to regard science and philosophy as devout
pursuits.
Fortunately for Peirce, near the end of 1900 James Mark
Baldwin hired him to finish the logic definitions after
"J" for his Dictionary of Philosophy and
Psychology. This work occupied much of Peirce’s time
in 1901, yet he managed to publish about twenty book
reviews and to translate seven articles for the Smithsonian.
One of the books Peirce reviewed in 1901 was Karl Pearson's
Grammar of Science (sel. 6). An idea Peirce had put
forward in his Cambridge Conferences Lectures, that
it is illogical to make one's personal well-being "a
matter of overwhelming moment," can be seen to
be at work in this review. Peirce objected to Pearson's
claim that human conduct should be regulated by Darwinian
theory and that social stability is the sole justification
of scientific research. The human affinity with nature
that Peirce had earlier appealed to to explain our
success in discovering natural laws (sel. 3), was here
explained as resulting from the fact that the human
intellect is an outgrowth of the rationality inherent
in nature. This was a further rejection of nominalism,
which holds that the rationality in nature arises in
human reason. Peirce also rejected Pearson's claim
that there are first impressions of sense that serve
as the starting point for reasoning, and argues that
reasoning begins in percepts, which are products of
psychical operations involving three kinds of elements:
qualities of feelings, reactions, and generalizing
elements.
In 1901 in "Laws of Nature" (sel. 7), Peirce
reviewed different conceptions of natural law and argued
that the typical conception of scientists is that a
law of nature is an objective fact—"much more
reliable than any single observation." In remarking
on the method scientists employ in their "exhumation"
of laws of nature, he briefly described a method of
conjecture and testing that he would develop in the
following selection, "On the Logic of Drawing
History from Ancient Documents." In selection
8, Peirce gave one of his most elaborate accounts of
the different kinds of reasoning. He drew a distinction
between two kinds of deductive reasoning, corollarial,
which draws only those conclusions that can be derived
from the analysis and manipulation of the premisses
as given, and theorematic, which enriches the inference
base by adding propositions which were not part of
the original premiss set—and "which the thesis
of the theorem does not contemplate" (p. 96).
Peirce believed this distinction to be the most important
division of deductions, and his most important discovery
in the logic of mathematics.(17) He also introduced the
crucial point he would elaborate in his 1903 Harvard
Lectures that "logical criticism cannot go behind
perceptual facts"—the "first judgments which
we make concerning percepts." Logic cannot criticize
involuntary processes. Yet these "first judgments"
do represent their percepts, although "in a very
meager way."
By mid-1901 Peirce was ready to draw together the many
interesting and diverse results he had been achieving
into a major book project. The book was to be on logic,
but in addition to reflecting his findings on continuity
and modality, and his excitement with his progress
on a graphical syntax for formal logic, he would incorporate
his new discoveries in semiotics and reflect his growing
belief that logic is a normative science. The book
would be called "Minute Logic" to reflect
the minute thoroughness with which he planned to examine
every relevant problem. An early draft of the first
chapter (MS 425) began with a section entitled "Logic's
Promises" and the opening sentence: "Begin,
if you will, by calling logic the theory of the conditions
which determine reasonings to be secure." Within
a year Peirce had drafted and redrafted hundreds of
pages, and had finished four large chapters.(18) In July
1902 he prepared an elaborate application asking the
Carnegie Institution, presided over by Daniel C. Gilman,
to fund his "Logic" which he had reconceived
as a set of thirty-six memoirs. His application ran
to forty-five pages in typescript, and remains the
best single guide to Peirce’s system of thought.(19)
Even though Peirce received strong recommendations
from a powerful group of supporters, including the
President, Theodore Roosevelt, and Andrew Carnegie
himself, his project was not funded. On 19 June 1903
Peirce’s brother, James Mills (Jem) wrote to William
James: "Nobody who is familiar with the history
of this affair can doubt that the refusal of the Committee
is due to determined personal hostility on the part
of certain members of the Committee." The matter
had dragged on for so long, though, that by the time
the rejection was definite, Peirce had already given
his 1903 Harvard Lectures and was preparing for his
Lowell Institute series—he would never return to his
"Minute Logic." Jem wrote to James again
on 23 June about the injustice of the Carnegie decision
and thanked James for securing the Harvard Lectures
for Charles: "I consider that the set of lectures
given this Spring at Cambridge and the promise of the
Lowell Lectures have saved him from going to ruin.
For his fortunes were so desperate, that he could not
much longer have resisted forces tending to destroy
his bodily health and break down his mind."
The part of the "Minute Logic" included in
EP2 is an excerpt from a chapter on the classification
of the sciences. In "On Science and Natural Classes"
(sel. 9), Peirce described a "natural class"
as one "whose members are the sole offspring and
vehicles of one idea," and he explained how ideas
can "confer existence upon the individual members
of the class"—not by bringing them into material
existence, but by conferring on them "the power
of working out results in this world." Such ideas,
Peirce says, when not embodied have a "potential
being, a being in futuro." This is Peirce’s account
of final causation, the power that ideas have "of
finding or creating their vehicles, and having found
them, of conferring upon them the ability to transform
the face of the earth." Such is the power, Peirce
believes, of the ideas of Truth and Right. It is in
this context that he quotes the famous line from William
Cullen Bryant, "Truth, crushed to earth, shall
rise again."
In following out this thread of connecting ideas we
come to what is probably the single most significant
time in Peirce’s mature life of ideas, his time in
Cambridge in 1903 when he gave his famous "Harvard
Lectures," just referred to above, followed not
long after by his third series of Lowell Lectures.
Peirce had paid close attention to the stream of writings
on pragmatism that was gaining momentum and he thought
the time had come for him to make a case for a more
or less definitive core statement. But making his case
or, as he saw it, proving his thesis, was a complicated
matter requiring the marshaling of support from all
areas of his vast system of thought. Further complicating
matters was the fact that Peirce’s system had gone
through many changes since the 1870s. Among the more
significant of those changes, some already mentioned
above, was his acceptance of the reality of actuality
(secondness) and later of possibility (firstness);
his realization that human rationality is continuous
with an immanent rationality in the natural cosmos;
and his new-found conviction that logic is a normative
science, epistemically dependent on ethics and esthetics.
For Peirce, pragmatism had become a doctrine that conceptions
are fundamentally relative to aims rather than to action
per se as he had held in earlier years. To prove pragmatism,
then, called for a basic rethinking within the context
of a transformed, and still growing, philosophy. That
was the task Peirce set out to perform in his 1903
Harvard and Lowell Lectures, and the program he inaugurated
that year would guide him for the rest of his life.
In his Harvard Lectures, Peirce built his case for pragmatism
on a new theory of perception, grounded in his theory
of categories and on results from phenomenology, esthetics,
and ethics (sel. 10). He argued that there is a realm
of reality associated with each category and that the
reality of thirdness is necessary to explain a mode
of influence on external facts that cannot be explained
by mechanical action alone (sel. 11). He argued that
pragmatism is a logical, or semiotic, thesis concerning
the meaning of a particular kind of symbol, the proposition,
and explained that propositions are signs that must
refer to their objects in two ways: indexically, by
means of subjects, and iconically, by means of predicates
(sel. 12). The crucial element of Peirce’s argument,
from the standpoint of his realism, involved the connection
between propositional thought and perception. To preserve
his realism, Peirce distinguished percepts, which are
not propositional, from perceptual judgments, which
are propositional, and which are, furthermore, the
"first premisses" of all our reasonings.
The process by which perceptual judgments arise from
percepts became a key factor in Peirce’s case (sel.
13). But if perceptual judgments are the starting points
for all intellectual development, then we must be able
to perceive generality (sel. 14). Peirce next argued
that abduction shades into perception, so that pragmatism
may be regarded as the logic of abduction, and, finally,
isolated three key points: that nothing is in the intellect
that is not first in the senses; that perceptual judgments
contain general elements; and that abductive inference
shades into perceptual judgment without any sharp line
of demarcation (sel. 15). Pragmatism, Peirce showed,
follows from these propositions (sel. 16).
According to Fisch,(20)
it was in the Harvard Lectures
that Peirce, for the first time, made it clear that
his realism was opposed to idealism as well as to nominalism.
Peirce’s new theory of perception embraced the doctrine
of immediate perception, to deny which, according to
Peirce, "cuts off all possibility of ever cognizing
a relation." That idea was carried forward into
the Lowell Lectures, where Peirce continued with his
effort to prove pragmatism, making his best attempt
so far, according to Fisch.(21) In "What Makes a
Reasoning Sound" (sel. 17), the only lecture from
the Lowell series that is included in EP2, Peirce made
a strong case for objective grounds for evaluating
reasonings and argued that with the right method even
"a slight tendency to guess correctly" will
assure progress toward the truth.
In conjunction with his Lowell Lectures, Peirce prepared
a "Syllabus" to be distributed to his auditors.
The first part is "An Outline Classification of
the Sciences" (sel. 18), showing the normative
sciences—esthetics, ethics, and logic—as constituting
the central part of philosophy, and giving the order
of epistemic and data—support relationships among the
sciences that will guide his subsequent research. In
"The Ethics of Terminology" (sel. 19), Peirce
paused from his central task to elaborate on an issue
that had been troubling him since he began working
on logic entries in 1900 for Baldwin's Dictionary (and
perhaps earlier with his work for the Century Dictionary):
the unscientific terminology that prevailed in philosophy.
Peirce recognized that philosophy could never abandon
ordinary language altogether, for it is essential to
understanding common conceptions, but philosophical
analysis and progress calls for a specialized vocabulary.
That was Peirce’s strong conviction, and it explains
his frequent resort to neologisms.
It may be that the attention Peirce gave to his classification
of the sciences, along with his new-found conviction
that logic is coextensive with semiotics, provided
the impetus for the remaining two parts of the "Syllabus"
that are included in EP2. They introduced a shift to
an intensive development of his theory of signs along
taxonomic lines motivated by his categories. In "Sundry
Logical Conceptions" (sel. 20), Peirce introduced
the semiotic trichotomy that divides signs according
to whether they are interpreted as signs of possibility,
fact, or law: rhemes (here called sumisigns), dicisigns,
and arguments. That trichotomy was additional to his
long-held division of signs according to whether they
represent their objects by virtue of similarity, existential
connection, or law: icons, indices, or symbols. In
"Nomenclature and Divisions of Triadic Relations"
(sel. 21), Peirce introduced another trichotomy that
distinguishes signs according to whether, in and of
themselves, they are qualities, existents, or laws:
qualisigns, sinsigns, and legisigns. With these three
trichotomies in place, Peirce was able to identify
ten distinct classes of signs. This was the beginning
of a rapid development of his formal semiotic theory.
There were two other parts of the "Syllabus"
that are not included in EP2, one on Peirce’s system
of Existential Graphs, which Peirce would later choose
as the preferred medium for the presentation of his
proof of pragmatism, and the other an in-depth treatment
of dyadic relations parallel to the treatment of triadic
relations found in selection 21.
In the next two selections Peirce shifted his attention
from pragmatism and its proof to concentrate more fully
on the theory of signs. In "New Elements"
(sel. 22), he focused on the abstract mathematical
structures necessarily exhibited by sign relations
and argued, as he had in "On Science and Natural
Classes," that "representations have power
to cause real facts" and that "there can
be no reality which has not the life of a symbol."
And in "Ideas, Stray or Stolen, about Scientific
Writing" (sel. 23) Peirce gave one of his most
focused accounts of speculative rhetoric, the third
branch of his semiotic trivium, which has as its aim
to find out "the general secret of rendering signs
effective." Peirce made it clear that the range
of legitimate semiotic effects (interpretants) includes
feelings and physical results, as well as thoughts
and other signs. Peirce reiterated a point he had made
at least as early as his Harvard Lectures, that nothing
can be represented unless it is of the nature of a
sign, and he stressed that ideas can only be communicated
through their physical effects.
While Peirce was writing about semiotics—and topics
outside the scope of this volume (e.g., mathematics
and graphical logic)—he had not stopped thinking about
pragmatism. On 7 March 1904 he wrote to William James:
"The humanistic element of pragmatism is very
true and important and impressive; but I do not think
that the doctrine can be proved in that way. The present
generation likes to skip proofs. . . . You and Schiller
carry pragmatism too far for me. I don't want to exaggerate
it but keep it within the bounds to which the evidences
of it are limited." By this time he was already
at work on the first article of another series of papers
for the Monist where he would again take up the proof
of pragmatism.
Peirce’s third Monist series opened with the April 1905
publication of "What Pragmatism Is" (sel.
24). This was to be the first of three papers that
would explain in detail Peirce’s special brand of pragmatism,
give examples of its application, and prove it. Not
long into his paper, Peirce paused to deliver a short
lesson on philosophical nomenclature—the message being
essentially the same as that of selection 19—as a rationale
for renaming his form of pragmatism. He chose the name
"pragmaticism" as one "ugly enough"
to be safe from kidnappers. Peirce lamented that his
word "pragmatism" was now met with in the
literary journals, "where it gets abused in the
merciless way that words have to expect when they fall
into literary clutches." He would continue using
his new "ugly" word for the rest of the Monist
series, and as late at 1909 (sel. 30, p. 457) he used
"pragmaticism" because, he wrote, James and
Schiller had made "pragmatism" imply "the
will to believe, the mutability of truth, the soundness
of Zeno's refutation of motion, and pluralism generally";
but he would often revert to his original name, indicating
that he may not really have wanted to give it up.
After his excursus into philosophical terminology, Peirce
examined the presuppositions of pragmaticism with his
proof in mind. One key assumption was that all mental
development (learning) takes place in the context of
a mass of already formed conceptions, and another was
that meaning is always virtual. He also argued for
the relevance of all three of the categories of being
for his pragmaticism: thought (thirdness) can only
govern through action (secondness) which, in turn,
cannot arise except in feeling (firstness).
The same year, in "Issues of Pragmaticism"
(sel. 25), Peirce restated his pragmatic maxim in semiotic
terms, along lines suggested in his sixth Harvard Lecture
(sel. 15). He identified the meaning that pragmaticism
seeks to enunciate as that of symbols rather than of
simple conceptions. The thrust of this article was
to articulate his forms of critical common-sensism
and scholastic realism, which he regarded as consequences
(or "issues") of pragmaticism. He extended
his realism to include the acceptance of "real
vagues" and "real possibilities," and
he pointed out that "it is the reality of some
possibilities that pragmaticism is most concerned to
insist upon." According to Fisch, pragmaticism
had now become pragmatism "purged of the nominalistic
dross of its original exposition."(22)
There are a number of manuscript drafts for a third
Monist article which indicate that Peirce intended
to proceed with his proof along lines he would follow
in selection 28. In one of those drafts, "The
Basis of Pragmaticism in Phaneroscopy" (sel. 26),
he began with an argument from the valency of concepts
based in his phenomenology (phaneroscopy) and theory
of categories. In another, "The Basis of Pragmaticism
in the Normative Sciences" (sel. 27), he focused
on the normative sciences, especially on his general
theory of signs, as the key to the proof. Peirce pointed
out that the pragmaticist will grant that the "summum
bonum" consists in a "continual increase
of the embodiment of the idea-potentiality" but
insisted that without embodiment in something other
than symbols, "the principles of logic show there
never could be the least growth in idea-potentiality."
Around this time, Peirce was working intensely on the
formal structure and systematic interconnections of
semiotic relations. His logic notebook (MS 339) in
1905 and 1906 is rife with semiotic analyses and discoveries
giving weight to the idea that it was in the context
of his theory of signs that he expected to deliver
his promised proof of pragmaticism. But when the third
article of the series, "Prolegomena to an Apology
for Pragmaticism," finally appeared in October
1906, it turned out to be an explication of his system
of logical graphs, the Existential Graphs, instead
of the expected proof. Peirce had decided that it was
by means of the Existential Graphs that he could most
convincingly set out his proof, which was to follow
in subsequent articles (although it is significantly
previewed in this one). Peirce had decided to use his
system of graphs for his proof for three principal
reasons: it employed the fewest possible arbitrary
conventions for representing propositions, its syntax
was iconic, and it facilitated the most complete analysis.
Peirce worked for years on the continuation of this
series, but he never finished it.
It is not known for certain why Peirce was unable to
complete his Existential Graphs-based proof, but it
is often supposed to have been a consequence of his
failure to reach a satisfactory solution to the problem
of continuity.(23) It is clear that Peirce expected his
argument for pragmatism to also constitute a proof
of synechism (see selection 24, p. 335). So it may
have been technical problems involving the logic of
continuity that kept Peirce from completing this series
of papers. Peirce interrupted his efforts to complete
this third Monist series with a separate series on
"amazing mazes" (two articles of a proposed
three were published in 1908-9) in which he developed
applications of the Existential Graphs and worked out
new definitions of continuity.(24) This mathematical
line of thought led Peirce into a number of important
technical questions involving probability and modality.
By February 1909, Peirce had worked out a matrix method
for an extension of the propositional calculus to three
values—at least ten years before the similar work of
Lukasiewicz and Post.(25) Peirce’s acceptance of real
possibility had convinced him that the definition of
"probability" should include reference to
dispositions in addition to frequencies, but even though
he tried many alternatives involving the propensity
view he was never satisfied that he had got it quite
right.(26) For Peirce, this was a matter of considerable
importance for pragmatism, because one of the great
defects he found with his early theory was the nominalistic
appeal to a frequency theory of probability. He also
gave up the material interpretation of logical implication.(27)
Among the more entangled and confounding sets of manuscripts
in the Harvard collection (the manuscripts acquired
by the Harvard Philosophy Department after Peirce’s
death) is one from 1906-7 in which Peirce attempted
to compose a more or less popular account of pragmaticism—but
again called "pragmatism"—and to give at
least a summary proof (MSS 316-22). Nominally, Peirce
was composing a "letter to the editor," initially
for the Nation but later for the Atlantic, although
Peirce recognized it as a full-fledged article in his
correspondence. In the two variants combined in selection
28, Peirce delivered a proof that is probably the one
he was intending to give in the Monist before he decided
on a more formal approach using his Existential Graphs.
The proof in selection 28 is based on Peirce’s theory
of signs, beginning with the premiss that every concept
and every thought beyond immediate perception is a
sign, and concluding with the proposition that a final
logical interpretant must be of the nature of a habit.
This selection provides an illuminating integration
of Peirce’s theory of signs, including his mature theories
of propositions and inference, with his pragmaticism.
It is evident from the refinement of the theory of signs
expressed in his remarkable "letter" that
Peirce had not given up work on semiotics when he turned
to his Existential Graphs for his Monist proof of pragmatism.
There may have been a hiatus following his failure
to get his "letter" into print, but by August
1908 he was hard at work on the classification of triadic
relations (MS 339) and in December he resumed discussion
of his theory of signs in correspondence with Lady
Welby (sel. 32). Peirce’s letters to Lady Welby record,
often in summary form, the most advanced theory of
signs ever fashioned. The theory as a whole is far
too complex to be represented here, although it was
lightly sketched in the general introduction in EP1,
and a recent book by James Liszka provides an excellent
introduction to the system in full.(28) For the thread
of intellectual development being pursued here, it
is noteworthy that early in 1906 Peirce wrote to Lady
Welby that he had found it necessary to distinguish
two semiotic objects (immediate and dynamical) and
three interpretants (here called "intentional,"
"effectual," and "communicational"),
and he introduced the important conception of the commens,
which "consists of all that is, and must be, well
understood between utterer and interpreter, at the
outset, in order that the sign in question should fulfill
its function." On 23 December 1908 Peirce defined
"sign" as "anything which is so determined
by something else, called its Object, and so determines
an effect upon a person, which effect I call its Interpretant,
that the latter is thereby mediately determined by
the former." He immediately added that the only
reason he had inserted "upon a person" into
his definition was because he despaired of making his
broader conception understood. Over the course of the
next few days he laid out his "ten main trichotomies
of signs" (eight of them had been quietly given
in a single remarkable paragraph on pp. 402-3 of selection
28), the tenth one being the division that expresses
the three sources of assurance utterances can have:
instinct, experience, or form. This tenth trichotomy
would occupy Peirce a great deal during his remaining
five years. Peirce’s correspondence with William James
(sel. 33) repeats many of the same semiotic developments
recorded in the letters to Lady Welby, but sometimes
more perspicuously and always in a different voice.
Modal considerations are more evident in the letters
to James. As pointed out above, by 1909 Peirce had
made deep advances into modal logic and this is reflected
in various ways; for example, in Peirce’s emphatic
statement that the final interpretant consists in the
way every mind "would act," not in the way
any mind does act, and also in Peirce’s division of
semiotic objects into may-be's, actualities, and would-be's.
On 9 April 1908 Peirce received a letter from Cassius
J. Keyser inviting him to write an article for the
Hibbert Journal. Peirce replied (10 April), outlining
ten alternative topics and asking Keyser to choose
one. Peirce had written, as his third alternative:
"as I believe the Hibbert Journal is favorable
to theological discussion, I should willingly treat
a little known 'proof' of the Being of God. Properly
speaking it is not itself a proof, but is a statement
of what I believe to be a fact, which fact, if true,
shows that a reasonable man by duly weighing certain
great truths will inevitably be led to believe in God."(29)
Whether it was Keyser or Peirce who chose the third
alternative is not clear, but Peirce spent most of
the next three months composing "A Neglected Argument
for the Reality of God" (sel. 29).
In that paper Peirce examined the attractive force of
the idea of God and concluded that humans instinctively
gravitate to it. He contended that belief in God is
irresistible to anyone who naturally (through musement)
comes to contemplate the possibility of God. The "God
hypothesis" appears to be a special kind of abduction
(he uses "retroduction" instead of "abduction"
in this paper). It arises from a human power of guessing
that is analogous to the instincts of animals, and
because it recommends itself with unusual force we
can take "a certain altogether peculiar confidence"
in it as a sign of the truth. Peirce called this his
"humble argument" but pointed out that it
is not a "proof" because the process leading
from the idea of God to belief in God is not a reasoned
(self-controlled) development of ideas. Peirce was
led to make a distinction between "argument"
and "argumentation" that he had not explicitly
made before: an argument is "any process of thought
reasonably tending to produce a definite belief"
while an argumentation is "an argument proceeding
upon definitely formulated premisses." An argument,
in other words, does not have to be self-controlled.
The power of guessing was put forward as "a sort
of divinatory power," what Galileo called il lume
naturale, and appears to have supplanted Ockham's razor
in Peirce’s methodological arsenal.
As the conclusion of an "argumentation," the
"God hypothesis" must pass through the three
successive stages of inquiry: retroduction, deduction,
and induction. Peirce devoted nearly half the paper
to a discussion of these three stages, but ended up
giving only the barest sketch of how they apply in
this case. Scientific inquiry requires that any hypothesis
be verified by putting its implications to the test
of actual experience. The difficulty with the "God
hypothesis" is that it is so vague—its object
so "infinitely incomprehensible"—that it
seems to be impossible to draw any definite implications
from its supposed truth. This might appear to fall
short of the demands of pragmatism, but, on closer
look, one finds that after Peirce embraced the reality
of possibility he reconceived the idea of "practical
consequences." In his Harvard Lectures he had
emphasized that the maxim of pragmatism reaches far
beyond the merely practical and allows for any "flight
of imagination," provided only that this imagination
"ultimately alights upon a possible practical
effect." The practical effect that Peirce conceived
the "God hypothesis" to "alight upon"
is "the self-controlled growth of man's conduct
of life." Some scholars wonder whether this weakens
the pragmatic maxim beyond recovery—whether, in other
words, this opens the way for reinstating into our
ontologies all sorts of "beings" that Peirce’s
earlier pragmatism excluded—but that underscores the
fundamental issue raised by this article: whether belief
can have any value for the self-controlled growth of
the conduct of life if its object is not real.
Peirce’s probing of the logic of perception and his
reflections on the effectiveness of religious belief,
probably along with suggestions that arose from his
taxonomic investigations in semiotics, led him in his
last years to devote a great deal of thought to "the
kinds and degrees of assurance that can be afforded
by the different ways of reasoning." The related
theory is what Peirce meant by "logical critics,"
the subject of his intended contribution for a book
to honor Lady Welby. That paper, "A Sketch of
Logical Critics" (sel. 30), is incomplete, but
in the part he finished he made the important point
that by "reasoning" we mean a "change
in thought" that appeals to a relation between
our new cognition (the "conclusion") and
"an already existing cognition" (the premiss
or premisses) to support our assent in the truth of
the conclusion. But not all belief acquisition appeals,
in any deliberate sense, to previous cognition, as
we saw in the case of perceptual judgments and belief
in God. Peirce’s conclusion was that knowledge is acquired
in two ways, by reasoning, of course, but also by experience.
Belief acquired through reasoning must be justified
by what preceded it in our minds, but belief gained
through experience needs no justification.
In the final article in EP2, "An Essay Toward Reasoning
in Security and in Uberty" (sel. 31), Peirce carried
further his consideration of the benefits afforded
by the different kinds of reasoning—although here again
the discussion is left incomplete. This paper, written
in October 1913, only a few months before his death,
might suggest that he was having doubts about the value
of pragmatism. But it would be more accurate to conclude
that in his later years Peirce’s thought gravitated
to ideas and concerns that forced him—or enabled him—to
see the limitations of pragmatism. In 1903 he had proclaimed
Pragmatism to be "a wonderfully efficient instrument
. . . of signal service in every branch of science"
(sel. 10). He had recommended it as advantageous for
the conduct of life. Now he saw that the appeal of
pragmatism was its contribution to the security of
reasoning—but there is a price to pay for security.
According to Peirce, reasoning always involves a trade-off
between security and uberty (rich suggestiveness; potency).
Deductive reasoning provides the most security, but
it is austere and almost entirely without evocative
power. Abduction, on the other hand, is abundant in
its uberty though nearly devoid of security. Peirce
had come to see that pragmatism has the limitations
that come with choosing security over uberty: "[it]
does not bestow a single smile upon beauty, upon moral
virtue, or upon abstract truth;—the three things that
alone raise Humanity above Animality."
Naturalism had grown into a powerful force in Peirce’s
thought. He had come to believe that attunement to
nature was the key to the advancement of knowledge—as
it was for life itself—and he thought that the power
to guess nature's ways was one of the great wonders
of the cosmos. Just as with animals, whose instinct
enables them to "rise far above the general level
of their intelligence" in performing their proper
functions, so it is with humans, whose proper function,
Peirce insisted, is to embody general ideas in art-creations,
in utilities, and above all in theoretical cognition.
But if attunement to nature is the key to the advancement
of knowledge, it is at most a necessary condition;
it puts thought on the scent of truth, which, to attain,
must be won by skilled reasoning. Peirce remained a
logician to the end.
This concludes the thread of development chosen here
to draw together the separate papers in EP2, but it
is only one of many approaches that could have been
taken. Peirce’s shift to a graphical syntax for his
formal logic, with its corresponding emphasis on the
importance of icons for reasoning, led to remarkable
results in logic and in philosophy that parallels the
course of development outlined above. Alternatively,
the evolution of Peirce’s theory of signs that is evident
throughout EP2 might have been more systematically
used to mark movements in Peirce’s thought through
these years. Or one might have expanded on Fisch's
account of Peirce’s ever-strengthening commitment to
realism—or have followed the shifting influence of
major thinkers and scientific discoveries on Peirce’s
thought. These and other approaches could be turned
into useful heuristic guides to Peirce’s intellectual
life in his final two decades. But the growth of his
pragmatism and, in particular, the development of its
proof, surely represents a strong current running through
the period and for much of it probably best represents
Peirce’s leading idea.
Something more should be said about Peirce’s proof of
pragmatism—one of the great puzzles for Peirce scholars.
Max Fisch characterized it as "elusive" and
Richard Robin says it is "unfinished business."(30)
When he first claimed publicly in 1905 to have a proof
(sel. 24), he said it was "a proof which seems
to the writer to leave no reasonable doubt on the subject."
Elsewhere he called it a "strict proof" or
"scientific proof." We should not accept
the pragmatic maxim, Peirce told the auditors of his
second Harvard Lecture (sel. 11), "until it has
passed through the fire of a drastic analysis."
Peirce literally meant to "prove" pragmatism—but
in the sense called for by philosophy. Philosophical
proofs seek to prove truths, not just theorems (they
strive to be sound, not just valid), and must therefore
be concerned with establishing the truth of their premisses.
Only rarely is the deductive form of a philosophical
argument in dispute; the crucial questions almost always
have to do with the legitimacy and strength of the
premisses. And as with science generally, establishing
the relevance and truth of contingent premisses calls
for non-deductive forms of reasoning. As a result,
proving pragmatism calls for marshaling an appropriate
set of assumptions and supportable claims which, as
premisses, will entail pragmatism as expressed in Peirce’s
maxim. In his first Harvard Lecture, to add to the
"strictness" of the proof, Peirce deliberately
expressed his maxim as a theorem: "Pragmatism
is the principle that every theoretical judgment expressible
in a sentence in the indicative mood is a confused
form of thought whose only meaning, if it has any,
lies in its tendency to enforce a corresponding practical
maxim expressible as a conditional sentence having
its apodosis in the imperative mood." So when
Peirce claimed to have a proof of pragmatism, he meant
that he could produce what he believed to be a convincing
rationale, an argument (or, as he would say in his
"Neglected Argument," an argumentation),
to demonstrate that the pragmatic maxim, in a given
form, strictly follows from a given set of premisses,
and, furthermore, that each of the premisses is either
a common assumption or can otherwise be shown to be
admissible.
When Peirce’s efforts to prove pragmatism are understood
to be attempts to provide a convincing rationale or
argument for the truth of his maxim, it makes sense
to suppose that his first proof began to take shape
in the early 1870s when he promoted pragmatism among
the members of the Cambridge Metaphysical Club. His
first published proof, then, would have been the argument
of his "Illustrations." This is the view
expressed by Max Fisch(31) and it is strongly supported
by Peirce himself in his first Harvard Lecture (sel.
10): "The argument upon which I rested the maxim
in my original paper was that belief consists mainly
in being deliberately prepared to adopt the formula
believed in as the guide to action." This belief,
in turn, was carried back to "an original impulse
to act consistently, to have a definite intention."
But this is a "psychological principle" and
by 1903 Peirce no longer thought it "satisfactory
to reduce such fundamental things to psychology."
Besides, as he wrote in the "additament"
to his "Neglected Argument" (sel. 29), "I
must confess the argument . . . might with some justice
be said to beg the question." We might think of
this early proof as the proof based on Peirce’s theory
of belief.
By 1903 Peirce had devoted a great deal of study to
scientific proofs and to epistemic support relationships
across sciences. By then he was much better prepared
to build a proof of pragmatism, and it is clear that
he was thinking of "proof" in a more rigorous
sense. In his more technical restatement of his maxim
for his Harvard Lectures, pragmatism was restricted
to conceptions that can be expressed in sentential
form. According to the pragmatic maxim, so stated,
the meaning of a theoretical judgment expressible in
a sentence in the indicative mood (what was originally
expressed as "the object of our conception")
lies in its tendency to enforce a corresponding practical
maxim that takes the form of a conditional sentence
(originally, "our conception of effects that might
conceivably have practical bearings"). This is
the thesis Peirce set out in 1903 to demonstrate. How
did he go about it? Roughly by establishing, first,
that all intellectual contents amount to theoretical
judgments expressible in indicative sentences and,
second, that all such judgments fundamentally appeal
to imperative practical conditionals. To support the
first part, he established: (1) nothing is in the intellect
that was not first in the senses, (2) the process by
which sensory stimulation rises to perceptual judgment
is not subject to self-control, (3) perceptual judgments
cannot be called into question and are the first premisses
of all our reasonings, (4) perceptual judgments contain
general (i.e. interpretative) elements (as in predicates
of propositions), and (5) although literally particular,
perceptual judgments entail general propositions. Then
Peirce argued that (6) the process which results in
perceptual judgments is a quasi-abductive process (depending
on intellectual habits) which "interprets"
percepts as cases falling under practical conditionals
(and, therefore in relation to a purpose). This effectively
proved his thesis. We might think of this as Peirce’s
proof of pragmatism based on his theory of perception.
In "Pragmatism" (sel. 28), Peirce shifted
the burden of his proof to his theory of signs. He
began by developing his thesis along lines he seemed
to initially have had in mind for his Monist proof
(see selection 26). First he characterized pragmatism
as a method of ascertaining the meaning of "intellectual
concepts" and he noted that "triadic predicates"
are the principal examples (although, in passing, he
considered whether there might be non-intellectual
triadic relations). He noted that while signs can convey
any of three forms of predicates (monadic, dyadic,
or triadic), only triadic predicates are properly called
"intellectual concepts." Only intellectual
concepts convey more than feeling or existential fact,
namely the "would-acts" of habitual behavior;
and no agglomeration of actual happenings can ever
completely fill up the meaning of a "would-be."
This line of thought (with many steps left out) led
Peirce to his thesis, what he called "the kernel
of pragmatism" (p. 402): "The total meaning
of the predication of an intellectual concept consists
in affirming that, under all conceivable circumstances
of a given kind, the subject of the predication would
(or would not) behave in a certain way,—that is, that
it either would, or would not, be true that under given
experiential circumstances (or under a given proportion
of them, taken as they would occur in experience) certain
facts would exist." He also expressed his thesis
in a simpler form: "The whole meaning of an intellectual
predicate is that certain kinds of events would happen,
once in so often, in the course of experience, under
certain kinds of existential circumstances." This
is what Peirce set out to prove in 1907.
Peirce’s proof, much abbreviated, ran something like
this:
1. "Every concept and every thought beyond immediate
perception is a sign."
2. The object of a sign is necessarily unexpressed in
the sign.
3. The interpretant is the "total proper effect
of the sign" and this effect may be emotional,
energetic, or logical, but it is the logical interpretant
alone that constitutes "the intellectual apprehension
of the meaning of a sign."
4. "A sign is anything, of whatsoever mode of being,
which mediates between an object and an interpretant;
since it is both determined by the object relatively
to the interpretant, and determines the interpretant
in reference to the object, in such wise as to cause
the interpretant to be determined by the object through
the mediation of this 'sign.'"
5. The logical interpretant does not correspond to any
kind of object, but is essentially in a relatively
future tense, what Peirce calls a "would-be."
Thus the logical interpretant must be "general
in its possibilities of reference."
6. Therefore, the logical interpretant is of the nature
of habit.
7. A concept, proposition, or argument may be a logical
interpretant, but not a final logical interpretant.
The habit alone, though it may be a sign in some other
way, does not call for further interpretation. It calls
for action.
8. "The deliberately formed, self-analyzing habit
. . . is the living definition, the veritable and final
logical interpretant."
9. "Consequently, the most perfect account of a
concept that words can convey will consist in a description
of that habit which that concept is calculated to produce.
But how otherwise can a habit be described than by
a description of the kind of action to which it gives
rise, with the specification of the conditions and
of the motive?"
This conclusion is virtually a paraphrase of Peirce’s
thesis, the "kernel of pragmatism," so it
completes his proof. We might think of this as the
proof from Peirce’s theory of signs. On 10 April 1907,
Peirce sent Giovanni Papini a similar, though somewhat
fuller, outline and explained that "among all
scientific proofs with which I am acquainted [this
is] the one that seems to me to come nearest to popular
apprehension."(32)
When Peirce began his third Monist series, represented
in EP2 in selections 24-27, he probably had something
like the above proof in mind, although perhaps something
more wide-ranging. The definition of pragmatism as
set out in "What Pragmatism Is" (sel. 24)
gives some idea of what he was aiming for: pragmatism,
he wrote, is "the theory that a conception, that
is, the rational purport of a word or other expression,
lies exclusively in its conceivable bearing upon the
conduct of life; so that, since obviously nothing that
might not result from experiment can have any direct
bearing upon conduct, if one can define accurately
all the conceivable experimental phenomena which the
affirmation or denial of a concept could imply, one
will have therein a complete definition of the concept,
and there is absolutely nothing more in it" (332).
Peirce pointed out that to prove this thesis it would
be necessary to appeal to a wide range of "preliminary
propositions." Don D. Roberts has listed seventeen
"premisses" that he thinks are likely to
be among the ones Peirce had in mind, and these include
"dismiss make-believes," "logical self-control
is a mirror of ethical self-control," "an
experiment is an operation of thought," "we
do not doubt that we can exert a measure of self-control
over our future actions," "a person is not
absolutely individual," and "thinking is
a kind of dialogue."(33)
Midway through his third Monist series, Peirce changed
his mind and decided to base his proof on his Existential
Graphs. He never completed his graph-based proof, but
there are many manuscript pages indicating what he
had in mind. In one draft (MS 298) Peirce explained:
"You 'catch on,' I hope. I mean, you apprehend
in what way the system of Existential Graphs is to
furnish a test of the truth or falsity of Pragmaticism.
Namely, a sufficient study of the Graphs should show
what nature is truly common to all significations of
concepts; whereupon a comparison will show whether
that nature be or be not the very ilk that Pragmaticism
(by the definition of it) avers that it is. . . ."
That proof, as represented in preliminary form in Peirce’s
1906 "Prolegomena to an Apology for Pragmaticism"
(CP 4.530-72) and in MSS 296-300, is extremely complex.
It depends heavily on establishing that the system
of Existential Graphs provides a working model of thought
and that experimenting with the Graphs amounts to experimenting
with concepts themselves. The sweep of issues addressed
in the premisses of this proof includes: that the proper
objects for investigation in experiments with diagrams
are forms of relation; that deductive reasoning is
no more certain than inductive reasoning when experimentation
can be "multiplied at will at no more cost than
a summons before the imagination"; that icons
have more to do with the living character of truth
than either symbols or indices; that reasoning must
be chiefly concerned with forms; that diagrams are
icons of the forms of relations that constitute their
objects; that members of a collection, taken singly,
are not as numerous as the relations among them; that
there can be no thought without signs and there are
no isolated signs; that every logical evolution of
thought should be dialogic; and that thought is not
necessarily connected with a brain. This is only a
sampling. There is little doubt that the full exposition
of Peirce’s Graphs-based proof would shed considerable
light on the complex network of relationships internal
to Peirce’s system of thought that support pragmatism,
but it is not so clear whether its upshot would be
to prove pragmatism or to prove that the system of
Existential Graphs is a valid normative logic of cognition—really
a "moving picture of thought" as Peirce once
said (CP 4.11).
Most of Peirce’s arguments for pragmatism, and there
are a number that have not been mentioned, seem to
be quite straightforward in setting out what is to
be proved—the pragmatic maxim as a carefully stated
thesis—and in supplying the assumptions and premisses
that entail that thesis as conclusion. The intractibility
of these arguments usually results from their large
number of premisses, ranging over vast sweeps of Peirce’s
system of thought, and from the difficulty involved
in establishing the premisses. But the matter is complicated
by the fact that many of the involved premisses require
inductive support, and by apparent promises of inductive
confirmation for the pragmatic conclusion, which Peirce
thought his readers might hesitate to accept because
of the overall complexity of the argument and the novel
ideas it involved.(34) An important question emerges:
What kind of principle is the pragmatic maxim after
all? Is it a logical maxim and a regulative principle,
or is it a positive truth that can be treated as a
scientific hypothesis calling for inductive confirmation?
Peirce’s treatment suggests that it is both. But as
a positive truth informing us how to construe the meaning
of conceptions or propositions—signs with intellectual
value—how could the pragmatic maxim be confirmed? In
criticizing the argument of his 1877-78 "Illustrations,"
Peirce disallowed any appeal to psychology, and in
any case his classification of the sciences shows that
the only positive sciences that can legitimately be
appealed to are phenomenology and the prior normative
sciences (and parts of logic) on which logical methods
must rely. Peirce thought the maxim could be tested
by using it to analyze familiar intellectual conceptions
such as "real," "identity," "sequence,"
"substance," "time," and "probability,"
but only after he had established that his logical
analyses of those conceptions was neither psychological
nor question-begging. That seems to be why he had first
to prove that working with his Existential Graphs was
"equivalent" to working with conceptions
themselves. His proof from the Existential Graphs,
then, appears to have been integral to his effort to
prove pragmatism inductively. One of the limitations
of this approach is that it can never wield demonstrative
force, and the argument can always be carried further;
but the hope must be that the time will come when further
confirmation is beside the point. It is probably this
inductive approach that has lent support to the view
that Peirce’s proof is rather amorphous and perhaps
at best a cable with fibers of independent sub-arguments.
Overall, it is easy to see why Thompson said that a
"real proof" of pragmatism "would amount
to a kind of elucidation of most of Peirce’s philosophy
and formal logic" and why Robin said that "coming
to terms with pragmatism's proof" means coming
to terms "with the whole Peirce."(35)
When Peirce died in the spring of 1914 he left a lot
of important work unfinished. Perhaps most to be regretted
is that he was unable to complete his "System
of Logic, Considered as Semeiotic," which he hoped
would stand for realism in the twentieth century as
Mill's System of Logic had stood for nominalism in
the nineteenth.(36) As it was, he did leave far more
than has since been put to good use. More than fifty
years ago, the great American social philosopher, Sidney
Hook, wrote of Peirce that "he is just as much
the philosopher's philosopher [today], just as much
the pioneer of a second Copernican revolution in thought
(one more genuine than Kant's) as he was when his meteoric
genius first flashed across American skies."(37)
It is still true that Peirce is mainly a "philosopher's
philosopher." But it may turn out that his pioneering
work, perhaps especially his later writings so tightly
packed with ideas, will bloom at last into the influential
legacy that Peirce in hopeful moments imagined would
be his bequest to the future. Perhaps this collection,
in spite of its limitations, will contribute to that
end.
Nathan Houser
1. See Max H. Fisch, Peirce, Semeiotic, and Pragmatism, K. L. Ketner and C. J. W. Kloesel, eds. (Indiana University Press, 1986), pp. 227-48.
2. Murray G. Murphey, The Development of Peirce’s Philosophy (Harvard University Press, 1961; Indianapolis: Hackett Publishing Co., 1993), p. 3.
3. Peirce’s life was long neglected and is still obscure. The best accounts can be found in: Fisch, Peirce, Semeiotic, and Pragmatism; Joseph Brent, Charles Sanders Peirce: A Life (Indiana University Press, 1993; revised ed. 1998); and Kenneth Laine Ketner, His Glassy Essence: An Autobiography of Charles Sanders Peirce (Vanderbilt University Press, 1998).
4. Harold Henderson, Catalyst for Controversy: Paul Carus of Open Court, (Southern Illinois University Press, 1993). The Open Court Publishing Company was owned by the Chicago industrialist Edward C. Hegeler.
5. Fisch, Peirce, Semeiotic, and Pragmatism, p. 193
6. Peirce’s book was completed but not published in his lifetime. See notes 2-4 to selection 22 (p. 537).
7. Peirce’s reviews appeared in the Nation and the Monist; see P620 (CP 3.425-455), P627 (CN 2:132-33), and P637 (CP 3.456-552).
8. Fisch, Peirce, Semeiotic, and Pragmatism, p. 194.
9. This and the quotations that follow in this paragraph are from the opening essay of William James, The Will to Believe and Other Essays in Popular Philosophy (Longmans Green, 1896; Harvard University Press, 1979).
10. For Fisch's full account see Peirce, Semeiotic, and Pragmatism, pp. 283 ff.
11. K. L. Ketner and H. Putnam speculate that James's new-found interest in pragmatism, as well as "Royce's drift toward Peirce’s ideas," was a consequence of Peirce’s 1898 Cambridge Lectures (RLT 36).
12. Peirce’s key anti-foundational arguments had appeared earlier in his 1868 Journal of Speculative Philosophy series; EP1, selections 2-4.
13. According to Murray Murphey, James's lecture put Peirce "in an intolerable intellectual position." Peirce could not now disown pragmatism, but neither could he "embrace it without qualification." Peirce had to come forward with his distinct views (The Development of Peirce’s Philosophy, pp. 358-59).
14. See Brent, Charles Sanders Peirce: A Life, ch. 4.
15. Quoted in Eisele's NEM 3:780.
16. This article, as reprinted in the Annual Report of the Smithsonian Institution for Year Ending June 30, 1900 (Washington, D.C., 1901) is published in Philip P. Wiener, ed., Charles S. Peirce: Selected Writings (Dover, 1966), pp. 265-74. Quotations are taken from Wiener's book.
17. Fisch, Peirce, Semeiotic, and Pragmatism, p. 334
18. For an illustration of the logical depth of Peirce’s work for this book, see the chapters by Glenn Clark and Shea Zellweger in Studies in the Logic of Charles Sanders Peirce (Indiana University Press, 1997).
19. Peirce’s application to the Carnegie Institution (L 75) is available electronically on the Peirce-focused website.
20. Fisch, Peirce, Semeiotic, and Pragmatism, p. 195.
21. Fisch, Peirce, Semeiotic, and Pragmatism, p. 365.
22. Fisch, Peirce, Semeiotic, and Pragmatism, p. 195.
23. See Fisch, Peirce, Semeiotic, and Pragmatism, p. 365 and Richard S. Robin, "Classical Pragmatism and Pragmatism's Proof" in The Rule of Reason: The Philosophy of Charles Sanders Peirce, Jacqueline Brunning and Paul Forster, eds. (University of Toronto Press, 1997), p. 149.
24. Fisch, Peirce, Semeiotic, and Pragmatism, p. 196.
25. See Fisch, "Peirce’s Triadic Logic" (written with Atwell Turquette) in Peirce, Semeiotic, and Pragmatism, pp. 171-83, for details and for further remarks on triadic logic.
26. Fisch, Peirce, Semeiotic, and Pragmatism, p. 196.
27. According to Fisch (Peirce, Semeiotic, and Pragmatism, p. 196), material (Philonian) implication was Peirce’s last nominalist stronghold.
28. James Jakób Liszka, A General Introduction to the Semeiotic of Charles Sanders Peirce (Indiana University Press, 1996).
29. Peirce to C. J. Keyser, 10 April 1908 (Rare Book and Manuscript Library, Columbia University).
30. Fisch, Peirce, Semeiotic, and Pragmatism, p. 363, and Robin, "Classical Pragmatism and Pragmatism's Proof," p. 149.
31. Fisch, Peirce, Semeiotic, and Pragmatism, p. 363.
32. Peirce to G. Papini, 10 April 1907 (Papini Archives).
33.Don D. Roberts, "An Introduction to Peirce’s Proof of Pragmatism," Transactions of the Charles S. Peirce Society 14 (1978), p. 128.
34. See, for example, MS 300 and Roberts, "An Introduction to Peirce’s Proof of Pragmatism," p. 129, for some elaboration.
35. Manley Thompson, The Pragmatic Philosophy of C. S. Peirce (University of Chicago Press, 1953), p. 249. Robin, "Classical Pragmatism and Pragmatism's Proof," p. 150.
36. See MS 640 and NEM 3:875; and Fisch, Peirce, Semeiotic, and Pragmatism, p. 196. Many manuscripts from Peirce’s last decade develop logic from the standpoint of semiotics but, perhaps, none more fully than MS 693.
37. Quoted from a tribute solicited by Frederic Harold Young and published by him in Charles Sanders Peirce; America's Greatest Logician and Most Original Philosopher (privately published, 1946), an address delivered in October 1945 to the Pike County Historical Society in Milford, Pennsylvania.
The caret (^) stands for missing punctuation; the tilde (~) represents an unchanged word adjacent to variant punctuation. Line numbering within footnotes take the form “fn l. #"; within selection headnotes they take the form “hn #”.
| PAGE #.LINE # | ERROR | CORRECTION |
|---|---|---|
| v.1 | question^ | ~ ; |
| v.2 | eye^ | ~ , |
| viii.19–20 | An Essay toward Reasoning in Security and Uberty | An Essay toward Improving Our Reasoning in Security and in Uberty |
| ix.5 | aid | aide |
| ix.19 | 1 Dec. | 1 July ’67 [1 Dec.] line to be moved after l. 12 in Chronology |
| ix.36 | 30 Apr. | 26 Apr. |
| ix.41 | 5,000 | 15,000 |
| x.28 | 26 Mar. | 26 Mar. |
| xxxvii.16 | support | supports |
| 10.17 | ^ In | §9. In |
| 10.28 | §9. Suppose | ^ Suppose |
| 37.2 | meterology | meteorology (See explanation below under H) |
| 67.11 | observations^ | ~ , |
| 107.12 | able^ | ~ , |
| 117.30-31 (margin) | Distributio of characti | Distribution of characters |
| 134.43 | the form | the same form |
| 138.20 | time^ | ~ , |
| 146.38 | a very | [a] very |
| 155.42 | Cantor, | ~ ^ |
| 155.42 | like^ | ~ , |
| 177.5 | exercize | exercise |
| 180.7 | doctrine of | doctrine [of] |
| 185.15-16 | where ( | (where |
| 197.34 | philosophy | Philosophy |
| 219.10 | being | [being] |
| 222.13 | [an] | [an] |
| 226 hn 1 | 241–56). | 241–56. |
| 231.13–15 | No doubt in regard to . . . mistaken for perceptions. | See discussion of this problematic sentence below this table. |
| 240.13 | qualified, | qualified |
| 242 hn 1 | (MS 440) | (MS 448) |
| 242 hn 1 | 7.611 | 1.611 |
| 256.9 | himself to, | himself, |
| 280 fn l. 8 | not sit | non sit |
| 283.23 | dicisigns | Dicisigns |
| 285 fn l. 1 | κατηγορεύμενον | κατηγορούμενον |
| 290.8–13 | The First Correlate . . . of that nature. ¶The Third Correlate … of that nature. | See discussion of these two problematic sentences below this table. |
| 303.12 | which states [that] what it will be sufficient to show must, in every case, be true concerning the diagram. | which states what it will be sufficient to show must, in every case, be true concerning the diagram. (See discussion below) |
| 319.26 | as | us |
| 344.29–30 | the two of one pair being convertible into [one] another | the two of one pair being convertible into another (See discussion below) |
| 346.2 | bearings^ | ~ , |
| 346.3 | the effects | those effects |
| 355.11 | since you are both certain | 2 possible corrections: since we are both certain since you and I are both certain |
| 357.42 | indispensible | indispensable |
| 371.5 | 5.449-54 | 5.549-54 |
| 392.16–17 | a determination of the contents of the first bottle’s contents | a determination of the contents of the first bottle |
| 393.35 | meaning | meanings |
| 401.13 | there certainly appears to be no slight | there is certainly a slight |
| 426.18 | millions of millions or millions | millions of millions of millions |
| 434.7 | Plato’s ideas | Plato’s idea |
| 435-449 (header) | The Neglected | A Neglected |
| 479.25 | Facts | facts |
| 479.28 | Facts. | Facts. |
| 481 fn l. 1 | ὁμοιωμάτα | ὁμοίωματα |
| 495.30 | [the] | [the] |
| 506.0 (header) | pages 36-40 | pages 35-40 |
| 507.18 | chapters 13 | chapters 1-3 |
| 516 ann. 18 l. 3 | proved in 1996. | proved by Andrew Wiles in 1993. |
| 517.23 | misssed | missed |
| 519.9 | See note above | See note 1 above |
| 519 ann. 29 | Rudolf Clausius stated in 1850 the first law of thermodynamics, | Julius Robert von Mayer in 1842, and James Prescott Joule and Hermann von Helmholz in 1847 stated the first law of thermodynamics, |
| 546 ann. 7 l. 2 | see W2: 14–60, | see W3: 14–60, |
| 550 ann. 8 | Critique of Pure Reason, A154–58, B193–97. | Critique of Pure Reason, A7, 303–5; B11, 360–61. |
| 551 ann. 14 l. 7 | wich | which |
| 554 ann. 10 l. 2 | subtitly | subtilty |
| 555 ann. 4 l. 1 | in the margin. | in the bottom margin. |
| 560.1.51 | xxx; | ~ , |
| 569 c. 1 l. 55 | Jacks, L. P. | Jacks, Lawrence Pearsall |
| 579 c. 1 l. 1 | Representamen | Representation |
| 581 c. 2 l. 8 | Sphinx, 509n9 (2) | Delete this index entry. |
That sentence reads as follows in EP2: 231:
No doubt in regard to the first cotary proposition follows as a necessary consequence of the possibility that what are really abductions have been mistaken for perceptions.
The sentence as given is a syntactically correct reconstruction—when one understands “No doubt” to be the subject of “follows”—of a passage that underwent two layers of alterations by Peirce. Interestingly, the solution offered by EP2 differs from the solution given by the Collected Papers editors in CP 5.188, which ran as follows:
No doubt, in regard to the first cotary proposition, [that proposition] follows as a necessary consequence of the possibility that what are really abductions have been mistaken for perceptions.
The CP editors added commas around the clause “in regard to the first cotary proposition”, and, interpreting “No doubt” as an adverbial phrase equivalent to “Without doubt,” they added a new bracketed subject, “[that proposition],” to the verb “follows.” The problem this syntactical solution created was the implication that the first cotary proposition was a necessary consequence of the possibility that what are really abductions have been mistaken for perceptions. The first cotary proposition is Nihil est in intellectu quin prius fuerit in sensu—by which Peirce means that nothing is part of the meaning of any representation in any kind of cognition which was not first given in a perceptual judgment as the starting-point or first premise of all critical and controlled thinking (EP2: 226–27). How could the primacy of perceptions follow necessarily from a non-cotary proposition according to which there are real abductions that are not perceptions?
The entire ambiguity comes from the two words starting the sentence, “No doubt”. In the original manuscript of the lecture (Harvard Lecture VII), R 315: ISP 17, the sentence was first inscribed as follows, directly after the two previous sentences (“It may therefore very likely be objected that doubt must perforce on this account hang over my first cotary proposition that every general element of thought is given in perceptive judgment. This objection, however, involves a logical fallacy.”):
There is no such doubt
Peirce then immediately altered this sentence opening by deleting “There is” and capitalizing ”no” into “No”. This gave the reading:
No such doubt
And Peirce continued writing:
No such doubt follows as a necessary consequence of the possibility that abductions are mistaken for perceptions.
When Peirce revised the lecture in part to shorten it for public delivery because it was too long, he decided to skip a large section of text that directly preceded the “No such doubt” sentence, from EP2: 230 line 23 (“At the same time”) to 231 line 13 “a logical fallacy.” He replaced that passage with the following two sentences:
I should easily show you that this difficulty, however formidable theoretically, amounts practically to little or nothing for a person skilled in shaping such inquiries. But this is unnecessary, since the objection founded upon it has no logical force, whatever.
This replacement forced Peirce to return to the “No such doubt” sentence and to alter it furthermore. To begin with, he deleted the predeterminer “such” because the antecedent to it (the penultimate sentence of the skipped passage beginning with “It may therefore very likely be objected that doubt must perforce”) was no longer present. By reason of that absence, too, Peirce then inserted the clause “in regard to the first cotary proposition” before “follows” (a verb which he mistakenly deleted and then reinstated). Those edits resulted in a new reading:
No doubt in regard to the first cotary proposition follows as a necessary consequence of the possibility that abductions are mistaken for perceptions.
But since the matter of abductions being mistaken for perceptions had been broached at the beginning of the second skipped paragraph in the present tense, and that those lines had now been abandoned, Peirce also altered the ending of the sentence so that “abductions are mistaken for perceptions” became “what are really abductions have been mistaken for perceptions.”
It therefore appears that when EP2 editors decided to restore the skipped passage, a complete restoration should have yielded either the following reading (= Peirce’s original reading) or the next one if one thought the changes made to the end of the sentence had occurred during its initial jotting:
No such doubt follows as a necessary consequence of the possibility that abductions are mistaken for perceptions.
No such doubt follows as a necessary consequence of the possibility that what are really abductions have been mistaken for perceptions.
The minimal correction to the sentence in EP2 therefore involves inserting “such” before “doubt” and deleting the redundant addition “in regard to the first cotary proposition”. The maximal correction involves in addition deleting the words “what are really” and replacing “have been” with “are” at the end of the sentence.
The error here reported was first signaled by the Collected Papers editors in CP 2.235*–236*. Peirce wrote the two sentences just as published in EP2:
The First Correlate is that one of the three which is regarded as of the simplest nature, being a mere possibility if any one of the three is of that nature, and not being a law unless all three are of that nature.
The Third Correlate is that one of the three which is regarded as of the most complex nature, being a law if any one of the three is a law, and not being a mere possibility unless all three are of that nature.
The correction consists in transposing the second clause of each sentence with each other, as follows:
The First Correlate is that one of the three which is regarded as of the simplest nature, being a law if any one of the three is a law, and not being a mere possibility unless all three are of that nature.
The Third Correlate is that one of the three which is regarded as of the most complex nature, being a mere possibility if any one of the three is of that nature, and not being a law unless all three are of that nature.
The explanation comes from looking at the table of the ten trichotomies involving three correlates, where P = Possibility = 1, E = Existent = 2, and L = Law = 3.It is clear that the first correlate is a P or mere possibility only and only if “all three are of that nature” (PPP), and it happens to be an L whenever there is an L in the trichotomy.
It is also clear that the third correlate happens to be a P or mere possibility whenever there is a P in the trichotomy, and is an L or law only when all three are L (LLL).
In the manuscript page corresponding to EP2: 303.11–13 Peirce wrote:
Then comes, third, the ecthesis, which states what it will be sufficient to show must, in every case, be true concerning the diagram.
EP2 editors added [that] after the verb “states”, but this altered the meaning of the sentence by making the clause “what it will be sufficient to show” the subject of “must be true”—thereby also making “what” the object of “to show” independently of the modal phrase “must be true”. But Peirce merely meant that subject to be confined to the pronoun “what”, thus shifting the object of “to show” to the necessity embedded in “must be true”: the ecthesis need only state what must, in every case, be true concerning the diagram.
Worth noting in passing is that Peirce may be representing the structure of a Euclidean demonstration following Proclus’s description of it. If so, what Peirce calls precept in the paragraph is actually the ekthesis (“setting out”: “Let A be a line etc.”) akin to a universal instantiation of the conditional part of the protasis (“general enunciation” in Peirce’s words). What he calls an “ecthesis” is actually what should be called the diorismos (a universal instantiation of the consequence expressed in the protasis). The “subsidiary construction” is the kataskeue; the “demonstration” is the apodeixis; and the statement involving the Q.E.D. is the superasma. See Reviel Netz, “Proclus’ Division of the Mathematical Proposition into Parts: How and Why Was It Formulated?” in The Classical Quarterly, 49.1 (1999): 282–303, especially 284–85.
The sentence at EP2: 344.29–30 reads as follows:
Now, it is well known that propositions in formal logic go in pairs, the two of one pair being converted into [one] another by the interchange of the ideas of antecedent and consequent, subject and predicate, etc.
In April 2008, Daniel Kruidenier, then a former graduate student in philosophy at Indiana University Indianapolis, questioned the editorial insertion of “[one]”. Why did EP2 editors take such a liberty? The first reason was born out of a syntactical concern: the subject of the verb “being converted” is plural, for it refers to two propositions. Those two propositions are converted into “another” what? Another “two propositions”? It makes syntactical sense to say that one pair is converted into another pair, as pair. But Peirce is not saying that the pair is being converted into another pair, but it is the two propositions that are being converted so as to form another pair, through a process that involves interchange of subjects with predicates and antecedents with consequents. The pair as such is not predicated or conditionalized, but the propositions that constitute it are. It follows that the interchange occurs between the two propositions themselves. One would thus surmise that the two propositions are converted into one another through such an interchange, and that the result will indeed provide a new pair. Therefore inserting “[one]” appears to usefully disambiguate the sentence. The second argument that buttresses this correction comes from the draft version of that sentence. The draft of the text “What Pragmatism Is” is in R 329. Page R 329 ISP 63 is the draft of the text in EP2: 344. And there, in Peirce’s hand, what do we read? ... “the two of one pair being convertible into one another by the interchange of the ideas of antecedent and consequent, subject and predicate, etc.” That was the authoritative source for the correction in EP2.
But this in itself is not sufficient as an argument for one might object that in rewriting that sentence Peirce intentionally removed the “one” because he found it to be mistaken. To figure this out, one must take into account the context, which is all important. What Peirce does in the full paragraph containing the problematic sentence is first to provide his own augmented translation of Aristotle’s Dictum de omni that defines what is a universal predication, whether affirmative (“All”) or negative (“None”). A more literal translation of Aristotle’s definition (Prior Analytics 24b28-30 [= end of section 1 of book I]) goes like this:
And we say that a term is predicated of ‘all’ of something whenever nothing among what belongs to the subject can be found of which the predicate term cannot be asserted; and similarly in the case regarding ‘none’.
Peirce’s translation in EP2: 344 (which see) incorporates the above sentence’s second clause regarding the universal negative within the first clause, clarifying through inserted parentheses that the definition applies to both affirmative and negative universals. Peirce’s translation in that respect is quite original. What he does next is to use a principle of convertibility in order to construct, on the basis of his translation, another logical principle that defines an affirmative predication (which could be called his Dictum de adfirmatione). The construction of that new principle involves the interchange (or swapping or substitution) of several subjects and predicates within his translation. (Worth noting is that section 2 and 3 of Prior Analytics 25a1 to 25b26 discusses syllogistic conditions under which such conversions can take place.)
How does Peirce convert the Dictum de omni? Let’s first notice that that Dictum actually consists of a pair of propositions: one that speaks about an affirmative universal predication, and the other (known as Dictum de nullo) about a negative universal predication. Let’s also notice that Peirce makes explicit Aristotle’s implicit appeal to particular instances of a universal (“existent individuals”). The predicates at play include therefore “universal,” “particular,” “affirmative,” “negative,” while the subject instances at play include “existent individuals” and “sensational effects.” What Peirce does is to convert “universal” into “affirmative” (and vice versa), and “particular” into “negative” (and vice versa). Since affirmation is about attributing either the total set or a partial set of whatever effects are entailed by a predicate to a subject, the stakes of the conversion concern the comprehension or intension of the predicate in terms of its range of applicability, and thus for instance the range of its instantiation into various sensational effects. Peirce accordingly replaces “existent individuals” (members of the universal’s extension as particular instances of it) with “sensational effects” (as full or partial connotations of the affirmed predicate’s intension).
The result yields a new pair of propositions (one about universal affirmative predications and the other about particular affirmative predications) — Peirce’s Dictum de adfirmatione, which, he intimates, is equivalent to the pragmatic maxim. He calls this second Dictum the “mate” of the first. Thus the second pair of propositions was born from the first pair of propositions by interchanging predicates and subjects that were all available, explicitly or implicitly, within the first pair of propositions.
Can it be maintained, however, that the interchange occurred between the affirmative universal version of the Dictum de omni and its negative version? No, for it is not the case that one got converted into the other. It is more the case that both propositions got converted at once through the same substitutional formula. It follows that the editors of EP2 did not need to add “[one]” to Peirce’s sentence. It would have been preferable to add “[pair]” after Peirce’s “another”, if Peirce’s own application of the adduced conversion principle is a legitimate guide.
One more remark. If the Dictum de omni is paired with the Dictum de nullo, what should the Dictum de adfirmatione be paired with? Not exactly with a Dictum de negatione, for that would be too ambiguous: negating a predicate is tantamount to affirming its negative form. Peirce’s pragmatic Dictum targets the range of meaning of a conception, preferably the “whole” range of its conceivable practical effects. A universal affirmation affirms that the entire set of sensational effects conceivably comprehended within a predicate term applies to the predicated subject. The negation of that universal affirmation is only its particularization or partialization; what gets affirmed is not the full range of conceivable consequences but a partial range. Hence the counterpart to the Dictum de adfirmatione could be called the Dictum de limitatione.
One may therefore conclude that in EP2: 344 Peirce converted the Dictum de omni et nullo into the Dictum de adfirmatione et limitatione.
The author of the French witticism (EP2: 34.3–5) here translated appears to be the Marquis d’Argenson, according to a possible source: Encyclopédiana. Recueil d’anecdotes anciennes et modernes et contemporaines tirées de tous les recueils de ce genre publiés jusqu’à ce jour; de tous les livres rares et curieux touchant les mœurs et les usages des peuples; ou de la vie des hommes illustres. Paris: J. Laisné, 1842, nouvelle série, p. 427. Which Marquis d’Argenson, though? That is difficult to determine. It could have been René Louis de Voyer de Paulmy, marquis d’Argenson (1694–1757), friend of Voltaire, but he did not live under the Reign of Terror (as Peirce surmises the witticism’s author did, without traceable foundation). Or it could have been Marc-René de Voyer de Paulmy d'Argenson (1771–1842), the kind of character who could have uttered that very kind of witticism.
Hegel’s “three stages of thought” do not consist of thesis, antithesis, and synthesis, but of naïve acceptance, reaction and criticism, and rational conviction, as Peirce put it in CP 8.45.
EP2: 50 ll. 1–2 read as follows: “Stones do not fall from heaven” said Laplace,
Laplace does not appear to have said any such thing. This is likely an allusion to a report of the French Académie des Sciences reporting that a stone that fell in September 1768 in Lucé (Sarthe) did not fall from the sky (“La pierre ne doit point son origine au tonnerre… Elle n’est pas tombée du ciel.”) The report, dated 1772 and published in 1777 in volume 2 of the Journal de la Physique (pp. 252–255), was signed by several chemists: Fourgeroux, Cadet, and Lavoisier. The latter is reported to have declared, during a session of the French Academy of Sciences, that reports about aerolites were fables: “Il ne peut pas tomber des pierres du ciel, par la bonne raison qu’il n’y a pas de pierres dans le ciel” (La Grande Encyclopédie, Inventaire raisonné des sciences, des lettres et des arts, volume XXV, entry "Paradoxe," p. 1010, n.d.). In R 882: 3 (1895), Peirce erroneously attributed this claim to Jean-André DeLuc, a Swiss geologist and meteorologist (1727–1817); it was rather the latter’s younger brother Guillaume-Antoine DeLuc (1729–1812) who made such representations in an epistolary debate (in Bibliothèque Britannique and in Journal des Mines, 1801–1802) opposing him to Marc-Auguste Pictet. See Ursula B. Marvin, “Ernst Florens Friedrich Chladni (1756–1827) and the origins of modern meteorite research” in Meteoritics & Planetary Science 31.5 (1996): 545–88, especially p. 555 regarding Lavoisier and 565–67 & 569 regarding DeLuc.
Peirce hastily inscribed and thus miswrote the word “meteorology” in the manuscript (R 437), where it more or less reads like “meteolorogy”. The word was transcribed as “metrology” in RLT 117 l. 6. The erroneous reading “meterology” in EP2: 37 resulted from an ill-conducted transpositional emendation. Peirce lists meteorology as one of the physical sciences in W8: 275.
“Our Aristotle abounds in references to his own works, sometimes to lost works, but mostly apparently to the works we know under other titles, but the nomenclature of the titles in the references presents no fixity; the same work will receive from Aristotle himself various names,—unless he means to refer to some works that we do not know.”
The following system of references is used in this website, in The Essential Peirce, and in the Writings of Charles S. Peirce.
The Century Dictionary and Cyclopedia, 10 vols., ed. William D. Whitney (New York: The Century Company, 1889–91). The pagination is that of Peirce’s personal interleaved copy, which was the dictionary’s first printing. Unless specified otherwise all quotations of definitions with a CD citation are considered Peirce’s and were marked by him in his personal copy.
Any Peirce document listed in the Chronological Catalog published in Writings of Charles S. Peirce, beginning with volume 6 (W6). Catalog numbering restarts at 1 each time a new year or circa year is reached. This practice yields a flexible reference and filing system that allows users to refer to any document by its year and sequence number: CH 1890.18 or CH c. 1891.6, for example. The letters CH are optional.
Chance, Love, and Logic: Philosophical Essays, by the Late Charles S. Peirce, ed. Morris R. Cohen (New York: Harcourt, Brace & Company, 1923).
Contributions to The Nation, 4 parts, ed. Kenneth L. Ketner and James E. Cook (Lubbock: Texas Tech Press, 1975–1988). A searchable CD-ROM edition is published by InteLex Corporation (1999) as part of Charles Sanders Peirce: Published Philosophy (I).
Collected Papers of Charles Sanders Peirce, volumes 1–6, ed. Charles Hartshorne and Paul Weiss; volumes 7–8, ed. Arthur Burks (Cambridge: Harvard University Press, 1932–35, 1958).
Robinson, Stetson J. The Correspondence of Charles S. Peirce and the Open Court Publishing Company, 1890–1913 (Berlin, Boston: De Gruyter, vol. 5 in Peirceana series, 2022). https://doi.org/10.1515/9783110768756
The Essential Peirce, volume 1 ed. Nathan Houser and Christian Kloesel; volume 2 ed. Peirce Edition Project (Bloomington, IN: Indiana University Press, 1992, 1998).
The Nation: Indexes of Titles and Contributors (volumes 1–105: 1865–1917), 2 vols., comp. Daniel C. Haskell (New York: New York Public Library, 1951, 1953). Volume 1, Index of Titles, is arranged chronologically, by volume and page number, and includes attribution. Signed publications are not included in this volume. Volume 2, Index of Contributors, is arranged alphabetically by author, and includes both signed and unsigned publications. In volume 2, Peirce’s contributions are listed on pages 392 to 395. Neither volume includes unattributed publications.
Historical Perspectives on Peirce’s Logic of Science, 2 vols., ed. Carolyn Eisele (New York: Mouton, 1985).
A combined number consisting of the Robin catalogue number and a sequential sheet number. The numbers were Bates-stamped in 1974 on each sheet of an electroprint copy made from The Charles S. Peirce Papers (Cambridge: Harvard University Library, 1966, 33 reels including supplement) and kept at the Institute for Studies in Pragmaticism, at Teas Tech University, Lubbock. The ISP numbers give each page a unique identifier and with some exceptions the numbering follows closely the order of the pages on the microfilm. Harvard documents that were not microfilmed, such as those in R 1600 and RL 100, do not have ISP numbers, neither do documents held elsewhere.
National Archives Record Group
New Elements of Mathematics, 4 vols. in 5, ed. Carolyn Eisele (The Hague: Mouton, 1976).
A publication by someone other than Peirce listed in A Comprehensive Bibliography of the Published Works of Charles Sanders Peirce, 2nd edition rev., ed. Kenneth L. Ketner (Bowling Green: Philosophy Documentation Center, 1986).
A Peirce publication listed in A Comprehensive Bibliography.
Philosophical Writings of Peirce, ed. Justus Buchler (New York: Dover 1955), previously published as The Philosophy of Peirce: Selected Writings (New York: Routledge and Kegan Paul, 1940).
A Harvard manuscript listed in Richard S. Robin’s Annotated Catalogue of the Papers of Charles S. Peirce (Amherst: University of Massachusetts Press, 1967). Numbers preceded by RL refer to letters that are listed in the correspondence section of Robin’s catalogue. Numbers preceded by RS are listed in Robin’s “The Peirce Papers: A Supplementary Catalogue” (Transactions of the Charles S. Peirce Society 7 [1971]: 37–57).
Reasoning and the Logic of Things, ed. Kenneth L. Ketner (Cambridge: Harvard University Press, 1992).
Values in a Universe of Chance, ed. Philip P. Wiener (Garden City: Doubleday, 1958). Later published as Charles S. Peirce: Selected Writings (New York: Dover, 1966).
Writings of Charles S. Peirce (Bloomington, IN: Indiana University Press, 1982–).
A Peirce manuscript listed in the Chronological List published in W1–W5.
“Have a pad always about you, and note upon one of them anything worthy of note, the subject being stated at the top and reference being made below to available books or to your own note books.”